Коньюнктор.
|
|
|
|
 (На какой вход необходимо подать сигнал, чтобы сигнал
(На какой вход необходимо подать сигнал, чтобы сигнал был А
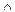 В?)
В?)
 | |||
 |
+
Пример: Гирлянда.
1) Если 1 лампочка не горит, то нет выходного сигнала).
2) В метро, пока все двери не закрыты, машинист не получит сигнал).
2. Дизъюнкция или логическое сложение – это объединение двух простых высказываний А и В в одно составное с помощью союза <или>. Составное высказывание будет истинно, если истинно хотя бы одно из входящих в него простых высказываний.
Обозначение:
А+В, А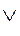 В(или), А or В(логическая связка), А
В(или), А or В(логическая связка), А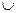 В(объединение)
В(объединение)
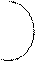


в теории множеств
Таблица истинности.
| А | В | А В В
|
| 0 0 |
Реализация логического сложения - дизъюнктор.

(Параллельное соединение, пожарная сигнализация).
3. Инверсия – логическое отрицание – это присоединение частицы не или словосочетания не верно, что к высказыванию А.
(Сейчас идет урок. Проанализируйте. Сейчас не идет урок. Не верно, что сейчас идет урок).
Обозначения:
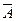 ,
,  А (приставка), not А
А (приставка), not А
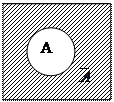 |
дополнение к множеству А
в теории множеств
Таблица истинности
| А | 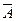
|
Реализация логического отрицания – инвертор.
|

|



4. Дополнительные логические операции:
1) Импликация (логическое следование) – это операция, которая выражается связками
а) если А, то В
б) из А следует В.
Обозначения:
А→В, А В ( импликация ложна, когда А-1, В-0 →0)
В ( импликация ложна, когда А-1, В-0 →0)
| А | В | А→В |
Пример:
Если идет дождь, то асфальт мокрый. (А – 0, А→В – 1)
 импликация зависит от основных операций
импликация зависит от основных операций
3) Двойная импликация или равносильность или эквиваленция– это объединение простых высказываний а и В в словосочетании с помощью < тогда и только тогда>.
Обозначения:
А↔В, А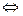 В, А=В, А~В.
В, А=В, А~В.
Таблица истинности
| А | В | А↔В |
Формула взаимосвязи с основными операциями:
|
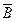 +А)
+А)