рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Философия
- /
- Курс лекций По дисциплине ДИСКРЕТНАЯ МАТЕМАТИКА
Реферат Курсовая Конспект
Курс лекций По дисциплине ДИСКРЕТНАЯ МАТЕМАТИКА
Курс лекций По дисциплине ДИСКРЕТНАЯ МАТЕМАТИКА - раздел Философия, Федеральное Государственное Бюджетное Образовательное У...
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
«МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ»
 ИНСТИТУТ ЭКОНОМИКИ, УПРАВЛЕНИЯ И ИНФОРМАЦИОННЫХ СИСТЕМ В СТРОИТЕЛЬСТВЕ
ИНСТИТУТ ЭКОНОМИКИ, УПРАВЛЕНИЯ И ИНФОРМАЦИОННЫХ СИСТЕМ В СТРОИТЕЛЬСТВЕ
(ИЭУИС)
Факультет информационных систем, технологий и автоматизации в строительстве
(ИСТАС)
Ф.К. Клашанов
Курс лекций
По дисциплине
ДИСКРЕТНАЯ МАТЕМАТИКА
Учебное пособие
Москва 2011
Клашанов Ф. К. Дискретная математика. Курс лекций. Учебное пособие. М.: МГСУ, 2011. – 198 с.
В учебном пособии по дискретной математике представлены материалы в помощь бакалаврам, изучающим дискретную математику в Московском государственном строительном университете на факультете ИСТАС и обучающихся по направлению подготовки 230100 «Информатика и вычислительная техника», а профиль подготовки: Автоматизированные системы обработки информации и управления в строительстве (АСОИУ) и Системы автоматизации проектирование (САПР) в строительстве. Учебное пособие представляет собой единый методически взаимоувязанный материал, состоит из следующих взаимосвязанных разделов: элементы теории множеств; сведения из булевой алгебры; элементы комбинаторики; основы теории графов. Учебное пособие взаимосвязано с методическими пособиями по практическим и самостоятельным работам, в которых даются математические понятия приведенные в учебном пособии. Материал рассчитан на односеместровое занятие на 108 часов, куда входят аудиторные и самостоятельные занятия. В конце каждой темы приведены вопросы для самоконтроля.
Учебное пособие будет полезно при изучении курса «Дискретная математика».
СОДЕРЖАНИЕ
| Лекция 1 …………………………………………………………………………………. ВВЕДЕНИЕ ……………………………………………………………………... Цель и задачи предмета ………………………………………………………. Предмет дискретной математики ……………………………………………. Основные разделы дискретной математики ………………………………. Изоморфизм …………………………………………………………………… Контрольные вопросы ………………………………………………………………… | |
| Лекция 2 …………………………………………………………………………………. ОСНОВЫ ТЕОРИИ МНОЖЕСТВ…………………………………………………... Интуитивное понятие множества. Основные принципы …………………. Множество и элементы множества …………………………………………. Конечные и бесконечные множества ……….………………………………. Задание множества .…………………………………………………………….. Мощность множества …………………………………………………………... Подмножество, собственное подмножество ……………………………….. Кортеж …………………………………………………………………………… Символический язык содержательных теорий множеств ……………… Добавление и удаление элементов …………………………………………. Булеан и универсумом ………………………………………………………. Диаграммы Венна (Круги Эйлера) …………………………………………… Ограниченные множества. Границы множеств ……………………………. Точная верхняя (нижняя) граница ………………………………………….. Принцип двойственности ……………………………………………………… Линейные пространства ………………………………………………………... Контрольные вопросы ………………………………………………………………… | |
| Лекция 3 …………………………………………………………………………………. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ……………………………………………... Симметрическая разность ……………………………………….……………. Дополнение ………………………….…………………………………………. Двуместные операции ……….…………………………………………………. Порядок выполнения операций .…………………………………………….. Теоретико-множественные тождества ……………………………………… Законы для объединения и пересечение …………………………..………. Законы для дополнений ………………………………………………………. Законы для разностей множеств …………….………………………………. Покрытие и разбиение множеств …..……………………………………… Частично упорядоченные множества …………………………………………….. Контрольные вопросы ………………………………………………………………… | |
| Лекция 4 …………………………………………………………………………………. ОТНОШЕНИЯ. ОТОБРАЖЕНИЯ. СООТВЕТСТВИЯ…………………………... Бинарные отношения …………………………………………….……………. Свойства бинарных отношений ………………………………………………. Отношение эквивалентности ……………………………………………. Отношениетолерантности .……………………………………………….. Отношения порядка ………………………………..……………………… Тернарные отношения ………………………………………………………… n-арные отношения …………………………..…………………………………. Отображения ……………………………………………………………………. Соответствие ……………………..………….…………………………………. Функция …..………………………………………………………..…………… Представление функции в терминах отношений ………………………….. Функции, функционалы, операторы ………………………………………….. Суперпозиция бинарных отношений ………………………………………. Обратная функция ………………………………………………………………. Классификация отображений ……………………………………………….. Операция ………………………………………………………………………… Частично упорядоченные множества ……………………………………….. Минимизации представления множества ………………………………….. Контрольные вопросы ………………………………………………………………… | |
| Лекция 5 …………………………………………………………………………………. ЭЛЕМЕНТЫ КОМБИНАТОРИКИ……….….……………………………………... Основные правила комбинаторики …………..………………………………. Правило произведения ……………………………………………………. Правило сумм ………………………………………………………………. Перечислительная комбинаторика ………………………………………….. Перестановки ………………………….…………………………………… Размещения ……………………………….………………………………… Размещения с повторениями …………….…………………….………. Упорядоченное размещение ……………………………………………. Сочетания ………………………….………………………………………. Сочетания с повторениями ……..………………………………………… Комбинации элементов с повторениями ……………………………… Бином Ньютона …………………………………………………………………. Разбиения. Комбинаторные числа Стирлинга и Белла …………………. Числа Стирлинга 2-го рода ……………………………………………... Метод производящий функций ………………………………………………... Контрольные вопросы ………………………………………………………………… | |
| Лекция 6 …………………………………………………………………………………. АЛГЕБРАИЧЕСКАЯ СИСТЕМА……….…………………………………………... Замыкание и подалгебры ………………………………………….……….… Морфизмы …..…………………….……………………………………………. Гомоморфизмы …………..…………………………………………………. Фундаментальные алгебры .……………….………………………………….. Алгебры с унарными операциями ……...…………………………………… Алгебры с бинарными операциями ………………………………………… Алгебры с одной бинарной операцией …………………………..…………. Полугруппа ………………………….……………………………………………. Моноид …………………………..…………….…………………………………. Группоид …..…………………………….……………………………………… Группа ……………………………………………………………………………… Абелева группа ………………………………………………………………… Алгебра с двумя операциями ……………………………………………….. Кольца ……………………….………………………………………………… Тело ……………………………………………………………………………. Поля …………………………………………………………………………… Отношения ……………………………………………………………………… Граф ……………………………………………………………………………… Матрица смежности ……………………………………………………………. Фактор-множества и фактор-алгебра …………………………………………… Целые числа по модулю m ………………………………………………………… Конгруэнции ………………………………………………………………………. Контрольные вопросы ………………………………………………………………… | |
| Лекция 7 …………………………………………………………………………………. ЭЛЕМЕНТЫ ТЕОРИИ ГРАФОВ…….……………………………………………... Определение ……………………………………….……………. ………………... Граф, вершина, ребро …………………………….………………………….……. Неориентированный граф ……….……………………………………………. Инцидентность, смешанный граф .…………………………………………….. Эквивалентный ориентированный граф ……………………………………… Обратное соответствие …………………….……………………………………… Изоморфизм графов ……………………………………..………………..………. Путь, ориентированный маршрут ………………………………………………. Смежные дуги, смежные вершины, степень вершины ………………………. Компонентная связность ………………...……………………………………… Граф со взвешенными дугами …………...……………………………………… Подграф …………...……………………………………………………………..… Контрольные вопросы ………………………………………………………………… | |
| Лекция 8 …………………………………………………………………………………. ДЕРЕВЬЯ…….…………………………………………………………………..……... Свободные деревья …………………………….……………. ………………... Ориентированные, упорядоченные и бинарные деревья …….………………….. Упорядоченные деревья ………………………………………………………. Представление деревьев в компьютере ………………………………………….. Контрольные вопросы ………………………………………………………………… | |
| Лекция 9 …………………………………………………………………………………. БУЛЕВА АЛГЕБРА...………………………………………………………………..... Основные логические функции ………………………………………………….. Булева функция ……………………………………………………….……………. Двухэлементная булева алгебра ……………………………………. ……………. Функции одной переменной y = f(x) ………………………………...................... Таблицы булевых функций ………………………………………………………. Функции двух переменных z = f(x,y) ……………………………………………… Порядок выполнения операций …………………………………………………… Эквивалентность формул …………………………………………………………. Графический способ задания булевой функции …………………………………. Фактор-алгебра алгебры формул ………………………………………………….. Контрольные вопросы ………………………………………………………………… | |
| Лекция 10 …………………………………………………………………………………. ДИЗЪЮНКТИВНЫЕ И КОНЪЮНКТИВНЫЕ НОРМАЛЬНЫЕ ФОРМЫ Определение ………………………….…………………………………………. Алгоритм приведения формулы к ДНФ ….……………………………………. Совершенные ДНФ (СДНФ) и КНФ (СКНФ) ……………………………….. Первая теорема Шеннона ……………….……………………………………… Вторая теорема Шеннона ………………………………………………………… Функциональная полнота ……………………………………………………..………. Алгоритм нахождения СДНФ ………………………………………………………. Минимизация булевых функций в классе ДНФ ….…………………………………. Метод Квайна …..……………………………………………………….. Контрольные вопросы ………………………………………………………………… | |
| Лекция 11 …………………………………………………………………………………. ПОЛНЫЕ СИСТЕМЫ БУЛЕВЫХ ФУНКЦИЙ ………………………………. Каноническое представление логических функций …………………………….. Системы булевых функций ….…………………………………………………. Теорема (о двух системах) ………..…………………………………………….. Базис Жегалкина ………………..……………………………………………… Классы булевых функций ………………………………………………………. Теорема (Пост-Яблонского) …………………………..…………………………. Теорема (Пост) ……………………………………………………………………. Алгебра Жегалкина …………………………….…………………………………. Контрольные вопросы ………………………………………………………………… | |
| Лекция 12 …………………………………………………………………………………. ЛОГИКА ВЫСКАЗЫВАНИЙ………………………………………………………. Определения ………………………….…………………………………………. Формулы логики высказываний………………………………………………. Порядок выполнения операций .…………………………………………….. Правила преобразования формул ……………………………………… Основные равносильности ……………..……………………………………… Правило перехода к булевым функциям …………………………..………. Нормальные формы формул логики высказываний ………………………. Законы логики высказываний. Тавтологии .…………………………………. Контрольные вопросы ………………………………………………………………… | |
| Лекция 13 …………………………………………………………………………………. ЛОГИКА ПРЕДИКАТОВ………………………………………………………. Определение предиката …………………………………………………………. Язык логики предикатов……….…………………………………………………. Логические операции (связки) над предикатами………………………….…….. Кванторы ………………………………………………….………………………… Квантификация многоместных высказывательных форм ……………………… Булева алгебра предикатов …………………………………..…………..………. Формулы ……………………..…………………………………………………. Алгоритм преобразования формул в нормальную форму……………………. Исчисление предикатов …..……………………………………………………… Следование и эквиваленция ……………………………………………………… Правила вывода исчисления предикатов ……………………………………….. Отрицания в исчислении предикатов ……………………………………………. Контрольные вопросы ………………………………………………………………… |
Лекция № 1
В России исторически сложилось так, что представление об образовании включает в себя органичное единство школы как системы приобретения знаний, фундаментальной науки как показателя уровня подготовки специалистов и гуманитарной культуры как основы духовного богатства человека.
Садовничий В.А. академик РАН,
из предисловия С.В. Яблонский Введение в дискретную математику. М.: Высшая школа, 2003
ВВЕДЕНИЕ(2 часа)
Цель и задачи предмета
Данное учебное пособие представляет собой единый методически взаимоувязанный материал, который будет полезен студентам, изучающим дискретную математику в Московском государственном строительном университете на факультете ИСТАС и рассчитан на студентов, обучающихся по специальности 220200 «Автоматизированные системы обработки информации и управления» (код по ОКСО 230102) по направлению 654600 «Информатика и вычислительная техника» (код по ОКСО 230100), а также по специальности 220100 – Вычислительные машины, комплексы, сети системы. Тематикой данного пособия являются языки, модели и методы решения задач теории множеств, математической логики и теории графов, интерпретированные на дискретные объекты.
Исследование, особенно с количественной оценкой, предусматривает разработку адекватных информационных систем, включающих в себя моделирование, анализ и синтез. Скоростная и качественная технология обработки информации отображающей реальный мир во всех его проявлениях не мыслима без компьютеров, как персональных так и суперЭВМ. Для этого необходимо построить модель реальных объектов и процессов их преобразования в виде дискретных конструкций, поскольку именно цифровые ЭВМ получили наиболее сильное развитие. Благодаря потребностям компьютерных технологий динамично стала развиваться дискретная математика.
Как отмечает /60/, в истории развития цивилизации человечества можно выделить три периода: аграрный, индустриальный и информационный. Аграрный период, закончившийся в XVII, являлся основоположником элементарной математики (арифметики) количественно описывающей материальное представление мира и удовлетворявшейся числом. Индустриальный период, с XVII по XX века, потребовал развития другого уровня математики, описывающей процессы и их развитие, как в пространстве, так и во времени и потребовал развития высшей математики – анализа, введения функции. Информационный период начался с XX века, базируется на обработке информации, и потребовал развития дискретной математики, основанной на алгебре и использующей понятия радикала.
Таким образом, математику как науку можно разделить на дискретную и непрерывную (континуальную). В континуальной математике явно или неявно содержится идея теории пределов и непрерывности, применявшаяся при решении задач сплошных сред. С развитием физики стал развиваться квантовый подход к описанию вещества. Все остальное, что не относится к континуальной математике – это дискретная математика, куда в частности входят арифметика, алгебра, теория множеств и общая теория отображений, математическая логика, комбинаторный анализ, теория алгоритмов и др. Дискретная математика особенно активно стала развиваться в XX веке, как основная ветвь математики. Это объясняется следующими причинами:
· язык дискретной математики является метаязыком всей современной математики;
· дискретная математика – это теоретическая основа компьютерной математики;
· модели и методы дискретной математики являются хорошим средством и языком для построения и анализа моделей в различных науках, включая и вопросы, связанные со строительством;
· проблемы абстрагирования конкретной проблемы и перевода ее на язык доступный ЭВМ наиболее просто и объемно решаются методами дискретной математики.
Цель читаемого курса – помочь студентам овладеть математическим аппаратом синтеза и анализа дискретных структур (систем с сосредоточенными параметрами; процессов, протекающих в дискретные моменты времени), а его содержанием - являются теория множеств, математическая логика и теория графов. Студент должен самостоятельно изучить соответствующий теоретический материал и ознакомиться с решением типовых примеров, приведенных в настоящем учебнике. Задачи по дискретной математике не требуют предварительных дополнительных знаний и любой здравомыслящий человек, претендующий на получение высшего технического образования, должен суметь выполнить эти задачи. Важность изучения дискретной математики проявляется в том, что, современная жизнь абсолютно немыслима без компьютеров, а в основе любого вычислительного устройства лежат знания именно дискретной математики, (которая является наукой 21-го века, и без ее развития немыслимы успехи технического прогресса). Поэтому освоение элементарных знаний в области дискретной математики расширит кругозор студента, повысит его математическую культуру и позволит ему в какой-то степени понимать работу вычислительных устройств и лучше ориентироваться в современном мире. Дискретная математика является основой для таких спецкурсов, как базы данных и базы знаний, теории алгоритмов, компьютерной алгебры, геометрии, текстовых и графических редакторов и т.п. В классический курс дискретной математики входят также такие разделы, как кодирование (необходимое для безошибочной передачи информации на расстояние, именно с помощью кодирования работают Интернет и электронная почта), теория графов и алгоритмов. Тема теории графов важна тем, что она помогает проанализировать ряд прикладных задач в том числе и сети (сетевой граф).
В течение учебного года по дискретной математике будет рассматриваться следующая тематика: основы теории множества, алгебра высказываний, алгебра предикатов, булевы функции, элементы теории и практики кодирования, теория графов, элементы теории конечных автоматов, машина Тьюринга и соответственно учебное пособие курса лекций состоит из взаимосвязанных разделов, раскрывающих вышеуказанную тематику. В конце каждой раздела приведены задачи и упражнения, которые целесообразно разобрать на практических и лабораторных занятиях.
Пособие будет полезно так же для программистов, желающих расширить область своих знаний в области применения дискретной математики применительно к строительству, а также пополнить свои практические навыки теоретическими знаниями.
Предмет дискретной математики
В курсе математического анализа изучаются функции, определённые на числовой прямой или на отрезке числовой прямой или на (гипер-) плоскости и т.п.… Простейшим (но нетривиальным) таким множеством является множество, состоящее… Такие понятия как «множество», «событие», которые часто используются в бытовой лексике, не имеют точного определения в…Основные разделы дискретной математики
Логика возникла тогда, когда человечество сделало актуальным вопрос, как надо рассуждать, чтобы получить правильные выводы. Активный интерес к логике среди математиков и философов приходится на период расцвета греческой культуры в VI-IV вв. до н.э. Первое большое сочинение, посвященное специально логике – это "Аналитики " Аристотеля, (384 - 322 гг. до н.э. ). Параллельно и независимо возникла буддистская логика. В Европе развитие логики начинается от изучения Аристотеля. В "обычную" логику начинают проникать математические и логические знаки с целью замены слов обычного живого языка. Появилась идея о том, что, записав все исходные допущения на языке специальных знаков, похожих на математические, можно заменять рассуждения вычислением. В последствии правила логических вычислений были переведены на язык вычислительной машины, которая выдает следствия из введенных в нее исходных допущений. Такую "логическую машину" сконструировал еще в средние века Раймунд Луллий (1235-1315). Далее Лейбниц (1646-1716) внес свой вклад в универсальное логическое исчисление в надежде, что в будущем философы вместо того, чтобы бесплодно спорить, будут брать бумагу и вычислять, кто из них прав.
Начало созданию аппарата современной математической логики (логики высказываний) заложил Джордж Буль (1815-1864). Логико-математические языки и теория их смысла были затем значительно развиты в работах Фрече (1848-1925). Применение математической логики в некоторых разделах математики произвел Пеано (1858-1932). В 20-м веке – это работы Рассела и Уайтхеда, изданные в 1910 - 1913 гг. и программа обоснования математики на базе математической логики, предложенная крупнейшим математиком Гильбертом (1862-1943). В принципе с программы Гильберта и начинается современное развитие математической логики. В этот период происходит применением точных математических методов при изучении формальных аксиоматических теорий /7/. Символический язык математической логики оказался очень важным подспорьем в изучении логических основ математики, поскольку он позволял избегать всякой неточности мысли, которая может иметь место при использовании слов обычного языка. Смысл слов живого языка даётся не точным определением, а созданием привычки к принятому словоупотреблению.
Особенно широкий интерес к математической логике стал проявляться не только среди математиков, но и среди техников, когда обнаружилось, что в рамках математической логики уже создан аппарат для расчёта действия самых различных вычислительных и управляющих дискретных устройств.
В математической логике предметом исследования оказываются математический анализ, алгебра, элементарная геометрия, арифметика и др. В логике математические теории изучаются в целом - и это одна из особенностей математической логики по сравнению с другими математическими дисциплинами. Математическую теорию описывают на базе логико-математического языка, этот этап называется формализацией теории. После формализации полученную формальную аксиоматическую теорию подвергают точному математическому изучению с точной постановкой проблемы и получением математических результатов. Такими проблемами могут быть: непротиворечивость теории, т.е. не выводится ли в данной теории некоторое утверждение и его отрицание. Так, с помощью метода интерпретаций Кэли и Клейн показали, что геометрия Лобачевского непротиворечива, если непротиворечива, обычная евклидова геометрия. К настоящему времени непротиворечивость таких теорий, как элементарная геометрия, арифметика, анализ, хорошо изучена и достаточно надёжно обоснована.
Следующая проблема – это полнота теории. Во многих математических теориях возникают конкретные проблемы, которые не удаётся ни доказать, ни опровергнуть. Иногда это бывает в силу технической сложности самой проблемы, но спустя определённое время, проблему всё же удаётся разрешить. Но возможна и такая ситуация: проблему невозможно ни доказать, ни опровергнуть в рамках исследуемой теории. Математик Гедель доказал теорему о неполноте, которая утверждает, что всякая достаточно богатая теория необходимо содержит утверждения, которые нельзя ни доказать, ни опровергнуть в рамках теории. Но такие теории, как элементарная геометрия, теория векторных пространств оказываются полными. Татарский в 1948 г. построил конкретный алгоритм, позволяющий по всякому утверждению элементарной геометрии выяснить, является ли это утверждение истинным или ложным.
Методами логика можно доказать, что многие теории, например арифметика, анализ, теория множеств, неразрешимы, т.е. не существует алгоритма, позволяющего по всякому суждению теории узнавать, истинно оно или ложно. Вопрос о существовании тех или иных алгоритмов занимает важное место в исследованиях логикой. Большое внимание уделяется изучению сложности алгоритмов. Так, например, недавно было показано, что арифметика (сложение натуральных чисел), являющаяся разрешимой теорией, может иметь только очень сложные разрешающие алгоритмы.
Вопросы построения оптимальных по сложности и по времени работы вычислительных устройств занимают важное место в теоретической кибернетике - науке, тесно связанной с математической логикой.
Если коснуться истории, то математический аппарат, пригодный для описания систем событий, возник первоначально в качестве аппарата символической логики /7/. Создание «алгебры высказываний» связано с именем Дж. Буля (1815— 1864), хотя и у него были предшественники, к которым в первую очередь относятся Лейбниц и братья Бернулли. Появившаяся в 1847 г. работа Буля положила начало исследованиям, результатом которых был расцвет математической логики, составляющий одну из характернейших черт математики двадцатого века. В своей монографии «Исследование законов мышления, на которых основаны математические теории логики и вероятностей» отчетливо указал на связь построенного им исчисления так же с основаниями теории вероятностей. Эта связь основывается на аналогии между «событиями» и «высказываниями», позволяющей обслуживать логику и теорию вероятностей одним формальным аппаратом. Так как «событие» — это то, что может произойти или не произойти; «высказывание» же — это то, что может быть истинно или ложно. Среди событий есть достоверные и невозможные; высказывания могут оказаться тождественно истинными или тождественно ложными. Между событиями возможна причинно-следственная связь: одно событие бывает иногда следствием другого. Точно так же между высказываниями возможна логическая связь; они могут вытекать одно из другого. Каждому событию может быть сопоставлено некоторое высказывание, утверждающее, что это событие произошло. С другой стороны, всегда можно истолковать высказывание как утверждение об осуществлении некоторого события. Сказанное сейчас убеждает в возможности построения единого «исчисления», которое могло бы, смотря по обстоятельствам, служить то «исчислением высказываний», то «исчислением событий». Такое исчисление и было создано Дж. Булем.
В течение полувека оно развивалось в чисто «логическом» русле. Мерное значительное исследование по аксиоматике теории вероятностей появилось лишь в 1917 г.; его автором был С. Н. Бернштейн. Последующие исследования в этой области, связанные в первую очередь с работами А. Н. Колмогорова, окончательно поставили теорию вероятностей на твердую почву и оказали большое влияние на смежные разделы математики, в особенности - на теорию меры.
В 20 и 21 веках в связи с развитием компьютерных технологий алгебраические методы все более активно применяются во всех областях человеческой деятельности, в том числе и технологии строительства и производства строительных машин и материалов. Но применение вычислительной техники в различных сферах человеческой деятельности базируются на вычисления на дискретных структурах. Разработка комплексных интегрированных автоматизированных систем обработки информации и их компонент требует знаний дискретной математики, в которой отсутствует предельный переход и непрерывность, что уже знакомо студенту при изучении классического анализа.
Дискретная математика является одним из основных для дальнейшего изучения и практического решения задач, встречающихся при производстве строительства. Логика применения дискретной математики в данном случае сводится к следующему. Требуется четко и лаконично описать реальную ситуацию, имеющую место при производстве строительства, на обычном языке. Затем сделать перевод понятий обычного языка на язык символики дискретной математики. Для анализа задач строительства нужно после получения решения алгебраической задачи провести обратный перевод – с алгебраического на технический язык.
Для производства решения разрабатываются алгоритмы, учитывающие аппаратурные возможности (емкость памяти) и временной фактор при условии, что сходимость и устойчивость задачи обеспечена. Емкостные и временные проблемы связаны с размерностью задачи и выбором эффективного алгоритма. Решение таких задач возможно на основе теории алгоритмов. Вычисления на ЭВМ производятся на дискретных структурах, где необходима комбинаторная грамотность. Таким образом, сама жизнь требует изучения дискретной математики.
Дискретная математика является одним из разделов математики. Любая математическая теория имеет дело с двумя объектами /5/ с множествами и функциями (соответствиями, отношениями) на этих множествах. Если аргументы функции f пробегают множество M и функция принимает значения, принадлежащие этому же множеству f, то эта функция f называется алгебраической операцией на множестве M. Вот это и есть первые примеры введения абстрактных символов для решения реальных практических задач.
Элементы булевых алгебр будут использоваться при изучении теории вероятностей, функционального анализа, теории меры. Булева алгебра—это алгебраическая система, которая в зависимости от обстоятельств может быть интерпретирована либо как система событий, либо как система высказываний (допуская и иные истолкования). Аксиомы булевой алгебры выражают то общее, что роднит «события» и «высказывания». Причинно-следственная связь событий или логическая связь высказываний описывается формулами, имеющими вид неравенств. Булева алгебра представляет собой разновидность частично упорядоченного множества: неравенство х<у выражает «большую достоверность» события у по сравнению с событием х или «большее правдоподобие» высказывания усравнительно с х. Среди элементов булевой алгебры должны содержаться наибольший и наименьший, соответствующие «абсолютно достоверному» и «абсолютно невозможному» событиям («тождественно истинному» и «тождественно ложному» высказываниям). Каждый элемент должен иметь дополнение, которое можно истолковывать как «событие, противоположное данному» или как «отрицание данного высказывания».
Эти проблемы весьма разнообразны, они соприкасаются с логикой и теорией множеств, с теорией вероятностей и анализом. Такое обилие точек соприкосновения со смежными математическими дисциплинами роднит теорию булевых алгебр с функциональным анализом, к которому она близка и по своему общему математическому стилю.
Элементы комбинаторики широко используются при изучении теории вероятностей. В этом разделе приводятся основные определения и обозначения, относящиеся к используемым логическим и теоретико-множественным понятиям, а также представленные в приводимых ниже алгоритмах. Начинается все с логических и теоретико-множественных понятий.
Теория графов /2/ может быть использована при решении задач исследования операций, вычислительной математики, теории управления.
Изучив свойства достижимости и связности графов, вопросы построения сильных компонент и баз можно в качестве практической задачи рассмотреть вопросы образования группировок правления и коалиций в организациях .
Теория графов позволяет оптимально составлять расписания, например, работы транспорта, задачу оптимального размещения ресурсов, доставки, размещения на сети дорог всевозможных служб, таких, как пожарные команды, милицейские участки, станции скорой помощи, размещение складов или переключательные пункты в системах доставки товаров или в сетях связи и т.п.
Задачи о деревьях, кратчайших остовах и задача Штейнера позволяют применить их для практических задач: к проектированию электрических и газовых распределительных сетей.
Задача поиска кратчайшей цепи между парами вершин и ее приложения к задачам выбора маршрута для максимизации пропускной способности или надежности, к специальному случаю сетей и к анализу критических маршрутов и кратчайших цепей.
Задачи поиска циклов в графах, общие циклы и разрезы. Здесь же разбираются задача поиска эйлеровых циклов и задача китайского почтальона с ее приложениями к сборке мусора, к доставке молока или почты и к инспектированию систем с распределенными параметрами.
Рассматривается задача нахождения гамильтонова цикла в неполном графе и ее приложение к машинному планированию, задаче поиска кратчайшего гамильтонова цикла, широко известного под названием «задача коммивояжера», и ее приложениям к выбору транспортных маршрутов.
Исследуются максимальные потоки и минимальные стоимости — задачи о максимальных потоках в графах, дугам которых приписаны пропускные способности и стоимости. Задачи о потоках в графах, у которых дугам приписаны выигрыши, встречаются при рассмотрении математических моделей арбитража, активных электрических цепей и т. д. Задачи о таких потоках также обсуждаются здесь.
Вычисление максимальных паросочетаний графов и описывается обобщенный венгерский алгоритм. Подробно алгоритм разобран для двудольных графов, для случаев транспортной задачи и задачи о назначении, играющих большую роль в исследовании операций с приложениями к назначению людей на работу, размещению вспомогательных служб, составлению маршрутов транспортных средств и т. д..
Изоморфизм
Отображение µ множества X на множество Y является изоморфизмом (изоморфным отображением), если оно взаимно однозначно и сохраняет порядок, то есть… Обратное отображение также является изоморфизмом. Такие отображения, то есть… Взаимно однозначное отображение ω множества X на множество Y называется дуальным изоморфизмом, если x ≤ y…Упражнения
2. Запишите на языке множеств свою группу. 3. Запишите на языке множеств предметы, которые изучаете. 4. Выделите элемент в группе, изучаемых предметов.ОСНОВЫ ТЕОРИИ МНОЖЕСТВ
Понятие множества — одно из основных, если не основное, понятий математики. Оно не имеет точного определения, и его следует отнести к аксиоматическим понятиям. Такими аксиоматическими понятиями, например, в элементарной геометрии являются понятия точка, прямая, плоскость.
Как правило, термин множество объясняется с помощью примеров, а потом указываются правила его использования в математических применениях. Последнее можно сделать на разных уровнях строгости. Детальное и строгое изложение теории множеств требовало бы скрупулезного анализа логики математических суждений, а это — специальная самостоятельная тема, которая относится к области основ математики. Для наших целей достаточно выбрать уровень так называемой интуитивной теории множеств.
Интуитивное понятие множества. Основные принципы
Как было сказано выше, понятие множества относится к аксиоматическим понятиям математики, и точное его определение дать невозможно. Часто принимается формулировка интуитивного понятия множества Г. Кантора, основоположника этой теории:
"Произвольная совокупность определенных предметов нашей интуиции или интеллекта, которые можно отличить один от другого и которые представляются как единое целое, называется множеством. Предметы, которые входят в состав множества, называются его элементами".
Множество и элементы множества
Агрегатная точка зрения рассматривает множество как набор вещей (по Кантору), а с атрибутивной точки зрения множеством считается свойство (атрибут)… Символическая запись этих точек зрения следующая: (m есть элемент множества М).Конечные и бесконечные множества
Как видно из приведенных примеров число элементов, образующих множество, может быть конечно или бесконечно. В первом случае множество называется… Множество, не содержащее элементов, называется пустым. Принято его обозначать… Если элемент т принадлежит множеству М, то используется запись включение ,которое указывает, что т является элементом…Примеры
Множество степеней 2, заключенных между 1 и 10 – {1, 2, 4, 8}
Множество адресуемых ячеек памяти компьютера.
Множество программ исполнимых компьютером.
Множество тактов работы процессора.
В компьютере все множества реальных объектов конечны.
Задание множества
Чтобы задать множество, нужно указать, какие элементы ему принадлежат. Если для данного элемента условие выполнено, то он принадлежит определяемому множеству, в противном случае - не принадлежит.
Множество может быть задано различными способами:
Перечисление элементов. Перечисление элементов применимо только для конечного множества. Для задания множеств используются фигурные скобки { }, в которые записывают обозначения элементов множества и разделяют их запятой.
Характеристический предикат. Множество задается указанием свойств элементов Р(х), которые записываются в фигурных скобках { }, т.е при помощи характеристического предиката: М : = {m| Р(х)}. Характеристический предикат — это некоторое условие, выраженное в форме логического утверждения или процедуры, возвращающей логическое значение, и позволяющее проверить, принадлежит ли любой данный элемент множеству. Вообще предикат – это высказывание, содержащее одно или несколько переменных, т.е повествовательное предложение, которое может быть только истинным или ложным.
Порождающая процедура. При задании множества порождающей процедурой множество имеет вид: М: = {х | х: =f}. Порождающая процедура - это процедура, которая в процессе работы порождает некоторые объекты, являющиеся элементами определяемого множества.
Пример.
А. Множество М цифр десятичного алфавита можно задать в виде М = {0, 1,...,9} - перечисление элементов.
Б.М = {i|i - целое, 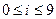 }, где справа от наклонной черты указано свойство элементов этого множества – характеристический предикат.
}, где справа от наклонной черты указано свойство элементов этого множества – характеристический предикат.
Множество М четных чисел можно записать в виде М = {т/т - четное число} . характеристический предикат.
В. М := {i|i := 0; for i from 0 to 9 do i := i + 1; yield i end for}, - множество задано порождающей процедурой.
Перечислением можно задавать только конечные множества. Бесконечные множества задаются характеристическим предикатом или порождающей процедурой.
Мощность множества
Множества, эквивалентные множеству всех действительных чисел, принадлежащих интервалу [0,1] имеютмощность континуума. Название «континуум»… Мощность объединения множеств. Число элементов (мощность) конечного… |АB| = |А| + |B| - |АB|,А1A2A3| + … + |А1A2A3| + … + |А1A2An| + … + |Аn-2An-1An| + (-1)n-1 |А1A2A3…An|.
. Если множество А конечно, |А| = k, то элементы А всегда можно перенумеровать,… По определению .Подмножество, собственное подмножество
Множество М', каждый элемент, которого является элементом другого множества М, называется подмножеством данного множества М. Таким образом,… , где - знак включения подмножества; — «если..., то....», — «если и только если...».Кортеж
Определение. Пусть даны множестваХ1 ,Х2, ...,Хnкортежемдлинып,составленным из элементов этих множеств, называется конечнаяпоследовательностьα = { х1 ,х2, ...,хn },где для всехk, 1 ≤ k ≤ п,имеемхk  Хk
Хk
Элемент хkназывается k-й координатой или k -й компонентой кортежа α.
Два кортежа равны в том и только в том случае, когда они имеют одинаковую длину, причем их координаты, стоящие на местах с одинаковыми номерами, равны, т.е. кортежи α = { х1 ,х2, ...,хm } и β = { y1 ,y2, ...,yn } равны только в том случае, когда т = п, причем хk = уk для всех 1 < k < п.
Кортежи длины два называют упорядоченными парами, длины три — упорядоченными тройками, длины n — упорядоченными n-ками. Для краткости речи слово «упорядоченные» часто опускают.
Кортеж, не содержащий ни одной координаты, т.е. кортеж длины 0, называется пустым.
Основные отличия понятий кортежа и множества следующие:
а) в множестве порядок элементов не играет роли, а кортежи, отличающиеся порядком элементов, различны, даже в случае, когда они имеют одинаковый состав;
б) в множестве все элементы различны, а в кортеже координаты могут повторяться.
В дальнейшем, чтобы различать множества и кортежи, будем элементы множества заключать в фигурные скобки, а координаты кортежа — в угловые.
Пусть А1, А2, ..., Ап — некоторые множества. Их декартовым произведением называют множество, состоящее из кортежей вида <а1, а2,..., an>, где а1  A1, а2
A1, а2  A2,; а3
A2,; а3  A3,; ...; аn
A3,; ...; аn  An,. Декартово произведение обозначается так:А1 × А2 × ... × Ап.
An,. Декартово произведение обозначается так:А1 × А2 × ... × Ап.
Произведение А × А × ... × А ( п раз) сокращенно обозначается как Аn и называется декартовой n-й степенью множества А.
Таким образом, подводя итог выше сказанному, можем дать следующее определение.
Конечная последовательность, допускающая повторения элементов данного множества (или данных множеств), называется кортежом (n-кой, вектором, набором, упорядоченным множеством).
Условно кортеж записывают в угловых скобках ‹a,b,c›
Примеры:
1. Слово в алфавите A есть кортеж.
2. Команда в программе для ЭВМ есть последовательность символов из алфавита языка программирования.
3. Алфавит русского языка есть алфавит.
4. Программа для ЭВМ есть кортеж команд.
5. Координаты точки в n-мерном пространстве образуют кортеж.
Отметим следующее:
1. В условной записи кортежа элементы, его образующие, называются компонентами (координатами).
2. Число компонент кортежа называется его длиной. Так принято кортеж длиной два ‹a1,a2› называть парой (или упорядоченной парой), кортеж длины три ‹x1,x2,x3› - тройкой. В общем случае ‹a1,a2› ≠ ‹a2,a1›.
3. Кортеж длины n можно интерпретировать как n-мерный вектор, или как точку в n-мерном пространстве, а каждую компоненты кортежа можно рассматривать в этом случае как проекцию вектора на соответствующую ось.
Символический язык содержательных теорий множеств
Под языком теории множеств будем понимать реляционную систему, основным множеством которой являются символы алфавита A, а отношения позволяют… В этом плане L = ‹A,B›, BAA2 ... An, FB. Логическая экспликация понятия подмножества А мн-ва М с агрегатной и атрибутивной точек зрения следующая:Доказательство
then х' else х end if . Другими словами, на элементах из В мы пользуемся заданным соответствием, а… СЛЕДСТВИЕ Все подмножества конечного множества конечныДобавление и удаление элементов
. Аналогично, если А — множество, а x - элемент, причем , то элемент х можно… .Булеан и универсумом
Для каждого множества М существует множество, элементами которого являются подмножества множества М и только они. Такое множество будем называть семейством множества М или булеаном этого множества и обозначать В(М), а множество М — универсальным, универсумом или пространством и обозначать 1.
Пример.
Образовать булеан В(1) от универсума 1 = {у, х, а}.
Решение. Первым множеством является пустое множество  , не содержащее ни одного элемента. Затем образуем множества, содержащие по одному элементу – их будет равно числу сочетаний
, не содержащее ни одного элемента. Затем образуем множества, содержащие по одному элементу – их будет равно числу сочетаний  , затем множества, содержащих по два элемента, которых будет
, затем множества, содержащих по два элемента, которых будет  , и, наконец, множество, содержащее все элементы множества 1. В рассматриваемом случае
, и, наконец, множество, содержащее все элементы множества 1. В рассматриваемом случае
В(1)= { ,{у}, {х}, {а}, {у,х}, {а,х}, {а, у}, {у, х, а}}.
,{у}, {х}, {а}, {у,х}, {а,х}, {а, у}, {у, х, а}}.
Мощность |В(М) булеана от универсумома М равна 2|M|, т.е. В(М) = 2М.
Диаграммы Венна (Круги Эйлера) Джон Венн (1834-1923) Леонард Эйлер (1707-1783)
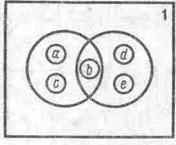 Множество также часто задают графически с помощью диаграмм Эйлера.
Множество также часто задают графически с помощью диаграмм Эйлера.
Например, задание множества {{а, b, с}, {b, d, е}} в пространстве 1 = {а, b, с, d, е} приведено на рис. 1.1, где замкнутая линия, называемая кругом Эйлера, соответствует одному из рассматриваемых множеств и ограничивает его элементы, при этом рамка, в верхнем правом углу которой стоит1, ограничивает элементы пространства. Другие способы задания множеств будут рассмотрены по мере необходимости.
На рис. 1.1 приведены диаграммы Венна, (называемые также иногда кругами Эйлера), иллюстрирующие операции над множествами. Сами исходные множества изображаются фигурами (в данном случае овалами), а результат графически выделяется (в данном случае для выделения использована штриховка).
Ограниченные множества. Границы множеств
Верхней гранью (границей) функции f(х) называется такое число С, что для любого элемента xX С≥f(х). Нижней гранью (границей) функции f(х)называется такое число d, что для любого… Границы С, d оценивают значение функции f(х) сверху и снизу.Точная верхняя (нижняя) граница
Утверждение. Пересечения {} не могут содержать более одного элемента Доказательство. Пусть. Тогда х ≤ у, поскольку. Аналогичным образом убеждаемся в справедливости противоположного неравенства y…Если х1 ≤ у1,х2 ≤ у2, ....хn ≤ уn, то


Принцип двойственности
Пусть К - некоторой класс частично упорядоченных множеств, содержащий вместе с каждым входящим в него частично упорядоченным множеством X также некоторое ему дуально изоморфное. На основании упомянутых свойств 7, 8
7. Если φ- дуальный изоморфизм, то всегда
 ,
, 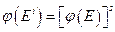 .
.
8. Если φ- дуальный изоморфизм то всегда
, .
можно утверждать, что всякое утверждение, относящееся к свойствам порядка и справедливое для любого 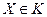 , перейдет после замены содержащихся в его формулировке неравенств противоположными, верхних границ нижними, а нижних — верхними в утверждение, также справедливое для всех
, перейдет после замены содержащихся в его формулировке неравенств противоположными, верхних границ нижними, а нижних — верхними в утверждение, также справедливое для всех 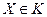 .
.
Сформулированный принцип называется общим принципом двойственности для частично упорядоченных множеств.
Точная верхняя (нижняя) граница множества
Утверждение.
Верхняя (нижняя) грань, если она существует, обязательно единственна.
Доказательство.
Пусть  . Тогда x ≤ y, поскольку
. Тогда x ≤ y, поскольку  ,
, 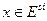 . Аналогичным образом убеждаемся в справедливости противоположного неравенства y ≤ x, а это означает, что x = y. Ч.т.д.
. Аналогичным образом убеждаемся в справедливости противоположного неравенства y ≤ x, а это означает, что x = y. Ч.т.д.
Точная верхняя граница (supremum) множества E обозначается символом sup E, точная нижняя граница (infimum) - inf E.
Основные свойства верхних и нижних границ
1. Если , то , 2. Если и существуют sup E1 и sup E2 (inf E1 и inf E2), тоМножество с атрибутивной точки зрения
В рамках атрибутивной точки зрения множества отождествляются со свойством, определяющим соответствующую совокупность элементов. В этом случае… Любому св-ву мн-ва М соответствует потенциально бесконечная совокупность… Пример:Структура
Лемма 1. В любой структуре всякое конечное множество элементов имеет точные границы. Упражнения 1.Упростить выражениеКонтрольные вопросы и задачи
1. Дайте определение множества.
2. Что такое множество? Как его обозначить? Как можно задать множество? Что такое подмножество?
3. Когда множество считается заданным?
4. Как принято обозначать и задавать множества? Приведите примеры задания множеств.
5. Какое множество называется пустым?
6. Когда множества равны?
7. Равны ли множества А = {а,b, с, d}, В = {а, b, с, d}?
8. Что такое семейство множеств?
9. Из скольких множеств состоит семейство А = {{0}, {1,2}, {1,2},{0}}?
10. Принадлежит ли элемент 2 множеству A={{ 1,2}, {1,2, 3}}?
11. Дайте определение включения множеств.
12. Является ли множество A = {х |0 ≤ х ≤ 1} подмножеством В = {х| 1≤ х≤ 3}, подмножеством С = {х |-3 ≤.х ≤2}?
13. Какое минимальное число подмножеств имеет не пустое множство?
14. Запишите все подмножества множества А = {1, 4}.
15. Перечислите все элементы индексированного множества Z = {zi|1≤i≤3}. Запишите индексное множество.
16. Какие множества называются конечными? Приведите примеры конечных и бесконечных множеств.
17. Выпишите элементы объединения множеств А = {а,b}, В = {1,b}, С = {1,d}.
18. Выпишите элементы пересечения множеств A = {{a,b}, { }, {a}}, B={{с},{a},{1}}.
}, {a}}, B={{с},{a},{1}}.
19. Выпишите элементы множества М = А - В для множеств' .4 ={1,3, 5}, В ={5, 6, 7}.
20. Выпишите элементы множества М = (А - В) (А
(А В) для множств А = {1, 2, 3, 4, 5}, В = {3, 4, 5}; для множеств А = {2, 4, 5}, B = {1, 4}; для множеств А = {1}, В =
В) для множств А = {1, 2, 3, 4, 5}, В = {3, 4, 5}; для множеств А = {2, 4, 5}, B = {1, 4}; для множеств А = {1}, В =  .
.
21. Дайте определение разбиения множества. Приведите все разбиения для множества А = {a, b, с}.
22. Какие множества называются эквивалентными? В каких случаях эквивалентны конечные и бесконечные множества?
23. Дайте определение счетного множества.
24. Что такое мощность множества? Дать определение.
25. Чему в математике служат отношения?
26. Как классифицируются отношения в зависимости от числа связей между элементами множества?
27. Дайте определение бинарного отношения.
28. Что представляет собой декартово произведение множеств?
29. Выпишите декартовы произведения множеств А = {а, b}, В = {1, 3}; декартового квадрата А = {1, а}.
30. Сколько элементов включает декартовый квадрат множества A = {1, 2,...,i, ...,n}?
31. Дайте определение бинарного, тернарного и n-арного отношения в терминах множеств.
32. Что понимают под рефлексивными и антирефлексивными отношениями?
33. Как характеризуются симметричные, асимметричные и антисимметричные отношения?
34. Дайте определение транзитивного отношения.
35. Дайте определение отношения эквивалентности и приведите примеры.
36. Какое отношение называется отношением нестрогого порядка? Является ли отношение ≤ на множестве А = {1, 2, 3} отношением нестрогого порядка?
37. Какое отношение называется отношением строгого порядка?
38. Какое множество называется упорядоченным, полностью упорядоченным?
39. Что такое линейный порядок?
40. Дайте определение функции.
41. Является ли отношение R = {<1,а>, <1,b>, <2,а>}, определенное на декартовом произведении множеств А = {1,2}, B = {а, b}, функцией?
42. Является ли функция f(х) = х2 инъективной?
43. Что представляет собой функционал?
44. Как в математике определяется пространство?
45. Какое пространство называется метрическим?
46. Что представляет собой линейное пространство?
47. Дайте определение линейного нормированного пространства.
7.
Контрольные вопросы
1. Какие основные символы, используемые в теории множеств, вы знаете?
3. Какие основные операции выполняются над множествами?
4. Какое множество можно назвать универсальным?
5. Что такое диаграмма Эйлера-Венна? Проиллюстрируйте с помощью диаграммы Эйлера-Венна объединение и пересечение трех множеств.
6. Каковы соотношения между множествами и составными высказываниями?
7. Сформулируйте и докажите основные тождества алгебры множеств.
8. Что называется кортежем и какие кортежи называются равными?
9. Что такое: декартово произведение множеств; декартова степень некоторого множества А; бинарное отношение, заданное на множестве А?
10. Назовите основные свойства бинарных отношений. Какое отношение называется рефлексивным, симметричным, антисимметричным, транзитивным? Какое отношение называется отношением эквивалентности?
11. Дайте определение отображения множества А во множество В. Поясните термин «мощность множества».
12. Что такое сюръекция, инъекция, биекция?
Лекция № 3
Подобно тому, как дар слова обогащает нас мнениями других, так язык математических знаков служит средством еще более совершенным, более точным и ясным.
Н. И. Лобачевский
ОПЕРАЦИИ НАД МНОЖЕСТВАМИ
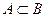 означает, что
означает, что 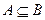 и А не равно В (
и А не равно В (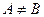 ). Если
). Если 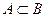 , то множество А называется собственным подмножеством множества В, а множество В — собственным надмножеством множества А.
, то множество А называется собственным подмножеством множества В, а множество В — собственным надмножеством множества А.
Покажем, что пустое множество является подмножеством любого множества А. Допустим, что утверждение  ложно, т. е. существует хотя бы один элемент х, который принадлежит множеству
ложно, т. е. существует хотя бы один элемент х, который принадлежит множеству  , который не является элементом множества А. Но множество
, который не является элементом множества А. Но множество  не имеет элементов. Значит, утверждение
не имеет элементов. Значит, утверждение  истинно.
истинно.
Пример 1.1.4
1. Множество А = {а, b, с} является собственным подмножеством множества B = {а,b,с,d,е}.
2. Множество студентов юридического факультета — подмножество множества всех студентов университета.
3. Множество четных натуральных чисел является собственным подмножеством множества всех натуральных чисел.
4. Множество натуральных чисел является подмножеством множества всех целых чисел, а множество целых чисел — подмножеством множества всех рациональных чисел.
Пусть U — некоторое множество, тогда В(U) — множество всех подмножеств множества V. В этом случае множество U называют универсальным, а множество В(U) — множеством-степенью или булеаном множества U. Например, если [U = {1,3, 5}, то В((U) = { , {1}, {3}, {5}, {1, 3}, {1, 5}, {3,5},{1,3,5}}.
, {1}, {3}, {5}, {1, 3}, {1, 5}, {3,5},{1,3,5}}.
Рассмотрим пространство 1 и определим в нем четыре операции над множествами: объединение, пересечение, разность, дополнение.
Объединением 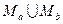 , двух множеств Мa и Мь является множество М, состоящее из элементов множества Мa и из элементов множества Мь:
, двух множеств Мa и Мь является множество М, состоящее из элементов множества Мa и из элементов множества Мь:
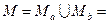 .{
.{ или
или 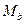 }
}
Объединением множеств А и В называется множество, в состав которого входят те и только те элементы, которые входят в состав хотя бы одного из этих множеств. Полученное множество обозначается  , т. е.
, т. е.  .
.
Пример 1.1.5
1. Пусть А = {1, 2, 3}, В = {1, 3, 4, 6}, тогда  = {1, 2, 3, 4, 6}.
= {1, 2, 3, 4, 6}.
О Пусть Ч — множество всех четных натуральных чисел, а H — множество всех нечетных натуральных чисел, тогда 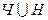 = N, где N — множество всех натуральных чисел.
= N, где N — множество всех натуральных чисел.
Пересечением  двух множеств Мa и Мь является, множество М, состоящее из элементов, которые принадлежат как множеству Мa, так и множеству Мb.
двух множеств Мa и Мь является, множество М, состоящее из элементов, которые принадлежат как множеству Мa, так и множеству Мb.
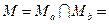 {
{ и
и 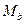 }
}
Часто союз «и» заменяют знаком &:
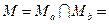 {
{ &
&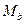 }
}
Пересечением множеств 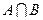 называется множество, которое состоит из элементов, входящих в состав как множества А, так и множества В. Полученное множество обозначается
называется множество, которое состоит из элементов, входящих в состав как множества А, так и множества В. Полученное множество обозначается 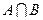 , т.е.
, т.е.  . Если
. Если  , то множества А и В называются непересекающимися.
, то множества А и В называются непересекающимися.
Пример 1.1.6
Пусть А, В, Ч, Н означают множества из предыдущего примера, тогда:
• 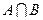 = {1,3};
= {1,3};
• 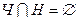 ;
;
•  ;
;
•  .
.
Пусть А — множество прямых, которые проходят через точку а некоторой плоскости, а В — множество прямых, которые проходят через точку b этой же плоскости. Тогда 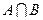 = {l}, где l — прямая, которая проходит через точки а и b.
= {l}, где l — прямая, которая проходит через точки а и b.
Операции пересечения и объединения допускают следующее обобщение. Пусть задано семейство множеств  . Тогда
. Тогда
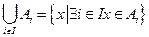
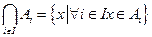
Если пересечение пустое множество  , то такие множества называются непересекающимися.
, то такие множества называются непересекающимися.
Разностью МaМb множеств Мa и Мb является множество М, состоящее из элементов, принадлежащих множеству Мa и не принадлежащих множеству Мa:
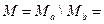 {
{ &
&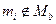 }
}
В данном случае Ма не обязательно должно являться подмножеством Ма, но если оно является подмножеством, то разность МaМb означает дополнение к Мb в Мa.
Разностью множеств А и В называется множество BА = {a | а В и а
В и а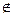 А}. Очевидно, что В А = В (
А}. Очевидно, что В А = В (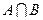 ). Если
). Если 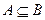 , то В А называется дополнением множества А в множестве В и обозначается А'B или просто А', когда В можно определить по контексту.
, то В А называется дополнением множества А в множестве В и обозначается А'B или просто А', когда В можно определить по контексту.
Симметрическая разность
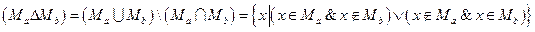 .
.
Симметричной разностью множеств А и В называется множество 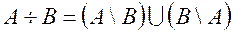 .
.
Дополнение
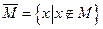 ;
;
Операция дополнения подразумевает, что задан некоторый универсум U (1): 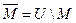 . В противном случае операция дополнения не определена.
. В противном случае операция дополнения не определена.
Двуместные операции
Введенные операции объединение, пересечение, разность, являются двуместными.
Рассмотрим операцию дополнения, являющуюся одноместной.
Дополнением (разность)  множества М является множество
множества М является множество


 Операции объединения, пересечения, разности и дополнения проиллюстрированы на рис. 1.3, а, б, в, г соответственно; результирующее множество каждой операции, изображено заштрихованной областью.
Операции объединения, пересечения, разности и дополнения проиллюстрированы на рис. 1.3, а, б, в, г соответственно; результирующее множество каждой операции, изображено заштрихованной областью.
Порядок выполнения операций
Используя эти операции, можно выражать одни множества через другие, при этом сначала выполняется одноместная операция дополнения, затем пересечения и только затем операция объединения (разности). Для изменения этого порядка в выражении используют скобки.
Пример 1.2. Рассмотрим операцию дополнения множества, являющегося пересечением множеств Мa и Мb. Ее результат совпадает с объединением дополнений этих множеств  ; в этом можно убедиться с помощью диаграмм Эйлера (рис. 1.4).
; в этом можно убедиться с помощью диаграмм Эйлера (рис. 1.4).
Таким образом, множество можно задать выражением, в которое входят идентификаторы (указатели) множеств, операции и, быть может, скобки. Такой способ задания множества называется аналитическим.
Пример 1.2.
Пусть А: = {1,2,3}, В: = {3,4,5}. Тогда 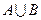 ={1,2,3,4,5},
={1,2,3,4,5}, 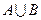 = {3}, АВ = {1,2},
= {3}, АВ = {1,2},  = {1,2,4,5}. Если определён универсум U:={0,1,2,3,4,5,6,7,8,9},то
= {1,2,4,5}. Если определён универсум U:={0,1,2,3,4,5,6,7,8,9},то  ={0,4,5,6,7,8,9},
={0,4,5,6,7,8,9},  ={0,1,2,6,7,8,9}.
={0,1,2,6,7,8,9}.
Теоретико-множественные тождества.
Законы для объединения и пересечение:
АA = А
АA = А
АВ = ВА
АВ = ВА
А(BC) = (AВ)C
А(BC) = (AВ)C
7. А (B
(B C) = (A
C) = (A В)
В) (A
(A C)
C)
8. А (B
(B C) = (A
C) = (A В)
В) (A
(A C)
C)
АU = U
10. А
 =
= 
АU = А
А= А
Законы для дополнений:
1. ненеА = А;
2. А неА =U
неА =U
3. А неА=
неА= 
4. не(А В) = неА
В) = неА неВ
неВ
5. не(А В) = неА
В) = неА неВ
неВ
6. неU = 
Законы для разностей множеств:
АВ = АВ
UА = неА
3. АU = 
А= А
5.  А =
А = 
6. АА = 
7. ((АВ)С) = А(В С)
С)
8. А(ВС) = (АВ) (А
(А С)
С)
9. А (ВС)=(А
(ВС)=(А В)(СА)
В)(СА)
10. А (ВС)=(А
(ВС)=(А В)(А
В)(А С)
С)
Каждое из написанных выше равенств, верно для любых входящих в них множеств, называют теоретико-множественными тождествами.
Существует три метода их доказательств:
- метод двух включений
- метод эквивалентных преобразований
- метод характеристической функции.
Метод двух включений является универсальным и наиболее часто применяемым методом доказательства теоретико-множественных тождеств.
Ниже приведены примеры доказательств этими методами.
Пример 1. (метод двух включений)
Докажем один из законов для дополнений:
не(А В) = неА
В) = неА неВ.
неВ.
Доказательство. (метод двух включений)
Пусть х не(А
не(А В). По определению операции дополнения это означает, что х
В). По определению операции дополнения это означает, что х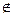 А
А В, но х
В, но х U. Следовательно, х
U. Следовательно, х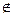 А и одновременно х
А и одновременно х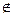 В. Таким образом, х
В. Таким образом, х неА и х
неА и х неВ. Из определения операции пересечения получаем, что х(неА
неВ. Из определения операции пересечения получаем, что х(неА неВ). Поэтому, учитывая произвольность элемента х
неВ). Поэтому, учитывая произвольность элемента х не(А
не(А В), имеем не(А
В), имеем не(А В)
В)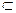 неА
неА неВ.
неВ.
Пусть теперь х неА
неА неВ. Это значит, что х
неВ. Это значит, что х неА и х
неА и х неВ. Таким образом, х
неВ. Таким образом, х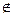 А и х
А и х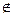 В. Поэтому х
В. Поэтому х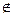 А
А В. Следовательно, х
В. Следовательно, х U (А
U (А В)= не(А
В)= не(А В). Поскольку х — произвольный элемент из неА
В). Поскольку х — произвольный элемент из неА неВ, то окончательно получаем неА
неВ, то окончательно получаем неА неВ
неВ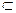 не(А
не(А В).
В).
Приходим к выводу, неА неВ=не(А
неВ=не(А В). Ч.т.д.
В). Ч.т.д.
Задание
1. Записать множество целых чисел при помощи характеристического предиката от т до п.
Ответ:

2. Записать множество натуральных чисел N при помощи порождающей процедуры
Ответ: М := {i|i := 0; for i from 0 to 9 do i := i + 1; yield i end for},
3. Доказать 
4. Доказать 
5. Дано: множества - А: = {1,2,3}, В: = {3,4,5} и универсум U:={0,1,2,3,4,5,6,7,8,9}. Определить объединение, пересечение, разность, симметрическую разность множеств АиВ, а также дополнение к этим множествам.
Покрытие и разбиение множеств
Пример. Разбиения множества А = {1, 2, 3. 4}. {1, 2}, {3, 4} и {1}, {2, 4}, {3}. Все объединения разбиений дают множество А, а все их пересечения… Если множество А представляет собой объединение подмножеств А1, А2, ..., Аn ..., то совокупность подмножеств {А1, А2,…Контрольные вопросы
1. Какие основные символы, используемые в теории множеств, вы знаете?
2. Что такое множество? Как его обозначить? Как можно задать множество? Что такое подмножество?
3. Какие основные операции выполняются над множествами?
4. Какое множество можно назвать универсальным?
5. Что такое диаграмма Эйлера-Венна? Проиллюстрируйте с помощью диаграммы Эйлера-Венна объединение и пересечение трех множеств.
6. Каковы соотношения между множествами и составными высказываниями?
7. Сформулируйте и докажите основные тождества алгебры множеств.
8. Что называется кортежем и какие кортежи называются равными?
1. Что такое счетное множество
2. Дайте определение мощности множества.
3. Чему равна мощность конечного множества
4. Какие операции можно совершать над множествами
5. Дайте определение объединения множеств
Лекция № 4
«Структуры» являются орудиями математика; каждый раз, когда он замечает, что между элементами, изучаемыми им имеют место отношения, удовлетворяющие аксиомам структуры определенного типа, он сразу может воспользоваться всем арсеналом общих теорем, относящихся к структурам этого типа, тогда как раньше он был бы должен мучительно трудиться, выковывая сам средства, необходимые для того, чтобы штурмовать рассматриваемую проблему, причем их мощность зависела бы от его личного таланта и они были бы отягчены часто излишне стеснительными предположениями, обусловленными особенностями научной проблемы.
Трубецков Д.И. Введение в синергетику. Хаос и структуры. Из эссе Ю.А. Данилова «Нелинейность» М.:Едиториал УРСС, 2004. – 240 с.
ОТНОШЕНИЯ. ОТОБРАЖЕНИЯ. СООТВЕТСТВИЯ
(лек. 2 час + прак. занят 2 час + лаб. 2 час. + самос. 2 час)
Одним из важных понятий теории множеств является понятие декартова (прямого) произведения множеств.
Декартовым (прямым) произведением M = M1 M2 …Mn множеств Mi (i = 1…n) называется множество, элементами которого являются кортежи длиной n такие, что каждая j-ая компонента есть элемент множества Mj.
Формально: M = {‹x1, x2,...xn› xj Mj, j = 1,…,n}
Бинарные отношения
AB {<a,b>|aA&bB} Таким образом, декартовым произведением множеств Мa и Мь, называется множество… Угловыми скобками < > обозначается последовательность, т. е. множество, в котором зафиксирован порядок…Свойства бинарных отношений
(а) рефлексивно, если хRхдля каждого , Отношение R на множестве Х является рефлексивным, если оно выполняется между… - прямая x параллельна прямой y в плоскости z - хRхТернарные отношения
Пример. Трехместными отношениями ТXYZ могут быть такие: 1) из х видов сырья у…N-арные отношения
Декартовым произведением Х1Х2... Хn п множеств Х1,Х2, ... ,Хn называется множество всех упорядоченных п-ок <х1, х2,..., xn>, составленных из… В том случае, если M1 = M2 =…= Mn, то пишут Mn. Часто Mn называют… Декартовым произведениемОтображения
По количеству элементов, между которыми определены связи, отношения делятся на унарные (одноместные), бинарные (двухместные), тернарные… В бинарных отношениях участвуют пары элементов множеств, так называемые…Соответствие
Формально S M. Частные случаи. 1. Если n = 2, то говорят о бинарном соответствии S M1 M2.Функция
Пусть Х — некоторое множество на числовой оси. Говорят, что на этом множестве определена функция f, если каждому числу хХ поставлено в… На рис. 5, в качестве примера, изображена функция у=|х|. Область определения… Переменную х называютаргументом функции, а у — еезначением. Значок f интерпретируется, как правило, преобразования…Представление функции в терминах отношений
Подмножество , называется функцией, если для каждого элемента , найдется не более одного элемента вида ; при этом если для каждого элемента х… Множество Мx образует область определения функции F, множество Му — область… Пусть X, Y - некоторые множества. Говорят, что задана функция (отображения), действующая из множества X во множество…У = F(х1, х2, . . . , хn).
Две функции f и g равны, если они состоят из одних и тех же элементов. Область определения функции и область ее значений задается так же, как и для бинарных отношений. Если область определения дf = Х и область значений сf 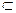 Y, то говорят, что функция f задана на множестве Х со значениями во множестве Y, при этом f отображает множество Х во множество Y. Это отображение обозначается как f: Х
Y, то говорят, что функция f задана на множестве Х со значениями во множестве Y, при этом f отображает множество Х во множество Y. Это отображение обозначается как f: Х 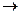 Y.
Y.
Если f — функция, то вместо  пишут y = f(х) и говорят, что y — значение, соответствующее аргументу х, или у — образ элемента х при отображении f. При этом х называют прообразом элемента у.
пишут y = f(х) и говорят, что y — значение, соответствующее аргументу х, или у — образ элемента х при отображении f. При этом х называют прообразом элемента у.
Назовем f — n-местной функцией из Х в Y, если f: Х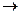 Y. Тогда записываем y = f(х1, … хn) и говорим, что у — значение функции при значении аргументов х1, … хn.
Y. Тогда записываем y = f(х1, … хn) и говорим, что у — значение функции при значении аргументов х1, … хn.
Если функция (отображение) f сопоставляет каждому элементу 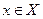 элемент
элемент 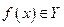 , то будем писать f: Х
, то будем писать f: Х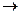 Y (такая функция может трактоваться как отношение
Y (такая функция может трактоваться как отношение 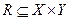 с тем свойством, что для каждого
с тем свойством, что для каждого 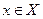 существует в R точно одна пара вида <х,y>,
существует в R точно одна пара вида <х,y>,  ; для наших же целей достаточно интуитивного понятия функции).
; для наших же целей достаточно интуитивного понятия функции).
Отношение R Х
Х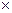 Y, т.е. множество упорядоченных пар <х,у>, х
Y, т.е. множество упорядоченных пар <х,у>, х X, у
X, у Y называется функцией тогда и только тогда, когда первые элементы этих пар не повторяются.
Y называется функцией тогда и только тогда, когда первые элементы этих пар не повторяются.
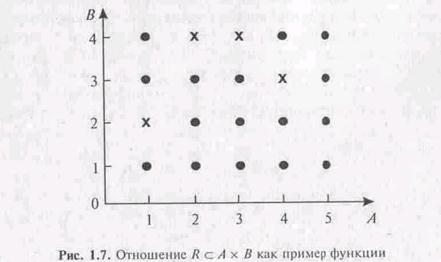
Пример. Отношение не является функцией, так как оно представлено следующими парами: <1,2>, <1,3>, <2,3>, <2,4>, <3,3>, <3,4>, <4,2>, <4,3>. Примером функции на том же декартовом произведении является отношение <1,2>,<2,4>, <3,4>, <4,3>.
Требование неповторяемости первых элементов упорядоченных пар, представляющих отношение, гарантирует однозначность отображения, т.е. функцию f: Х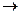 Y.
Y.
Функции, функционалы, операторы
В зависимости от того, какой характер имеют множества задания функций Х и множества ее значений Y, выделяют функции числовые (Х и Y — числовые множества), функционалы (множество Х — любой природы, а множество Y — числовое), операторы (множества X, Y — любой природы).
Пример. 1. Числовых функций являются все элементарные функции, например, у = х2, у =logх, у = sinх и т.д., а также их суперпозиции.
2. Функционал. Пусть в некотором городе N между двумя пунктами А и В имеется множество дорог X, каждой из которой поставлено в соответствие время t Т передвижения по ней автомобиля. Тогда множество пар <х,t>, х
Т передвижения по ней автомобиля. Тогда множество пар <х,t>, х X, t
X, t T — функционал от t, определенный на множестве X.
T — функционал от t, определенный на множестве X.
3. Примером оператора может быть телефонная книга, в которой каждой фамилии абонента поставлен в соответствие один и только один номер его телефона.
Инъекция, сюръекция, биекция
В том случае, когда Х отображается на некоторое собственное подмножество YсY, — это отображение Х в Y. В противном случае, т.е. когда Yс=Y, — это отображение Х на Y. Оно называется… Если для любых двух различных х1, и х2 функции f(x1) и f(x2) также различны, такая функция f называется инъективной. …Суперпозиция бинарных отношений
Если f: Х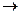 Y, а g: Y
Y, а g: Y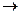 Z, то функция F: X
Z, то функция F: X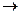 Z, определенная для каждого
Z, определенная для каждого 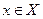 формулой F(х) = g(f(х)), называется композицией (суперпозицией) функции f и g, илисложной функцией.
формулой F(х) = g(f(х)), называется композицией (суперпозицией) функции f и g, илисложной функцией.
Обратная функция
Если f(А) = Y, то будем говорить о функции из Х на Y. Функция f:Х→Y называется обратимой (взаимно однозначной), если для произвольных а ≠ b → f(а) ≠ f(b).Пусть задана функция f: Х Y и сf —… Обратная функция f-1 ставит в соответствие каждому элементу f его прообраз f-1(y), т.е. некоторое множество элементов.…Классификация отображений
Пусть X и Y - два частично упорядоченных множества.
Отображение ζ множеств X на Y есть изоморфизм (или изоморфное отображение), если оно взаимно однозначно и сохраняет порядок, то есть неравенства х ≤ у и ζ (х) ≤ ζ (у) равносильны.
Обратное отображение ζ -1 есть также изоморфизм.
В случае существования изоморфизма частично упорядоченные множества называются изоморфными. Изоморфные частично упорядоченные множества обычно отождествляют, поскольку с точки зрения свойств, связанных с порядком, они неразличимы.
Отображение ц называется изотопным, если неравенство х ≤ у влечет ζ (х) ≤ ζ (у). Изоморфное отображение всегда изотонно (но не наоборот!).
Взаимно однозначное отображение ω множества X на Y называется дуальным изоморфизмом, если равносильны неравенства х ≤ у и ζ (х) ≥ ζ (у). Если такое отображение существует, то говорят, что X и Y дуально изоморфны.
Операция
Частным случаем п-местной функции у = F(х1, х2, . . . , хn) является п-местная операция. Под п-местной операцией On в множестве М понимается п-местная функция у = F(х1, х2, . . . , хn), у которой области определения аргументов и область значений функции совпадают:М1 = М2 = ... = Мn = Му. Таким образом, п-местная операция по п элементам множества М определяет (п + 1)-й элемент этого жемножества.
Алгебраической n-арной (n-местной) операцией на множестве M называется n-местная функция у = f(x1,x2,...,xn), у которой область определения аргументов xi и область значений функции совпадают (n  N).
N).
Пояснение.
1. Тот факт, что алгебраическая операция является частным случаем бинарного однозначного соответствия, отражается в её формальной записи f: Mn 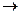 M., т.е.:
M., т.е.:
2. Поскольку алгебраическая операция по n элементам множества M определяет (n+1) элемент этого же множества M, то n-местную алгебраическую операцию можно рассматривать и как (n+1)-арное однозначное отношение на множестве M.
3. Если f: M 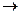 M, то говорят об унарной (одноместной) алгебраической операции; если f: M2
M, то говорят об унарной (одноместной) алгебраической операции; если f: M2 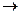 M, то имеют в виду бинарную (двухместную) алгебраическую операцию.
M, то имеют в виду бинарную (двухместную) алгебраическую операцию.
Частично упорядоченные множества
Частичным упорядочением (частичным порядком) в непустом множестве X называется всякое подмножество множества , удовлетворяющее следующим аксиомам: … I. При любом справедливо - рефлексивность отношений. II. Если и , то y = x - антисимметричность отношений.Минимизации представления множества
Под сложностью представления множества Мбудем понимать число символов Мi, неМi, в задающем его выражении. Пусть в пространстве 1 = {М1, М2, М3} задано множество вида М(М1, М2, М3) = неМ1неМ2неМ3неМ1неМ2М3неМ1М2неМ3М1неМ2неМ3М1М2неМ3М1М2М3 сложность которого равна 18.ЭЛЕМЕНТЫ КОМБИНАТОРИКИ
(лек. 2 час + прак. занят 2 час + лаб. 4 час. + самос. 12 час)
Комбинаторика – это раздел математики, изучающий свойства объектов, составленных из конечного множества. Комбинаторную математику часто называют комбинаторным анализом или комбинаторикой.
Типичными задачами комбинаторики являются такие разделы как перестановки, разбиения множеств и чисел, биномиальные коэффициенты, производящие функции и т.д., а также алгоритмы генерирования упомянутых комбинаторных объектов. Классической задачей комбинаторики является задача определения числа способов размещения в каком-то количестве «ящиков» так, чтобы были выполнены некоторые условия. Комбинаторика имеет дело с конечными множествами, поэтому ее и называют иногда теорией конечных множеств.
Основные правила комбинаторики
Правило произведения. Пусть имеем декартово произведение двух множеств {a,b,c}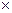 {1,2,3,4}. Число элементов, которого равно произведению числа элементов первого множества на число элементов второго множества, в дано случае это будет 3
{1,2,3,4}. Число элементов, которого равно произведению числа элементов первого множества на число элементов второго множества, в дано случае это будет 3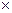 4 = 12. В общем случае можно сформулировать правило произведения:
4 = 12. В общем случае можно сформулировать правило произведения:
Если требуется выполнить последовательно k независимых операций, и каждая может быть выполнена ni (i =1,2, ,k) способами, то общее число исходов равно их произведению n = n1 n2 ... nk.
Число элементов декартова произведения (мощность) n сомножителей равно произведению числа элементов (мощности) каждого из этих сомножителей.
Правило сумм.
Если элемент x может быть выбран m способами, а элемент y - n способами, то выбор, либо x, либо y может осуществляться m + n способами.
Перечислительная комбинаторика
К перечислительной комбинаторике относятся задачи поиска числа способов построения кортежей из элементов конечного множества, как с разными, так и одинаковыми. Простейшими кортежами являются перестановки, размещения и сочетания.
Пусть A – конечное множество, состоящее из n элементов, т.е. мощность этого множества │A│ = card A = n.
Перестановки
Перестановкой элементов множества A называется любой кортеж <a1, a2, …, an> состоящий из n различных элементов множества A. Построим кортежи из этого множества A длиной n. Кортежи будут отличаться друг… Число перестановок определим исходя из следующего рассуждения. На первом месте в кортеже можно поставить любой из n…Перестановки с повторениями
Пример. Сколько слов можно получить, переставляя буквы в слове «МАТЕМАТИКА»Т|п = т!/п!
|т|п = |т + п-1|п
Размещения
Схема выбора состоит в выборе k элементов из n-элементного множества без возвращения. Для этого необходимо совершить k действий: первое действие… Отличие размещения от перестановки. Если размещения отличаются друг от друга только порядком, так как в каждом из них…Размещения с повторениями
Пример. Сколько пятизначных телефонных номеров можно составить из элементов множества {0,1,2,3,4,5,6,7,8,9}.Упорядоченное размещение
Теорема 1.4. Число упорядоченных размещений n объектов по т ящикам равно |т|п = т (т+1) . . . (т+ n-1) (полагаем |т|0 = 1).Сочетания
Сочетание отличается от размещения тем, что в нем не учитывается порядок. Поэтому каждому сочетанию соответствует k! размещений. Сочетания из m подмножеств n-элементного множества, на элементах которых задан… Anm = m!CnmСочетания с повторениями
Пример. Сколько наборов из 7 товаров можно составить, если имеется всего 4 вида.Бином Ньютона
Из элементарной математики хорошо известны формулы сокращенного умножения:
А+b)2 =а2 +2аb+b2 и (а+b)з=аз+За2 b + Заb2 + bЗ.
Число всех k–элементных подмножеств n-элементного множества будем обозначать  . Символ
. Символ  называется биномиальным коэффициентом, исходя из следующей формулы для n-й степени бинома (x+y).
называется биномиальным коэффициентом, исходя из следующей формулы для n-й степени бинома (x+y).
(x+y)n = У xk yn-k
xk yn-k
Чтобы убедится в истинности этой формулы, достаточно заметить, что коэффициент при xk yn-k равен числу способов которыми из n сомножителей (x+y) можно выбрать k сомножителей.
С числами 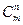 связано функциональное тождество, называемое формулой бинома Ньютона. Из элементарной математики хорошо известны формулы сокращенного умножения:'
связано функциональное тождество, называемое формулой бинома Ньютона. Из элементарной математики хорошо известны формулы сокращенного умножения:'
(а + b)2 = а2+ 2аb +b2, (а + b)3 = а3 + За2 b + Заb2 + b3.
Эти формулы можно записать так:
(a + b)2 = (C02 a2 b0 + C12 аb + C02 а0 b2;
(а + b)3 = C02 a3 b0 + C13 а2 b1 + C23 а1 b2 + C33 а0 b3.
Имеет место и общая закономерность: справедливо равенство:
(а + b)n = C0n аn b0 + C1n аn-1 b1 + C2n аn-2 b2 + ... + Cnn а0 bn.
Это равенство и называется биномом Ньютона, а коэффициенты C0n, C1n, C2n,..., Cnn называются биномиальными коэффициентами.
Если положить, а = b = 1, то из формулы бинома Ньютона вытекает следующее важное соотношение: (1 + 1)n = C0n + C1n + C2n + ... + Cnn = 2n - формула суммы биномиальных коэффициентов.
Если положить в биноме Ньютона а =1, b = -1,то
C0n - C1n + C2n - ... +(-1)n Cnn = 0 .
Поскольку 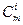 =
= 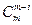 , то биномиальные коэффициенты, равноотстоящие от концов в формуле бинома Ньютона, равны.
, то биномиальные коэффициенты, равноотстоящие от концов в формуле бинома Ньютона, равны.
Все свойства хорошо просматриваются из треугольника Паскаля.
0 1
1 1 1
2 1 2 1
3 1 3 3 1
4 1 4 6 4 1
5 1 5 10 10 5 1
6 1 6 15 20 15 6 1
7 1 7 21 35 35 21 7 1
8 1 8 28 56 70 56 28 8 1
Разбиения. Комбинаторные числа Стирлинга и Белла
Пусть card(M) = n и k — число непустых подмножеств, на которые разбивается множество M. Рассмотрим разбиение множества M = {а1, а2, аn}. Обозначим через S(n,k) - число разбиений множества на k (n>0, 0<k≤n) непустых частей, а через B(n) – число всех разбиений множества M(n>0) на непустые части.
Тогда S(n,k) будем называть число способов разбить множество M мощностью n на k непустых множества.
S(0,0) = 1
S(n,0) = 0n≠1
Числа S(n,k) называются числами Стирлинга.
Числа Стирлинга:
| nk | |||||||
| - | - | - | - | - | - | ||
| - | - | - | - | - | |||
| - | - | - | - | ||||
| - | - | - | |||||
| - | - | ||||||
| - | |||||||
Найдем явную формулу для чисел S(n,k). Каждое разбиение M = E1 E2
E2 . . .
. . .  Ek на непустые подмножества можно характеризовать набором чисел (l1, l2, . . . .,ln ), где
Ek на непустые подмножества можно характеризовать набором чисел (l1, l2, . . . .,ln ), где
l1 — число подмножеств разбиения мощности 1,
l2 — число подмножеств разбиения мощности 2,
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ,
Ln - число подмножеств разбиения мощности n.
Эти числа удовлетворяют тождеству
L1 + 2 l2 + . . . . + n ln = n.
Теорема 3.
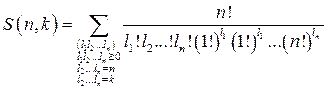
Доказательство.
Процесс построения всех разбиений множества Mна k непустых частей, характеризуемых набором чисел (l1, l2, . . . ., ln), l1 + l2 + . . . . + ln = k, можно представить следующим образом.
Возьмем п упорядоченных ячеек и разобьем их на k; подмножеств, характеризуемых данным набором чисел (l1, l2, . . . ., ln). Эти подмножества занумеруем числами 0, 1, ..., k - 1. Разместим в этих ячейках элементы а1, ..., aп. Очевидно, что разбиение ячеек на подмножества структуры (l1, l2, . . . ., ln) порождает разбиение элементов а1, ..., aп на подмножества такой же структуры. Последнее задается набором (б1, б2, ..., бп), где бi — номер подмножества разбиения ячеек, которому принадлежит элемент бi Производя различные размещения элементов а1, ..., aп, по ячейкам, получим все разбиения множества M на k непустых частей данной структуры (l1, l2, . . . ., ln). При этом два размещения определяют одно и то же разбиение множества M тогда и только тогда, когда для соответствующих им наборов (б1, б2, ..., бп) и (б1, б2, ..., бп) выполнено условие
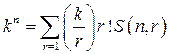
Если сравнить соответствующие слагаемые в (15) и (18), то можно увидеть, что они выражают одно и то же число. Отсюда получаем еще одно явное выражение для S(n,r) (n, r>0)
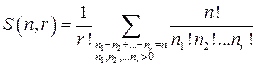
Эта формула не пригодна для практических вычислений S(n,k), так как она предполагает знание всех решений уравнения (14) или (17).
Эффективный способ вычисления чисел Стирлинга 2-го рода и изучение их свойств связано с установлением ряда реккурентных соотношений для S(n,k).
Теорема. S(m,n) = S(m-1,n-1) + n S(m-1,n)
Комбинаторные числа можно изучать двумя способами: теоретико-множественным и алгебраическим.
Числа Стирлинга 2-го рода (Джеймс Стирлинг (1699-1770))
Комбинаторные числа S(n,k) называются числа Стирлинга 2-го рода, а комбинаторные числа B(n) - числами Белла. Эти числа связаны соотношением:

Число разбиений m-элементного множества на n блоков называется числом Стирлинга второго рода и обозначаются S(m,n)
Найдем явную формулу для определения чисел Стирлинга 2-го рода S(n,k).
По определению
S(m,0) = 0 при m > 0
S(m, m) = 1
S(0, 0) = 1
S(m,n) = 0 при n > m
Числа Стирлинга 1-го рода
Число сюръективных функций, то есть число размещений m предметов по n ящикам, таких, что все ящики заняты, называется числом Стирлинга первого рода и обозначаются s(m,n).
Число Белла (Эрик Темпл Белл (1883-1960))
Число всех разбиений m-элементного множества называется числом Белла и обозначается B(m):
Числа Белла:
B(0) = 1
B(1) = 1
B(2) = 2
B(3) = 5
B(4) = 15
B(5) = 52
B(6) = 203
Также существуют число Белла B(n), которое означает число всевозможных вариантов разбиения множества M на непустые подмножества.
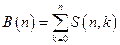 )
)
Утверждение 1. Для определения S (n,k) существует рекуррентная формула S(n,k) = S(n-1,k-1)+ k S(n-1,k).
Доказательство.
M: card (M) = n
M = {a1,a2,…,an}
M {an}
Существует два способа присоединения {an} к M:
1) Пусть M было разбито на k-1 непустых подмножества, тогда {an} можно было бы присоединить отдельным k-м подмножеством.
2) Множество M {an} было разбито на k непустых подмножества, тогда элемент {an} можно было бы присоединить к любому из уже существующих подмножеств. Всего k вариантов.
Метод производящий функций
Исходным пунктом являются последовательность {ai} комбинаторных чисел и последовательность функций {φi(x)} (i = 0, 1, …). Рассмотрим ряд ,X-x2)F(x) =1
Отсюда находим явный вид производящей функции F(x):

Решая уравнение x2 + x – 1 = 0 находим его корни

Найдем разложение F(x) на элементарные дроби
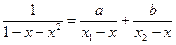
Имеем ax2 + bx1 – (a + b)x = -1
Это справедливо, если a = - b и 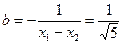 .
.
Далее, воспользовавшись формулой для суммы убывающей геометрической прогрессии (при 
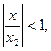 ) получим
) получим
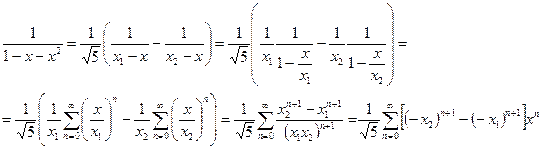
откуда
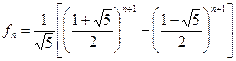
что дает явное выражение для чисел Фибоначчи.
Контрольные вопросы
1. Что такое комбинаторика и для чего она нужна?
2. Что называется:
— перестановкой п-элементного множества;
— размещением из п элементов по т элементов;
— сочетанием из п элементов по т элементов?
3. В чем отличие размещений от перестановок?
4. В чем отличие сочетаний от размещений?
5. Сколькими способами можно разместить три книги на книжной полке?
6. Запишите формулу для вычисления числа сочетаний элементов, используемую в формуле бинома Ньютона.
7. Как найти число перестановок с повторениями?
8. Сколько существует пятизначных чисел, у которых каждая следующая цифра:
—меньше предыдущей,
— больше предыдущей.
9. Сколько прямых можно провести через п точек, если никакие три из них не лежат на одной прямой?
10. Сколько разных слов можно составить перестановкой букв в слове «чачача»?
11. Вычислите: (а + b + с)2; (а + b + с)3.
12. Покажите, что сумма  делится на р, где р — простое число.
делится на р, где р — простое число.
13. Докажите свойства биномиальных коэффициентов.
14. Какая разница между декартовым квадратом некоторого непустого множества A и множеством всех двухэлементных подмножеств множества A?
15. Сколько отношений эквивалентности можно построить на множестве, которое состоит из двух, трех, четырех элементов? Сколько бинарных отношений можно задать на множестве из п элементов?
16. Сколько существует функций из множества A в множество В, если А = т, а |B| = n?
Лекция № 6
В самой математике главные средства достигнуть истины – индукция и аналогия.
Лаплас, Опыт философии теории вероятностей, М., 1908, стр.7.
АЛГЕБРАИЧЕСКАЯ СИСТЕМА
Алгебраическая система
Пояснение. 1. Множество M алгебраической системы A называют несущим, или основным… 2. Совокупность алгебраических операций и отношений алгебраической системы называют сигнатурой Σ. В этом случае…Замыкание и подалгебры
Если X замкнуто относительно всех , то называется подалгеброй алгебры , где ,… Пример 1. Алгебра - поле действительных чисел.Морфизмы
Из вышеприведенных определений следует, что каждая алгебраическая структура выделяет класс отображений между объектами с данной структурой, согласованных с операциями этой структуры.
Такие отображения называются морфизмами. Изоморфизм множеств был рассмотрен выше.
Гомоморфизмы
Алгебры с различными типами имеют различное строение. Пусть A =  и B =
и B =  - две алгебры одинакового типа. Если существует f: A → B, такая что
- две алгебры одинакового типа. Если существует f: A → B, такая что
 ,
,
то говорят, что f - гомоморфизм из A в B (гомоморфизм «уважает» операции)
Пусть A = 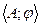 , B =
, B = 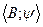 , тип = (1) и f: A → B. Действие этих функций изобразим с помощью следующей диаграммы:
, тип = (1) и f: A → B. Действие этих функций изобразим с помощью следующей диаграммы:
φ
A → A
F↓ ↓f
B → B
Пусть f –гомоморфизм. Если взять конкретное  и двигаться по двум различным путям на диаграмме, то получится один и тот же элемент
и двигаться по двум различным путям на диаграмме, то получится один и тот же элемент 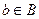 (так как f(φ(a)) = ψ(f(a))), т.е. диаграмма коммутативна. Коммутативной диаграмма называется потому, что условие гомоморфизма можно переписать так
(так как f(φ(a)) = ψ(f(a))), т.е. диаграмма коммутативна. Коммутативной диаграмма называется потому, что условие гомоморфизма можно переписать так
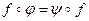
где  - суперпозиция функций.
- суперпозиция функций.
Рассмотрим морфизмы с другой стороны.
Пусть даны алгебраические системы A =  , B =
, B =  . Отображение φ: A → B называется гомоморфизмом системы A в систему B, если выполняются следующие условия:
. Отображение φ: A → B называется гомоморфизмом системы A в систему B, если выполняются следующие условия:
1) для любого функционального символа f(n)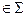 ,соответствующих функций fАи fВ в системах A и B и любых a1, a2, …,
,соответствующих функций fАи fВ в системах A и B и любых a1, a2, …,  выполняется
выполняется
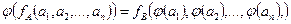
2) для любого предикатного символа  соответствующих предикатов PАи PВв системах A и B и любых a1, a2, …,an
соответствующих предикатов PАи PВв системах A и B и любых a1, a2, …,an  выполняется
выполняется

Если φ: A → B – гомоморфизм , то будем его обозначать φ:A→B
При гомоморфизме сохраняются действий операций и отношения. Это позволяет переносить изучение свойств с одной системы на другую.
Пример. Пусть A = 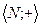 , B =
, B = 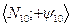 , где N10 +{0,1,2,3,4,5,6,7,8,9}, а +10 - сложение по модулю 10. Тогда f:=a mod 10 - гомоморфизм из A в B.
, где N10 +{0,1,2,3,4,5,6,7,8,9}, а +10 - сложение по модулю 10. Тогда f:=a mod 10 - гомоморфизм из A в B.
Гомоморфизм, обладающий дополнительными свойствами, имеют специальные названия.
Гомоморфизм, который является инъекцией, называется мономорфизмом.
Гомоморфизм, который является сюръекцией, называется эпиморфизмом.
Гомоморфизм, который является биекцией, называется изоморфизмом.
Если A = B, то гомоморфизм называется эндоморфизмом, а изоморфизм называется автоморфизмом.
Фундаментальные алгебры
На множестве М может быть задано много различных операций. Чтобы выделить одну из них используют обычно скобки <М, *> и говорят, что операция * определяет на М алгебраическую структуру. Так, например, на множестве целых чисел помимо хорошо известных операций сложения и умножения целых чисел n и m можно ввести много других, например, операцию ○ суть которой состоит в следующем m○n = n m - 3n и т.п.
В зависимости от операции получаем различные алгебраические структуры: <М, *>; <М, +>; <М, х>; <М, ○>. Это бинарные операции, но операции могут быть в общем случае n–арными: при n = 1 – унарные, при n = 2 – бинарные, при n = 3 – тернарные и т.д. и их комбинации. Такие алгебраические структуры составляют специальную теорию универсальных алгебр. Изучение в общем виде алгебр для нас не представляет практического интереса, поэтому рассмотрим наиболее часто используемые алгебры, т.е. фундаментальные алгебры.
Подведем итог сказанному. Алгебра A =  – это совокупность A носителя и сигнатуры Σ. Носитель A – это множество, которое может состоять из нескольких множеств, тогда алгебра будет называться многоосновной. Сигнатура Σ также является множеством, элементами которого являются множества {F1,i1 , F2,i2 , …,Fn,in,}, где первый индекс указывает местность операции, а второй индекс указывает порядковый номер, например, операции F2,i2 – бинарные операции, номер данной операции i2, где i2 принимает значения 1, 2, …, n2.
– это совокупность A носителя и сигнатуры Σ. Носитель A – это множество, которое может состоять из нескольких множеств, тогда алгебра будет называться многоосновной. Сигнатура Σ также является множеством, элементами которого являются множества {F1,i1 , F2,i2 , …,Fn,in,}, где первый индекс указывает местность операции, а второй индекс указывает порядковый номер, например, операции F2,i2 – бинарные операции, номер данной операции i2, где i2 принимает значения 1, 2, …, n2.
Алгебры с унарными операциями
Самые простые алгебры A =  – это алгебры с унарными операциями F1,i1, где i1 принимает значения 1, 2, …, n1. Эти операции определяют свойства элементов и самой простой алгеброй будет алгебра, когда i1 = 1, т.е. A =
– это алгебры с унарными операциями F1,i1, где i1 принимает значения 1, 2, …, n1. Эти операции определяют свойства элементов и самой простой алгеброй будет алгебра, когда i1 = 1, т.е. A = 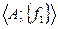 .
.
Алгебры с бинарными операциями
Бинарные алгебры имеют вид A =  – это алгебры с бинарными операциями F2,i2, где i2 принимает значения 1, 2, …, n2. Из этих алгебр самой простой будут алгебры с одной бинарной операцией, т.е. A =
– это алгебры с бинарными операциями F2,i2, где i2 принимает значения 1, 2, …, n2. Из этих алгебр самой простой будут алгебры с одной бинарной операцией, т.е. A = 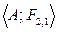 , где A = M
, где A = M M, а F2,1 =*, т.е. *: M
M, а F2,1 =*, т.е. *: M M → M. Рассмотрим более подробно эти алгебры.
M → M. Рассмотрим более подробно эти алгебры.
Алгебры с одной бинарной операцией
Бинарная операция * на множестве М называется ассоциативной, если a*(b*c) = (a*b)*c для всех a, b, c принадлежащих множеству М. Бинарная операция * на множестве М называется коммутативной, если a*b = b*a… Пример.M*n)*p = -(m*n) – p = -(- m - n) – p = m + n – p
Таким образом m*(n*p) ≠ (m*n)*p, т.е. эта алгебраическая структура не ассоциативна.
2. Рассмотрим множество Мn(R) всех квадратных матриц порядка n>1 на котором задана операция умножения Ч в обычном смысле. Так построенная алгебраическая структура ассоциативна, но не коммутативна. (докажите)
Названия свойств операций будут присваиваться и соответствующим алгебраическим структурам <М, *>, т.е. коммутативная или ассоциативная алгебраическая система или то и другое одновременно.
Рассмотрим еще один элемент e множества М, который может быть только один, если он существует на данной алгебраической структуре. Этот элемент e называется нейтральным или единичным. Он обладает свойствами: во-первых, e  М, а во-вторых, для любого элемента m
М, а во-вторых, для любого элемента m  М выполняется равенство – 'e*М = М*e' = М, где 'e,e' - соответственно левый и правый нейтральный элемент.
М выполняется равенство – 'e*М = М*e' = М, где 'e,e' - соответственно левый и правый нейтральный элемент.
Полугруппа
Множество М с заданной на нем бинарной ассоциативной операцией f2 называется полугруппой <М, f2>. Пусть S полугруппа на алгебраической структуре с f2 ≡ *. Подмножество S' 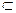 S называется подполугруппой, если а*b
S называется подполугруппой, если а*b  S' для всех а,b
S' для всех а,b  S', тогда подмножество S' замкнуто относительно операции *. Для полугруппы для любых a, b, c принадлежащих М выполняется для бинарной операции условие
S', тогда подмножество S' замкнуто относительно операции *. Для полугруппы для любых a, b, c принадлежащих М выполняется для бинарной операции условие
A * (b * c) = (a * b) * c
Пример 1. Множество непустых слов A+ в алфавите A образует полугруппу относительно бинарной операции конкатенации.
Пример 2. Любое множество функций, замкнутое относительно суперпозиции, образует полугруппу.
Если в полугруппе существует система образующих, состоящая из одного элемента, то такая полугруппа называется циклической.
Пример 1. <N, +> является циклической полугруппой, поскольку {1} является системой образующих, т.е каждое натуральное число можно представить, как последовательность знаков 1. Различные слова в алфавите {1} это различные элементы носителя, то есть эта полугруппа свободна.
Теорема (Маркова-Поста). Существует полугруппа, в которой проблема распознования равенства слов алгоритмически неразрешима.
Моноид
Полугруппа с единичным (нейтральным элементом) принято называть моноидом или просто полугруппой с единицей. Мощность моноида, как множества обозначается |М| или Card М.
Моноид – это полугруппа с единицей. 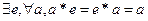
Теорема. Единица моноида единственна.
Доказательство. Пусть 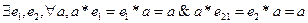 . Тогда
. Тогда 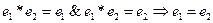
Теорема. Всякий моноид над М изоморфен некоторому моноиду преобразований над М.
Доказательство. Пусть М = <М, *> - моноид над М = {e,a,b,c, ….}. Построим . Тогда 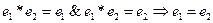
Группоид
Если f2 — операция типа умножения (), то группоид называют мультипликативным, если f2 - операция типа сложения (+), то аддитивным. Пусть А = <М, f2) — группоид; обозначим операцию f2 как . Тогда элемент… Никакой группоид не может иметь более одного нейтрального элемента. Действительно, еслиТе = ет = т и те'=е'т=т
справедливо для всех 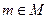 , то
, то
е' = е' е = е.
е = е.
Если группоид <М, > мультипликативный, то нейтральный элемент называется единицей и обозначается 1; если аддитивный, то нейтральный элемент называется нулем и обозначается 0.
> мультипликативный, то нейтральный элемент называется единицей и обозначается 1; если аддитивный, то нейтральный элемент называется нулем и обозначается 0.
Группоид А = <М, > называется идемпотентным, если его сигнатура удовлетворяет закону идемпотентности
> называется идемпотентным, если его сигнатура удовлетворяет закону идемпотентности
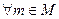
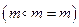 .
.
Группоид <М, >, сигнатура которого удовлетворяет закону коммутативности
>, сигнатура которого удовлетворяет закону коммутативности
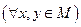
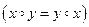 .
.
называется коммутативным или абелевым.
Группоид <М, >, в котором выполняется закон ассоциативности
>, в котором выполняется закон ассоциативности 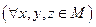
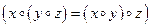 называется ассоциативным или полугруппой.
называется ассоциативным или полугруппой.
Группа
Полугруппа <М, > в которой выполнимы обратные операции: для любых
> в которой выполнимы обратные операции: для любых  каждое из уравнений
каждое из уравнений 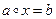 ,
,  обладает единственным решением, называется группой.
обладает единственным решением, называется группой.
Пример.
Рассмотрим понятие группы на примере группы подстановок, содержащей шесть элементов. Группу подстановок исследовал выдающийся французский математик Галуа в связи с решением уравнений в радикалах.
Подстановкой n-й степени называется взаимно однозначное отображение множества из п элементов на себя.
Рассмотрим три элемента: х1, х2, х3. Существует шесть перестановок из трех элементов (3! = 6): х1х2х3, х2х3х1, х1х2х3, х3х1х2, х2х1х3, х3х2х1. Запишем две перестановки из трех элементов друг под другом:
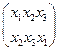
Эта запись означает, что х1 переходит в х2, х2 - в х3, х3 – в х1.
Число возможных подстановок равно числу перестановок. Введем следующие обозначения для шести возможных подстановок:


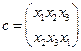


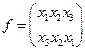
Введем операцию умножения  над подстановками.
над подстановками.
Произведением подстановок называется подстановка, получаемая в результате последовательного выполнения сначала первой, а затем второй из перемноженных подстановок. Например,

Выражение б в, б,в = а, b, с, d, е, f определяет табл. 1.1.
в, б,в = а, b, с, d, е, f определяет табл. 1.1.
Таблица 1.1
| б | в | |||||
| а | b | с | d | е | f | |
| a | а | b | с | d | е | f |
| b | b | а | d | с | f | е |
| c | с | е | а | f | b | d |
| d | d | f | b | е | а | с |
| е | е | с | f | а | d | b |
| f | f | d | е | b | с | а |
В рассматриваемой алгебре <М,  > выполняется закон ассоциативности, но не выполняется закон коммутативности.
> выполняется закон ассоциативности, но не выполняется закон коммутативности.
Абелева группа
Группа с коммутативной операцией называется коммутативной, но чаще ее называют абелевой в честь норвежского математика Абеля. Термин «группа» ввел французский математик Галуа, который и является создателем теории групп.
Алгебра с двумя операциями
Рассмотрим алгебраические структуры с двумя операциями. Эти структуры нашли широкое применение при решении практических задач.
Кольца
Алгебра <М,  , +>, которая по умножению является мультипликативным группоидом, по сложению — абелевой группой, причем умножение связано со сложением законами дистрибутивности
, +>, которая по умножению является мультипликативным группоидом, по сложению — абелевой группой, причем умножение связано со сложением законами дистрибутивности
а (b + с) = а
(b + с) = а b + a
b + a с,
с,
(b + с)  а = b
а = b а + с
а + с а,
а,
называется кольцом.
Тело
Кольцо, в котором все отличные от нуля элементы составляют группу по умножению, называется телом.
Поля
Тело, у которого мультипликативная группа абелева, называется полем.
Отношения
Фундаментальным понятием дискретной математики является понятие отношения, которое используют для обозначения связи между объектами или понятиями.
Квадратом множества М называется декартово произведение двух равных между собой множеств: М М = М2. Бинарным отношением Т в множестве М называется подмножество его квадрата:
М = М2. Бинарным отношением Т в множестве М называется подмножество его квадрата: 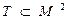 . Элементы тi, и тj, находятся в отношении T, если
. Элементы тi, и тj, находятся в отношении T, если 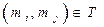 .
.
Граф
Совокупность множества М с заданным в нем бинарным отношением 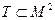 называется графомG:
называется графомG:
 ,
,
где М - носитель графа (множество вершин); Т - сигнатура графа (множество дуг).
Рассмотрим задание бинарного отношения с помощью матрицы смежности и фактор-множества.
Матрица смежности
При матричном задании используют двумерную таблицу — матрицу смежности, каждой строке (столбцу) которой взаимно однозначно сопоставляют элемент множества М. Тогда каждая клетка (i, j) взаимно однозначно соответствует элементам множества М2. Клетку (i, j), которая соответствует элементу, принадлежащему 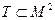 , как-то отличают, например зачерняют или помещают в нее единицу; остальные клетки оставляют незачерненными или записывают в них нули.
, как-то отличают, например зачерняют или помещают в нее единицу; остальные клетки оставляют незачерненными или записывают в них нули.
Пример.
Рассмотрим предложенную фон Нейманом блок-схему ЭВМ, которая состоит из множества устройств
Фактор-множества и фактор-алгебра
Здесь есть подмножество элементов множества M эквивалентных x , называемых… Из определения фактор-множества следует, что оно является подмножеством булеана: .Целые числа по модулю m
Напомним. Алгебра <М, , +>, которая по умножению является мультипликативным группоидом, по сложению — абелевой группой, причем умножение… Возьмем целое число m>1. Зададим отношение эквивалентности на множестве… ba b - a = m q для некоторого .Конгруэнции
Пример. Для двухместной операции сложения это выглядит так: для любых x и y из…Контрольные вопросы
Лекция № 7
Для математиков XIX в., занимавшихся алгеброй логики, наиболее важной проблемой было развитие технических приемов оперирования с элементарными утверждениями булевой алгебры, подобных тем, которые имеются в элементарной алгебре.
Х. Карри. Основания математической логики. М.: Мир,- 1969, стр. 420
ЭЛЕМЕНТЫ ТЕОРИИ ГРАФОВ
Теория графов применяется в таких областях, как физика, химия, теория связи, проектирование ЭВМ, электротехника, машиностроение, архитектура,… Эта теория тесно связана также со многими разделами математики, среди которых… Единого общепринятого определения графа нет. В зависимости от решаемой задачи принимается то или иное определение,…Определение.
 Неориентированным графом G называется множество N = {x,y,..} вместе с множеством A = {(x,y),..}(некоторых неупорядоченных пар), где множество N конечно (т.е. число его элементов конечно), а во множестве A нет элементов вида (х,х). Элементы множества N называют вершинами или узлами, элементы множества A называют ребрами. Обозначение неориентированного графа: G=(N,A)
Неориентированным графом G называется множество N = {x,y,..} вместе с множеством A = {(x,y),..}(некоторых неупорядоченных пар), где множество N конечно (т.е. число его элементов конечно), а во множестве A нет элементов вида (х,х). Элементы множества N называют вершинами или узлами, элементы множества A называют ребрами. Обозначение неориентированного графа: G=(N,A)
N = {x,y,s,z} - множество вершин неориентированного графа G.
A = {(sx),(sy),(xz),(xy),(yz)} - множество ребер неориентированного графа G
Граф, вершина, ребро
. Ориентированным графом (орграфом) будем называть такую произвольную пару G =… Граф G задается множеством точек или вершин х1,х2, . . ., хn ,которое обозначается через X, и множеством линий или…Дуга, ориентированный граф

Если ребра из множества Аориентированы, что обычно показывается стрелкой, то они называются дугами, и граф с такими ребрами называется ориентированным графом
Пример. (рис. (а)).
Соответствие
Для графа на рис. (а) имеем , т. е. вершины х2 и х5 являются конечными вершинами дуг, у которых начальной вершиной является х1 , ,Неориентированный граф
Пример. (рис. б) Ориентированным графом или орграфом называется множество N = {x,y,..} вместе с… В отличие от графа у орграфа пары (x,y) упорядочены.Инцидентность, смешанный граф
Направление предполагается заданным от первой вершины ко второй, когда дуга обозначается упорядоченной парой, состоящей из начальной и конечной…Эквивалентный ориентированный граф
 В случае неориентированного графа или графа, содержащего и дуги, и неориентированные ребра, предполагается, что соответствие Г задает такой эквивалентный ориентированный граф, который получаетсяиз исходного графа заменой каждого неориентированного ребра двумя противоположно направленными дугами, соединяющими те же самые вершины.
В случае неориентированного графа или графа, содержащего и дуги, и неориентированные ребра, предполагается, что соответствие Г задает такой эквивалентный ориентированный граф, который получаетсяиз исходного графа заменой каждого неориентированного ребра двумя противоположно направленными дугами, соединяющими те же самые вершины.
Пример 1. (см., графы, изображенные на рис. (б) и (в))
Пример 2.
Так, например, для графа, приведенного на рис. (б), имеем
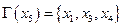 ,
,
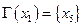 и т. д.
и т. д.
Обратное соответствие
и т. д. Для неориентированного графа для всех .Изоморфизм графов
е1 = (u,v) E1 е2 = (φ (u), φ (v)) E2 Теорема. Изоморфизм графов есть отношение эквивалентности. Графы G = <V, E>, G'= <V',E'> изоморфны, если существует такое взаимно однозначное отображение f из V на…Путь, ориентированный маршрут
Пример. На рис. 2 последовательности дуг а6, a5, a9, a8, a4 (1.1) a1, a6, a5, a9 (1.2)Смежные дуги, смежные вершины, степень вершины
Если вершины x и y неориентированного графа G соединены ребром (x,y), то вершины называются смежными, в противном случае - несмежные. Для неориентированного графа G: вершины, смежные вершине s - это x и y;… Степень вершины определим как число ребер, инцидентных ей. Вершину нулевой степени будем называть изолированной…Компонентная связность
Пусть G = <V, E> —произвольный неориентированный граф, и пусть 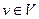 . Пусть А — множество тех вершин
. Пусть А — множество тех вершин  , к которым существует путь из v. Множество А вместе с ребрами графа G, инцидентными вершинам из А, определяет некоторый подграф, называемый компонентой связности графа G. Очевидно, что множества вершин компонент связности произвольного графа попарно не пересекаются.
, к которым существует путь из v. Множество А вместе с ребрами графа G, инцидентными вершинам из А, определяет некоторый подграф, называемый компонентой связности графа G. Очевидно, что множества вершин компонент связности произвольного графа попарно не пересекаются.
Ориентированная цепь
Если граф имеет цикл (необязательно простой), содержащий все рёбра графа по одному разу, то такой цикл называется эйлеровым циклом, а граф называется эйлеровым графом.
Ориентированной цепью (простой путь) (или, короче орцепью) называется такой путь, в котором каждая дуга используется не больше одного раза.
Пример.
Пути (а6, a5, a9, a8, a4) и (a1, a6, a5, a9) являются орцепями, а путь (a1, a6, a5, a9, a10, a6, a4) не является таким, поскольку дуга a6 в нем используется дважды.
Простая орцепь
IIростой орцепью (элементарный путь) называется такой путь, в котором каждая вершина используется не более одного раза.
Пример.
Путь (a1, a6, a5, a9) является простой орцепью, а пути (а6, a5, a9, a8, a4 1.1) и (1.3) — нет.
Простая орцепь является также орцепью, но обратное утверждение неверно.
Пример 1. Путь (1.1) является орцепью, но не простой орцепью.
Пример 2. Путь (a1, a6, a5, a9) является орцепью и простой орцепью.
Пример 3. Путь (1.3) не является ни орцепью, ни простой орцепью.
Цепи, простые цепи
Точно так же, как были определены орцепи и простые орцепи, можно определить цепи (простой маршрут) и простые цепи (элементарный маршрут).
Пример.
Маршрут (1.4) есть цепь и простая цепь, маршрут (1.5) — цепь, но не простая цепь, а маршрут (1.6) не является ни цепью, ни простой цепью.
Путь или маршрут можно изображать также последовательностью вершин.
Пример.
Путь (1.1) можно представить последовательностью вершин х2, х5, х4, х3, х5, х6 и такое представление часто оказывается более полезным в тех случаях, когда осуществляется поиск простых орцепей или простых цепей.
Вес, стоимость
Иногда дугам графа G сопоставляются (приписываются) числа — дуге (хi, хj) ставится в соответствие некоторое число cij называемое весом, или длиной, или стоимостью (ценой) дуги.
Связность
Теорема. Граф связен тогда и только тогда, когда его нельзя представить в виде…Граф со взвешенными дугами
Тем самым в взвешенном графе G каждой дуги xA поставлено в соответствие некоторое действительное число l(x). Значение l(x) называются длиной дуги… Для любого пути Pi взвешенного графа G обозначающим через l(Pi) сумму длин… В мультиграфе не допускаются петли, но пары вершин могут соединяться более чем одним ребром: эти ребра называют…3.
Матрица смежности: строки и столбцы соответствуют варшинам. Элемент матрицы
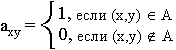
Пример. Составить матрицу смежности для графа G:
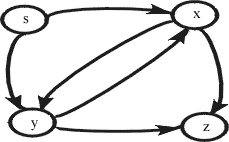
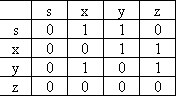
Заполняем строчку s: если есть дуга из s в другую вершину графа G, то ставим 1, если нет - 0. Из s есть дуги в x:(sx) и в y:(sy). По аналогии заполняем другие строки.
Матрица инцедентности: строки соответствуют вершинам, а столбцы дугам, при этом в столбце, соответствующем дуге (x,y) 1 ставится в строке x, -1 в строке y, остальные элементы равны 0.
Рисунок 3.1.13.

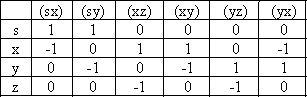
4.
Определение. Цепью длины n 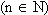 на графе (N,A) называется последовательность дуг
на графе (N,A) называется последовательность дуг  такая, что у любой дуги
такая, что у любой дуги 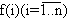 одна вершина общая с дугой f(i-1), а другая - общая с дугой f(i+1).
одна вершина общая с дугой f(i-1), а другая - общая с дугой f(i+1).
Вершина дуги f(1), не являющаяся общей с дугой f(2), называется началом цепи, вершина дуги f(n), не являющаяся общей с дугой f(n-1), называется концом цепи.
Если начало цепи совпадает с ее концом, то цепь называется циклом.
Определение. Путем длины n 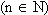 на графе (N,A) называется последовательность дуг
на графе (N,A) называется последовательность дуг  такая, что у любой дуги f:(i)(i=1..n) начала дуги совпадает с концом дуги f(i-1), а конец дуги совпадает с началом дуги f(i+1).
такая, что у любой дуги f:(i)(i=1..n) начала дуги совпадает с концом дуги f(i-1), а конец дуги совпадает с началом дуги f(i+1).
Начало дуги f(1) называется началом пути, конец дуги f(n) называется концом пути.
Если начало пути совпадает с концом пути, то путь называют контуром.
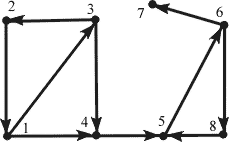
Из 2 в 7 путь длины 6:(2,1),(1,3),(3,4),(4,5),(5,6),(6,7).(Двигается по направлению стрелок). Контур длины 3:(2,1),(1,3),(3,2).
Из 2 в 8 цепь длины 4:(2,3),(3,4),(4,5),(5,8). Цикл длины 4:(2,1),(1,4),(4,3),(3,2).
Определение. Граф называется связным, если для любых двух его вершин x и y существует цепь, соединяющая x и y.
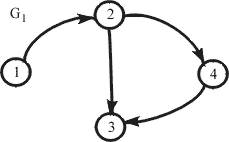

Определение. Говорят, что вершина у графа G достижима из вершины x, если существует путь из x в y.

вершина 2 достижима из 1:(1,2)
вершина 4 достижима из 1:(1,2),(2,4)
вершина 3 не достижима из 1.
Определение. Граф называется сильно связным, если для любых двух его вершин x и y, существует путь соединяющий x и y.

Определение. Компонентой сильной связности графа G называется его сильно связный подграф, не являющийся подграфом никакого другого сильно связного подграфа G.
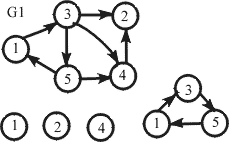
Получили 4 компоненты сильной связности графа G1 (вершина является компонентой сильной связности).

Рисунок 3.1.22.
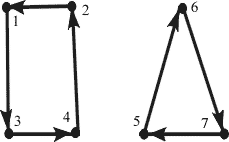
Получим 2 компоненты сильной связности графа G2.
Определение. Пусть дан граф G=(N,A)(N=[V1,...,Vn]). Матрицей достижимости графа G называется квадратная матрица 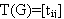 порядка n, у которой
порядка n, у которой  , если вершина Vj достижима из Vi, и
, если вершина Vj достижима из Vi, и 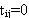 - в противоположном случае.
- в противоположном случае.
Определение. Матрицей сильной связности графа G=(N,A) называется матрица  порядка n, у которой
порядка n, у которой 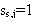 , если вершина Vj достижима из Vi, и
, если вершина Vj достижима из Vi, и  - в противоположном случае.
- в противоположном случае.

Матрица достижимости.
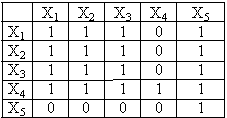
Матрица достижимости: по диагонали ставим 1 (считается что вершина достижима сама из себя); заполняем строку X1 - если вершина достижима из X1 то в соответствующем этой вершине столбце ставим 1, в противном случае 0; по аналогии заполняем остальные строки.
Матрица сильной связности.
Матрица сильной связности: по диагонали ставим 1; заполняем строку X1 - если вершина достижима из X1 и X1 достижима из этой вершины, то в… Замечание. По матрице сильной связности можно выписать компоненты сильной… Выпишем компоненты сильной связности для рассмотренного графа.Пример 1.
G1
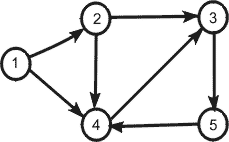
G2

G1UG2
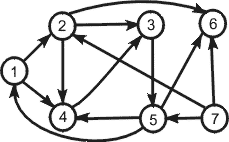
Определение. Пересечением графов 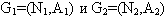 граф, у которого пересечены множество вершин и множество дуг графов
граф, у которого пересечены множество вершин и множество дуг графов 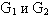 . Обозначение
. Обозначение  .
.
Пример 2. Рассмотрим графы 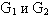 из примера 1. Построим их пересечение: выберем одинаковые вершины и дуги.
из примера 1. Построим их пересечение: выберем одинаковые вершины и дуги.
Подграф
Подграфом графа G = <V, E> будем называть такой произвольный граф G'= <V',E'>, что 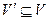 и
и 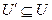 . В отечественной литературе по теории графов граф G' называется чаще частью графа, или частичным графом, под подграфом же понимается частичный граф, удовлетворяющий дополнительному условию
. В отечественной литературе по теории графов граф G' называется чаще частью графа, или частичным графом, под подграфом же понимается частичный граф, удовлетворяющий дополнительному условию 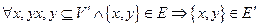 .
.
Контрольные вопросы и задачи
Лекция № 8
Когда вы убедитесь, что теорема верна, вы начинаете ее доказывать.
Традиционный профессор математики. А. Пойа Математика и правдоподобные рассуждения. М.: Наука, 1975 стр. 97
ДЕРЕВЬЯ
Одним из простейших классом графов являются деревья. Граф является деревом, если он удовлетворяет следующей теореме. Теорема. Для графа G= <X,U> следующие утверждения эквивалентны: 1) G - дерево;Свободные деревья
Граф без циклов называется ациклическим, или лесом. Связный ациклический граф называется (свободным) деревом. Компонентами связности леса являются деревья.
Граф G, в котором q(G) = р(G)-1, называется древовидным.
В ациклическом графе G z(G) = 0. Пусть и, v — несмежные вершины графа G, х = (и,v)  E. Если граф G+x имеет только один простой цикл, z(G+х)= 1, то граф G называется субциклическим.
E. Если граф G+x имеет только один простой цикл, z(G+х)= 1, то граф G называется субциклическим.
Пример
На рис. 9.1 показаны диаграммы всех различных (свободных) деревьев с 5 вершинами, а на рис. 9.2 — диаграммы всех различных (свободных) деревьев с 6 вершинами.

Рис. 8.1. Свободные деревья с 5 вершинами

|


Рис. 8.2. Свободные деревья с 6 вершинами
Основные свойства деревьев
Следующая теорема устанавливает, что два из четырех свойств — связность, ацикличность, древовидность и субцикличность — характеризуют граф как дерево.
Теорема
Пусть G(V, Е) — граф с р вершинами, q ребрами, k компонентами связности и z простыми циклами. Пусть далее х — ребро, соединяющее любую пару несмежных вершин в G. Тогда следующие утверждения эквивалентны:
1. G — дерево, то есть связный граф без циклов, k(G) = 1&z(G) = 0;
2. любые две вершины соединены в G единственной простой цепью,
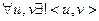 .
.
3. G — связный граф, и любое ребро есть мост,
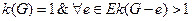 ;
;
4. G — связный и древовидный,
 ;
;
6. G — ациклический и субциклический,
 ;
;
7. G — связный, субциклический и неполный,
 ;
;
8. G — древовидный и субциклический (за двумя исключениями),
 ;
;
Доказательство
Рис. 8.3. К доказательству теоремы о свойствах деревьев
[1 2] От противного. Пусть существуют две цепи <и, v> (рис. 9.3, слева). Тогда w, w2 — простой цикл.
2] От противного. Пусть существуют две цепи <и, v> (рис. 9.3, слева). Тогда w, w2 — простой цикл.

|
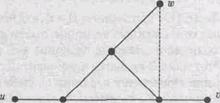
|
[2 3.] Имеем:
3.] Имеем:  и, v
и, v  !, следовательно,
!, следовательно, 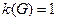 . Далее от противного. Пусть ребро х — не мост. Тогда в G - х концы этого ребра связаны цепью. Само ребро х — вторая цепь.
. Далее от противного. Пусть ребро х — не мост. Тогда в G - х концы этого ребра связаны цепью. Само ребро х — вторая цепь.
[3 4.] Индукция по р. База: р = 1
4.] Индукция по р. База: р = 1  q = 0. Пусть
q = 0. Пусть  для всех связанных графов G с числом вершин меньше р, у которых любое ребро суть мост. Тогда удалим из G ребро х (которое является мостом). Получим две компоненты G' и G", удовлетворяющие индукционному предположению. Имеем:
для всех связанных графов G с числом вершин меньше р, у которых любое ребро суть мост. Тогда удалим из G ребро х (которое является мостом). Получим две компоненты G' и G", удовлетворяющие индукционному предположению. Имеем:
 .
.
[4 5.] От противного. Пусть есть цикл с п вершинами и п ребрами. Остальные р - п вершин имеют инцидентные им рёбра, которые связывают их с циклом, Следовательно, q ≥ р, что противоречит условию q = р - 1.
5.] От противного. Пусть есть цикл с п вершинами и п ребрами. Остальные р - п вершин имеют инцидентные им рёбра, которые связывают их с циклом, Следовательно, q ≥ р, что противоречит условию q = р - 1.
[5 1.] Граф без циклов, следовательно, его компоненты — деревья. Пусть их k;. Имеем:
1.] Граф без циклов, следовательно, его компоненты — деревья. Пусть их k;. Имеем:
 i = У(pi-1) = Уpi-k = p-k
i = У(pi-1) = Уpi-k = p-k
Но q=p-1, следовательно, k = 1.
[5 6.] По ранее доказанному 5
6.] По ранее доказанному 5  1
1  2. Имеем:
2. Имеем: 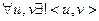 . Соединив две несмежные вершины, получим единственный простой цикл.
. Соединив две несмежные вершины, получим единственный простой цикл.
[6 7.] При р ≥ 3 граф Кр содержит цикл, следовательно, G ≠ Кр. Далее от противного. Пусть G несвязен, тогда при соединении ребром двух компонент связности цикл не возникнет.
7.] При р ≥ 3 граф Кр содержит цикл, следовательно, G ≠ Кр. Далее от противного. Пусть G несвязен, тогда при соединении ребром двух компонент связности цикл не возникнет.
[7 2.] Имеем k(G) = 1, следовательно,
2.] Имеем k(G) = 1, следовательно, 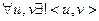 . Пусть цепь не единственная. Тогда существует цикл Z, причем Z = К3, = С3. Действительно, пусть Z > С3, тогда, соединив две несмежные вершины этого цикла, получим два цикла. Но G связен и G ≠ К3, следовательно, существует другая вершина w, смежная с Z = К3 (см. рис. 9.3, справа). Если w смежна более чем с одной вершиной Z, то имеем больше одного цикла. Если w смежна только с одной вершиной Z, то соединив её с другой вершиной, получим два цикла.
. Пусть цепь не единственная. Тогда существует цикл Z, причем Z = К3, = С3. Действительно, пусть Z > С3, тогда, соединив две несмежные вершины этого цикла, получим два цикла. Но G связен и G ≠ К3, следовательно, существует другая вершина w, смежная с Z = К3 (см. рис. 9.3, справа). Если w смежна более чем с одной вершиной Z, то имеем больше одного цикла. Если w смежна только с одной вершиной Z, то соединив её с другой вершиной, получим два цикла.
[7 8.] Имеем k(G) = 1, следовательно, G ≠ К2
8.] Имеем k(G) = 1, следовательно, G ≠ К2 К3, G ≠ К1
К3, G ≠ К1 К3. Имеем по доказанному: 7
К3. Имеем по доказанному: 7  2
2  3
3  4, то есть q = р- 1.
4, то есть q = р- 1.
[8 5.] От противного. Пусть в G есть цикл Z = Сп. Если n > 3, то если внутри Z уже есть смежные вершины, имеем два цикла. Если в Z нет смежных вершин, то, соединив несмежные вершины в Z, получим два цикла. Следовательно, Z = К3. Этот цикл Z является компонентой связности G. Действительно, пусть это не так. Тогда существует вершина w, смежная с Z. Если w смежна более чем с одной вершиной Z, то имеем больше одного цикла. Если w смежна только с одной вершиной Z, то, соединив её с другой вершиной, получим два цикла. Рассмотрим G :=G - Z. Имеем: р = р' + 3, q = q' + 3. Но q = р - 1, следовательно, q' = р' - 1. Отсюда z(С') = 0, так как один цикл уже есть. Следовательно, компоненты G' — деревья. Пусть их k. Имеем:
5.] От противного. Пусть в G есть цикл Z = Сп. Если n > 3, то если внутри Z уже есть смежные вершины, имеем два цикла. Если в Z нет смежных вершин, то, соединив несмежные вершины в Z, получим два цикла. Следовательно, Z = К3. Этот цикл Z является компонентой связности G. Действительно, пусть это не так. Тогда существует вершина w, смежная с Z. Если w смежна более чем с одной вершиной Z, то имеем больше одного цикла. Если w смежна только с одной вершиной Z, то, соединив её с другой вершиной, получим два цикла. Рассмотрим G :=G - Z. Имеем: р = р' + 3, q = q' + 3. Но q = р - 1, следовательно, q' = р' - 1. Отсюда z(С') = 0, так как один цикл уже есть. Следовательно, компоненты G' — деревья. Пусть их k. Имеем:
 I = У(pi-1) = Уpi-k = ṕ-k
I = У(pi-1) = Уpi-k = ṕ-k
но q' = p' -1, следовательно. k = 1. то есть дерево одно. Если в этом дереве сбединить несмежные вершины, то получим второй цикл. Два исключения: деревья, которые не имеют несмежных вершин, — это К1 и K2.
Общая схема доказательства представлена на рис. 9.4. Граф доказательства сильно связен, следовательно, теорема доказана.
Вычисление
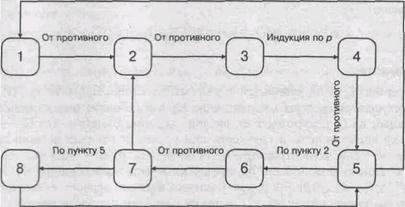
Рис. 9.4. Схема доказательства теоремы о свойствах деревьев
От противного
Следствие 1 В любом нетривиальном дереве имеются по крайней мере две висячие вершины.
Рассмотрим дерево G(V, Е). Дерево — связный граф, следовательно, . Далее от противного. Пусть . Тогда 2q = Уd(vi) > 2(р - 1) + 1 = 2р - 1.Центр дерева
Свободные деревья выделяются из других графов тем, что их центр всегда оправдывает своё название.
Теорема
Z(G) = 0&k(G) = 1 → С(G) = К1 С(G) = К2. Доказательство Для деревьев К1 и К2 утверждение теоремы очевидно. Пусть теперь G(V,Е) — некоторое свободное дерево, отличное от К1 и…Ориентированные, упорядоченные и бинарные деревья
Ориентированным деревом (или ордеревом, или корневым деревом)называется орграф со следующими свойствами. 1. Существует единственный узел r, полустепень захода которого равна 0, d+(r)… 2. Полустепень захода всех остальных узлов равна 1, v V {r } d+(r) = 1 == 1.Пример
На рис. 9.5 приведены диаграммы всех различных ориентированных деревьев с 3 узлами, а на рис. 9.6 показаны диаграммы всех различных ориентированных деревьев с 4 узлами.
Теорема. Ордерево обладает следующими свойствами:
1. q = р - 1;
2. если в ордереве забыть ориентацию дуг, то получится свободное дерево;
3. в ордереве нет контуров
4. для каждого узла существует единственный путь, ведущий в этот узел из корня;
5. подграф, определяемый множеством узлов, достижимых из узла v, является ордеревом с корнем v (это ордерево называется поддеревом узла v);
6. если в свободном дереве любую вершину назначить корнем, то получится ордерево.

рис. 9.5. Ориентированные деревья с 3 узлами
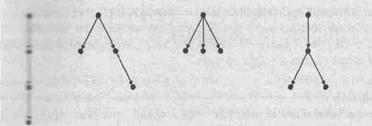
Рис. 9.6. Ориентированные деревья с 4 узлами
Доказательство
v V {r } d+(r) = 1, где r — корень. Следовательно, q = р - 1. 2. Пусть G — ордерево, граф G' получен из G забыванием ориентации рёбер, r —… 3. Следует из пункта 2.Т ≡ {{r}, Т1,.. ., Тk}.
Нетрудно видеть, что данное определение эквивалентно определению 9.2.1. Достаточно построить орграф, проводя дуги от заданного узла r к корням поддеревьев Т1,.. ., Тk и далее повторяя рекурсивно этот процесс для каждого из поддеревьев.
Упорядоченные деревья
Пример Ориентированные и упорядоченные ориентированные деревья интенсивно… 1. Выражения. Для представления выражений языков программирования, как правило, используются ориентированные…Рис. 9.8. Диаграммы деревьев
Бинарные деревья
Бинарное дерево не является упорядоченным ордеревом. Пример На рис. 9.9 приведены две диаграммы деревьев, которые изоморфны как упорядоченные, ориентированные и свободные…Представление деревьев в компьютере
Обсуждению представлений деревьев можно предпослать в точности те же рассуждения, что были предпосланы обсуждению представлений графов (см. 7.4). Кроме того, следует подчеркнуть, что задача представления деревьев в программе встречается гораздо чаще, чем задача представления графов общего вида, а потому методы ее решения оказывают еще большее влияние на практику программирования.
Представление свободных деревьев
Рассмотрим следующее представление свободного дерева, известное как код Прюфера. Допустим, что вершины дерева T(V, Е) занумерованы числами из… Алгоритм 9.1. Построения кода Прюфера свободного дерева Вход: Дерево T(V,Е) в любом представлении, вершины дерева занумерованы числами 1 ... р произвольным образом.For: from 1 to p – 1 do
v: = тin {k  V|d(k) = 1} { выбираем вершину v — висячую вершину с наименьшим номером }
V|d(k) = 1} { выбираем вершину v — висячую вершину с наименьшим номером }
А[i]: = Г(v) { заносим в код номер единственной вершины, смежной с v}
V: = V — v { удаляем вершину v из дерева }
End for
По построенному коду можно восстановить исходное дерево с помощью алгоритма 9.2.
Алгоритм 9.2. Распаковки кода Прюфера свободного дерева
Вход: Массив А:Массив А: аrrау [1...р- 1] оf 1..р — код Прюфера дерева Т.
Выход: Дерево T(V,Е), заданное множеством рёбер Е, вершины дерева занумерованы числами 1...р.
Е: =  { в начале множество рёбер пусто}
{ в начале множество рёбер пусто}
В:= 1...р { множество неиспользованных номеров вершин }
For: from 1 to p – 1 do
v: = тin {k  В |
В | j ≥ i k ≠ A[j]} { выбираем вершину v; — неиспользованную вершину с наименьшим номером, который не встречается в остатке кода Прюфера }
j ≥ i k ≠ A[j]} { выбираем вершину v; — неиспользованную вершину с наименьшим номером, который не встречается в остатке кода Прюфера }
Е: = Е + (v, А[i]) {добавляем ребро (v, А[i]) }
В :=В - v { удаляем вершину v из списка неиспользованных}
End for
Обоснование Код Прюфера действительно является представлением свободного дерева. Чтобы… Для этого установим отображение f: 1..р → 1..р между номерами вершин в деревьях Т, и Т' по порядку выбора вершин…Пример
Для дерева, представленного на рис. 9.10, код Прюфера 7, 9, 1, 7, 2, 2, 7, 1, 2, 5, 12. На этом рисунке числа в вершинах - это их номера, а числа на рёбрах указывают порядок, в котором будут выбираться висячие вершины и удаляться рёбра при построении кода Прюфера.
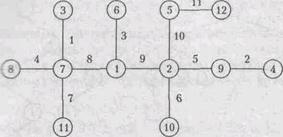
Рис. 9.10. Построение кода Прюфера
Замечание
Код Прюфера — наиболее экономное по памяти представление дерева. Его можно немного улучшить, если заметить, что существует всего одно дерево с двумя вершинами — К2, а потому информацию о «последнем ребре» можно не хранить, она восстанавливается однозначно.
Представление бинарных деревьев
Пример На рис. 9.11 приведены диаграммы упорядоченного и соответствующего ему бинарного деревьев.Контрольные вопросы
1. Что называется графом? Ориентированным графом? Примеры.
2. Что такое степень вершины?
3. Перечислите основные понятия, связанные с неориентированными графами.
4. Перечислите основные понятия, связанные с ориентированными графами.
5. Перечислите способы задания графов.
6. В чем состоит аналитический способ задания графа?
7. В чем состоит геометрический способ задания графа?
8. В чем состоит матричный способ задания графа?
9. Какая матрица называется матрицей смежности графа?
10. Какая матрица называется матрицей смежности графа?
11. Какая матрица называется матрицей инцидентности графа?
12. Что называется маршрутом, циклом и цепью графа?
13. Сформулируйте понятие связности графа. Какой граф называется связным?
14. Какие два графа называются изоморфными?
15. Сформулируйте алгоритм изоморфизма двух графов.
16. Перечислите операции над графами.
17. Дайте определение эйлерова графа.
18. Сформулируйте алгоритм построения эйлерова цикла.
19. Какой граф называется гамильтоновым?
Лекция № 9
БУЛЕВА АЛГЕБРА
Так как здание всего мира совершенно и возведено премудрым Творцом, то в мире не происходит ничего, в чем не было бы виден смысл какого-нибудь максимума или минимума.
Эйлер
Булевой алгеброй называется дистрибутивная структура с неравными друг другу единицей 1 и нулем 0, в которой всякий элемент имеет дополнение. Булева алгебра всегда содержит не менее двух элементов. Алгебра, содержащая только 1 и 0, называется вырожденной.
Основные логические функции
Декартово произведение E Е Е … E = En является множеством упорядоченных наборов, состоящих из п чисел (нулей и единиц). Как известно, Еп cодержит 2п… Например, при п = 3 множество Е3 может быть упорядочено следующим образом. … Такое упорядочение еще называют “скользящей единицей”.Булева функция.
Функции алгебры логики (ФАЛ) называются также булевыми функциями, двоичными функциями и переключательными функциями. Булевой функцией описываются преобразования некоторым устройством входных… Иначе говоря, булева функция – это функция, и аргументы и значение которой принадлежит множеству {0, 1}. Множество {0,…Двухэлементная булева алгебра.
Тогда система Bо = является двухэлементной булевой алгеброй со всеми свойствами на операции. Формулы алгебры логики, содержащие лишь логические… По теореме о функциональной полноте в булевой алгебре Bо с помощью терма можно…Таблицы булевых функций
При n = 1 имеем 4 булевых функции x f1(x) f2(x) f3(x) f4(x) … f1(x) - тождественная функция f2(x) - константа 0F3 – повторение по x
f4 – запрет по x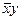
F5 – повторение по y
f7 – дизъюнкция f8 – стрелка Пирса f9 – эквивалентностьПорядок выполнения операций
Соглашения относительно расстановки скобок. 1. Внешние скобки не пишутся. Пример. Вместо пишутЭквивалентность формул
Формулы φ(x1,..., xn) и ψ(x1,..., xn) называются эквивалентными (φ ~ ψ), если совпадают их таблицы истинности, т. е. совпадают… Пример 1. Проверка на эквивалентность следующих формул и . Построим таблицы… убеждаемся в том, что ~ . Действительно это отношение ~ является отношением эквивалентности, т. е. оно рефлексивно…Замечание
2. Формула φ опровержима тогда и только тогда, когда она не является тождественно истинной (|φ); 3. Формула φ выполнима тогда и только тогда, когда она не является… Тождественно истинные (соответственно тождественно ложные) формулы образуют класс эквивалентности по отношению ~.Графический способ задания булевой функции
Единичный n-мерный куб функции w = f(x, y, z)
Задняя 001 011 Задняя 101 111
Грань передняя
000 001 100 110
Фактор-алгебра алгебры формул
На множестве Фn определены двухместные операции конъюнкции и дизъюнкции — : , : — и одноместная операция отрицания : . Выделим на множестве Фn две константы и . Так получается алгебра формул Fn =… Отношение ~ эквивалентности формул является конгруэнцией на алгебре Fn, и поэтому можно задать фактор-алгебру Fn/~. …ДИЗЪЮНКТИВНЫЕ И КОНЪЮНКТИВНЫЕ НОРМАЛЬНЫЕ ФОРМЫ
Определение
называется литерой. Литеры х и называются контрарными. Элементарной конъюнкцией или конъюнктом называется конъюнкция литер.Алгоритм приведения формулы к ДНФ.
~ ~ и определения операций:Совершенные ДНФ (СДНФ) и КНФ (СКНФ).
Конституентой единицы набора Δ называется конъюнкт K1(δ1 ... δп) = . Конституентой нуля набора Δ называется дизъюнкт K0(δ1 … δп) =… Отметим, что K1(δ1 ... δп) = 1, а K0(δ1 … δп) = 0 тогда и только тогда, когда х1 = δ1, х2 =…Первая теорема Шеннона
Теорема (первая теорема Шеннона). Любая булева функция f(x1, х2,...,xп) представима в виде разложения Шеннона: Доказательство. Прежде всего, заметим, что . Подставим произвольно вместо первых k переменных их значения: . Тогда…Вторая теорема Шеннона
Теорема 6.4.3 (вторая теорема Шеннона). Любая булева функция f(x1, х2,...,xп) представима в виде разложения Шеннона: В предельном случае, когда k = n, для булевой функции f(x1, х2,...,xп), не равной нулю, получаем ее представление в…Функциональная полнота
и такое представление единственно с точностью до порядка следования… ,Алгоритм нахождения СДНФ.
а) если в конъюнкт входит некоторая переменная вместе со своим отрицанием, то нужно удалить этот конъюнкт из ДНФ; б) если в конъюнкт одна и та же литера хδ входит несколько раз, то… в) если в некоторый конъюнкт не входит переменная y, то этот конъюнкт заменить на эквивалентную формулу применяя закон…Минимизация булевых функций в классе ДНФ
Вхождение переменной – это место, которое переменная занимает в формуле. Каждая формула имеет конечное число вхождений переменных. Задача заключается в том, чтобы для данной булевой функции f найти ДНФ, представляющую эту функцию и имеющую наименьшее число вхождений переменных.
Элементарным произведением называется конъюнкт, в который любая переменная входит не более одного раза.
Пример 6.6.1. Формула  — элементарное произведение, а формула
— элементарное произведение, а формула  элементарным произведением не является.
элементарным произведением не является.
Формула φ(x1, x2,…,xп) называется импликантой формулы ψ(x1, x2,…,xп), если φ — элементарное произведение и φ ψ ~ φ, т. е. для соответствующих формулам φ и ψ функций fφ и fψ справедливо неравенство fφ ≤ fψ. Формула φ(x1, x2,…,xп) называется импликантой функции f, если φ — импликанта совершенной ДНФ, представляющей функцию f.
ψ ~ φ, т. е. для соответствующих формулам φ и ψ функций fφ и fψ справедливо неравенство fφ ≤ fψ. Формула φ(x1, x2,…,xп) называется импликантой функции f, если φ — импликанта совершенной ДНФ, представляющей функцию f.
Импликанта φ(x1, x2,…,xп)= 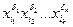 формулы ψ называется простой, если после отбрасывания любой литеры из φ не получается формула, являющаяся импликантой формулы ψ.
формулы ψ называется простой, если после отбрасывания любой литеры из φ не получается формула, являющаяся импликантой формулы ψ.
Пример 6.6.2. Найти все импликанты и простые импликанты для формулы
φ (х,у) = х → у.
Всего имеется 8 элементарных произведений с переменными х и у. Ниже приведены их таблицы истинности:
| x | y | φ = x →y | 
| 
| 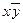
| 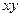
| 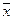
| 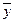
| x | y |
Из таблиц истинности заключаем, что формулы  ,
,  , ху,
, ху, 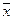 , у — все импликанты формулы φ, а из этих импликант простыми являются формулы
, у — все импликанты формулы φ, а из этих импликант простыми являются формулы 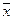 и у. Hапример, формула
и у. Hапример, формула  ,не является простой импликантой, поскольку отбрасывая литеру
,не является простой импликантой, поскольку отбрасывая литеру 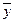 , получаем импликанту
, получаем импликанту 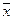 .
.
Дизъюнкция всех простых импликант данной формулы (функции) называется сокращенной ДНФ.
Теорема. Любая булева функция, не являющаяся константой 0, представима в виде сокращенной ДНФ.
В примере функция, соответствующая формуле x→y, представима формулой  , которая является ее сокращенной ДНФ.
, которая является ее сокращенной ДНФ.
Сокращенная ДНФ может содержать лишние импликанты, удаление которых не меняет таблицы истинности. Если из сокращенной ДНФ удалить все лишние импликанты, то получается ДНФ, называемая тупиковой. Представление функции в виде тупиковой ДНФ в общем случае неоднозначно.
Выбор из всех тупиковых форм формы с наименьшим числом вхождений переменных дает минимальную ДНФ (МДНФ).
Метод Квайна
- операция полного склеивания - ~ ~ φ; - операция неполного склеивания - ~ ~ ; - операция элементарного поглощения - ~ φ, .ПОЛНЫЕ СИСТЕМЫ БУЛЕВЫХ ФУНКЦИЙ
Каноническое представление логических функций
В алгебре логики каноническими формами логических функций является совершенная конъюнктивная нормальная форма (СКНФ) и совершенная дизъюнктивная… 1. СДНФ (совершенной ДНФ) называется ДНФ, в которой нет равных элементарных… В этой формуле присутствуют элементарные конъюнкции второго ряда (в ВТ называемые минтермами).Системы булевых функций
f(и g1(x1, x2, …, xn,), g2(x1, x2, …, xn,), …, gm(x1, x2, …, xn,)), которую называют суперпозицией функций f и gi (i = 1,2,…m), т.е. при помощи… Набор булевых функций M = { f1, f2, … ,fk} называется полной системой булевых функций или базисом, если любая булева…Базис Жегалкина.
Классы булевых функций
Множество всех булевых функций P2 является замкнутым классом (Почему?). Общее их число всех булевых функций n переменных равно его мощности 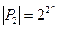 . Из множества этих функций выделяют некоторые классы (подмножества).
. Из множества этих функций выделяют некоторые классы (подмножества).
1. Булева функция f сохраняет константу 0, если
f(0, 0, … , 0) = 0
Множество всех булевых функций, сохраняющих константу 0, образует класс  .
.
Теорема. Число всех булевых функций, сохраняющих константу 0, равно 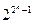 .
.
Доказательство. Булева функция, принадлежащая классу K0 , на наборе <0, 0, …, 0> принимает значение равное 0, но таких наборов 2n – 1, следовательно общее число таких функций 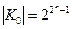 .
.
2. Булева функция f сохраняет константу 1, если
f(1, 1, … , 1) = 1
Множество всех булевых функций, сохраняющих константу 1, образует класс 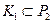 .
.
Теорема. Число всех булевых функций, сохраняющих константу 1, равно 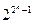 .
.
Доказательство. Булева функция, принадлежащая классу K1 , на наборе <1, 1, …, 1> принимает значение равное 1, но таких наборов 2n – 1, следовательно общее число таких функций 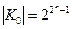 .
.
3. Булева функция 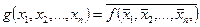 называется двойственной функцией к функции f и обозначается f*.
называется двойственной функцией к функции f и обозначается f*.
ZB. По определению 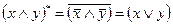 , т.е. функция
, т.е. функция 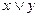 является двойственной к функции
является двойственной к функции 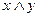 .
.
Рассмотреть, что происходит с таблицей истинности.
Замечание. Замена кортежей соответствует переворачиванию таблицы.
Булева функция называется самодвойственной, если она совпадает с двойственной себе функцией f = f*.
ZB. Класс самодвойственных булевых функций: 1.  ; 2.
; 2. 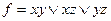 .
.
Множество всех самодвойственных булевых функций, образует класс  .
.
Теорема. Число всех самодвойственных булевых функций равно 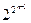 .
.
Доказательство. Любую булева самодвойственную функция, принадлежащая классу S , можно определить на половине наборов, т.е. 2n-1 , следовательно, общее число таких функций 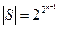 .
.
4. Булева функция f называется линейной функцией, если она может быть записана в следующем виде 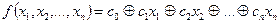 , где
, где  .
.
Множество всех линейных булевых функций, образует класс 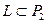 .
.
Теорема. Число всех линейных булевых функций равно 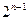 .
.
Доказательство. Имеется всего 2n+1 различных наборов значений коэффициентов ck. следовательно, общее число таких функций  .
.
5. Набор значений переменных  не меньше набора
не меньше набора  , если
, если 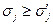 для всех j = 1, 2, …, n. В этом случае пишут
для всех j = 1, 2, …, n. В этом случае пишут 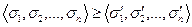 , в противном случае наборы называются несравнимыми.
, в противном случае наборы называются несравнимыми.
Булева функция f называется монотонной функцией, если для любых двух наборов, таких, что 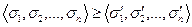 имеет место неравенство
имеет место неравенство
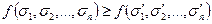 .
.
Множество всех монотонных булевых функций, образует класс  .
.
Число всех монотонных булевых функций оценивается асимптотически:
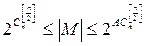 , где А – некоторая константа.
, где А – некоторая константа.
Теорема (Пост-Яблонского).
Для того чтобы множество N булевых функций было полной системой, необходимо и достаточно найти для каждого из пяти замкнутых классов Поста K0, K1, S, M, L функцию из N , которая ему не принадлежит.
ZB. Рассмотрим множество из одной функции Шеффера 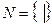 . Это - полная система. Согласно теореме Поста эта единственная функция должна не принадлежать ни одному из классов Поста.
. Это - полная система. Согласно теореме Поста эта единственная функция должна не принадлежать ни одному из классов Поста.
1. 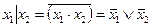 ;
;  вывод
вывод 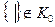
2. 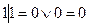 вывод
вывод 
3.  вывод
вывод 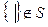
4.  вывод
вывод 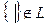
5.  вывод
вывод 
Теорема Поста
(Post E.L. The two-valued interactive systems of mathematical logic. – Annals of Math. Studies, v. 5, Princeton Univ. Press. Princeton-London,… Требования : P2 класс - замкнутый, то Базис - конечный. Теорема (Пост). Каждый замкнутый класс из P2 имеет конечный базис.Доказательство.
Введем обозначение: i – один из индексов 0, 1, *, ≤, L . Тогда , но по таблице Таблица принадлежности некоторых булевых функций рассмотренным замкнутым классам: …Алгебра Жегалкина
A = <FB, ,,0,1>ЛОГИКА ВЫСКАЗЫВАНИЙ
Известно, что в исчислении высказываний теоремами являются общезначимые формулы, поэтому автоматизация доказательства осуществляется в виде… ОпределенияA ~ с ≡ b ~ с; с ~ a ≡ с ~b.
Доказательство. Рассмотрим табличный метод перебора всех оценок формул. Надо для восьми (почему?) случаев оценок формул a, b, с
a = И, b = И, с = И;
а = И, b = И, с = Л;
и т. д.
А = Л; b = Л, с = Л
убедиться в правильности каждой равносильности.
Теорема 2 (правило равносильных замен переменных).
Пусть а = b и с — формула, в которой выделено одно вхождение переменной X. Пусть са получается из с заменой этого вхождения X на а, а сb из с заменой того же вхождения X на b. Тогда cа ≡ cb.
Доказательство. Эту теорему докажем методом математической индукции по числу п логических связок в формуле с.
Для п = 0 формула с = X (не имеет логических связок). Тогда са = а и сb = b. Следовательно, утверждение теоремы верно.
Пусть теорема верна для формулы с числом связок, не превосходящим натурального п > 0.
Рассмотрим случай, когда имеется п + 1 логическая связка. Тогда формула имеет один из пяти возможных видов с =  d, с = f
d, с = f g, с = f&g, с = (f => g), с = (f ~g). Здесь d, f, g — формулы с числом логических связок не более n, для которых теорема справедлива. Заметим, что са =
g, с = f&g, с = (f => g), с = (f ~g). Здесь d, f, g — формулы с числом логических связок не более n, для которых теорема справедлива. Заметим, что са = da, cb =
da, cb = db или са = fa
db или са = fa gа, сb = fb
gа, сb = fb  gb, или са = fa & ga, сb = fb
gb, или са = fa & ga, сb = fb  gb или и т. д. Так как для формул d, f, g теорема справедлива, имеем da≡db, fa≡fb, ga ≡gb. Тогда в силу предыдущей теоремы получим то, что требовалось доказать.
gb или и т. д. Так как для формул d, f, g теорема справедлива, имеем da≡db, fa≡fb, ga ≡gb. Тогда в силу предыдущей теоремы получим то, что требовалось доказать.
Определение 12. Подформулой формулы с называется любое подслово с, само являющееся формулой.
Следующие правила приведем без доказательств [Нефедов В.Н. Курс дискретной математика. – М.: Изд-во МАИ, 1992].
Теорема 3 (правило равносильных замен подформул).
Пусть са — формула, содержащая а в качестве своей подформулы. Пусть сb получается из са заменой а в этом вхождении на b. Тогда, если а ≡b, то са ≡cb,.
Теорема 4 (правило устранения импликаций и эквивалентностей).
Для каждой формулы можно указать равносильную ей формулу, не содержащую логических символов  и ~.
и ~.
Правило перехода к булевым функциям.
Нетрудно показать, что всякая формула логики высказываний может быть представлена булевой функцией и, наоборот, всякая булева функция соответствует некоторой формуле логики высказываний. Для этого достаточно перекодировать (переобозначить) логическое значение истинностной оценки языковых текстов следующим образом. Значение истина обозначить числом 1, а значение ложь числом 0. Далее, всякую атомарную формулу X, Y, ... логики высказываний, с помощью которой моделируем языковый текст, надо обозначить булевой переменной х, у, ... Теперь всякая оценка атомарной формулы будет соответствовать заданию значения булевой переменной. Всякая формула логики высказываний будет соответствовать своей булевой функции. При этом таблица истинности формулы будет соответствовать табличному заданию булевой функции, а аналитическое задание формулы аналитическому заданию булевой функции. Логические связки логики высказываний будут знаками алгебраических операций над булевыми переменными и константами.
Например, формула логики высказываний
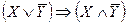
будет соответствовать булевой функции
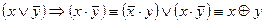 .
.
Здесь X, Y обозначено через х,у, знак конъюнкции & — через •, знак отрицания  X — через
X — через 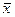 .
.
Рассмотрим текстовую логическую задачу.
Нормальные формы формул логики высказываний
Определим теперь нормальные формы формул. Сначала заметим, что, в силу ассоциативности операций & и  , как бы не расставляли скобки в выражениях:
, как бы не расставляли скобки в выражениях:
А1 & А2 & ... & Ак; A1  A2
A2 ...
... Ak (к > 3),
Ak (к > 3),
всегда будем приходить к равносильным формулам.
Определение 13. Формулу называют элементарной конъюнкцией, или конъюнктом, если она является конъюнкцией переменных или их отрицаний.
Пример 3. Элементарные конъюнкции: Х2& Х3; Х1 &
Х3; Х1 &  Х2 & Х4 & Х2.
Х2 & Х4 & Х2.
Определение 14. Говорят, что формула находится в дизъюнктивной нормальной форме (ДНФ), если она является дизъюнкцией элементарных конъюнкций.
Пример 4. Рассмотрим формулу (X1 & Х2 &  Х3)
Х3) (X1&
(X1&  Х2 & Х3). Эта формула находится в ДНФ.
Х2 & Х3). Эта формула находится в ДНФ.
Справедлива следующая теорема, которую приведем без доказательства.
Теорема 5. Для любой формулы а можно найти такую формулу b, находящуюся в ДНФ, что а = b. В этом случае формула b называется дизъюнктивно нормальной формой формулы а.
Определение 15. Пусть формула ане содержит символов =>, ~ . Формула а* называется двойственной формуле а, если она получена из а одновременной заменой всех символов &,  на им двойственные, т. е. & на
на им двойственные, т. е. & на  ,
,  на &.
на &.
Определение 16. Говорят, что формула а находится в конъюнктивной нормальной форме (КНФ), если формула а* находится в ДНФ.
Сформулируем без доказательства еще одну важную теорему.
Теорема 6. Для любой формулы а можно найти такую формулу b, что b находится в КНФ и а = b. В этом случае формула b называется конъюнктивно нормальной формой формулы а.
Замечание 4. ДНФ и КНФ формулы а, не являются однозначно определенными. Кроме ДНФ и КНФ вводятся еще другие нормальные формы, например совершенные дизъюнктивные и конъюнктивные нормальные формы (СДНФ и СКНФ) [4, 6, 10, 11], как и для булевых функций (см. подразд. 6.2).
Законы логики высказываний. Тавтологии
Пусть формула а зависит от множества переменных Х1, ..., Хn.
Определение 17. Формула а называется тавтологией (или тождественно-истинной формулой), если на любых оценках списка переменных она принимает значение И, т. е. а≡И.
Здесь под оценкой списка переменных понимается сопоставление каждой переменной этого списка некоторого истиностного значения.
Формула а называется выполнимой, если на некоторой оценке списка переменных Х1, ...,Хп она принимает значение И. Формула а называется опровержимой, если на некоторой оценке списка переменных Х1, ...,Хп она принимает значение Л.
Формула а называется тождественно-ложной, если на любых оценках списка переменных Х1, ...,Хп она принимает значение Л, т. е. а≡Л.
Рассмотрим некоторые утверждения, являющиеся очевидными следствиями данных определений:
• а — тавтология тогда и только тогда, когда, а не является опровержимой;
• а - тождественно-ложна тогда и только тогда, когда а не является выполнимой;
• а — тавтология тогда и только тогда, когда  а тождественно-ложна;
а тождественно-ложна;
• а — тождественно-ложна тогда и только тогда, когда  а тавтология;
а тавтология;
• а ~ b — тавтология тогда и только тогда, когда а и b равносильны.
С точки зрения логики тавтология — не что иное, как логические законы, ибо при любой подстановке вместо переменных тавтологии конкретных высказываний получим истинное высказывание.
Основная проблема логики высказываний называется проблемой разрешимости. Она состоит в выяснении, является ли произвольная формула тавтологией. В логике высказываний всегда есть возможность (есть алгоритм) решить такую задачу. Например, решить ее можно:
использованием таблиц истинности (табличный способ);
приведением формулы к константе «И» с помощью правил равносильных преобразований (алгебраический способ);
имеются и другие способы.
Тем самым проблема разрешимости логики высказываний алгоритмически разрешима.
Пример 5. Доказать, что формула ( а =>
а => b) => (b => а) есть тавтология.
b) => (b => а) есть тавтология.
Используем алгебраический способ.
( а =>
а => b) => (b => а)≡(
b) => (b => а)≡(
 a
a
 b) => (b => а)≡
b) => (b => а)≡
≡(a
 b) => (
b) => ( b
b a) ≡
a) ≡ (a
(a
 b)
b)  (
( b
b a) ≡
a) ≡
≡( a&
a&
 b)
b)  (
( b
b a)≡(
a)≡( a & b)
a & b)
 b
b a≡
a≡
≡(( a
a
 b)&(b
b)&(b
 b))
b)) a≡(
a≡( a
a
 b)
b)  a≡
a≡
≡ a
a
 b
b a≡ (
a≡ ( a
a  a)
a) 
 b≡ И
b≡ И
 b ≡ И.
b ≡ И.
Рассмотрим две теоремы в тавтологиях [4, 10].
Теорема 7 (о простейших логических законах). Пусть а, b, с — произвольные формулы. Тогда:
1) a
 a — закон исключенного третьего (tertim non datur), его читают: «а или не а»;
a — закон исключенного третьего (tertim non datur), его читают: «а или не а»;
2) а => а (сравните с п. 1);
3) а => (b => а);
4) (а => b) => ((b => с) => (а => с)) — цепное рассуждение (пусть из а следует b; тогда, если из b, в свою очередь, следует с, то из а следует с);
5) (а=> (b => с)) => ((а => b) => (а => с)) (если из а следует, что b влечет с, то из того, что а влечет b, следует, что а влечет с);
6) (a&b)=> a; (a&b)=>b;
7) а => (b=>(a&b));
8) а => (а  b); b => (а
b); b => (а  b);
b);
9) ( b=>
b=> a) => ((
a) => (( b=> a) => b);
b=> a) => b);
10) ((a => b) => a) => a — закон Пирса.
Теорема 8 (о логических законах рассуждения от противного). Пусть a, b, с — произвольные формулы.Тогда тавтологиями будут:
11) (а=>b) ~ ( (a=>b)=>(с&
(a=>b)=>(с& с)) (утверждение «из а следует b» эквивалентно утверждению о том, что из отрицания этого следует ложь);
с)) (утверждение «из а следует b» эквивалентно утверждению о том, что из отрицания этого следует ложь);
12) (а=>b) ~ ( b =>
b => а) (утверждение, что из а следует b эквивалентно утверждению, что из
а) (утверждение, что из а следует b эквивалентно утверждению, что из  b следует
b следует  a);
a);
13) (a=>b) ~ ((а & b) =>
b) => а) (из а следует b тогда и только тогда, когда из а и отрицания b следует отрицание а);
а) (из а следует b тогда и только тогда, когда из а и отрицания b следует отрицание а);
14) (а => b) ~ ((а& b) =>b) (из а следует b в том и только в том случае, когда из а и отрицания b следует b).
b) =>b) (из а следует b в том и только в том случае, когда из а и отрицания b следует b).
Контрольные вопросы
Целое имеет такую же природу, как и Я, и что мы постигаем Целое путем все более глубокого постижения Я.
Лейбниц Г.В. Сочинения в 4 т. М.: Мысль, 1983. т. 2 с. 54.
Лекция № 13
ЛОГИКА ПРЕДИКАТОВ
Предикаты – это отображения произвольных множеств во множество высказываний. Логика предикатов представляет собой развитие логики высказываний. Исторически понятие о предикатах явилось следствием логического анализа высказываний, т.е. выяснения их логической структуры.
Определение предиката
Пример: «х простое число». Это выражение не является высказыванием, но если в нем переменную х заменить… Таким образом, выражение: «х простое число» можно рассматривать как функцию Р(х), зависящую от переменной х. Область…Рk(х1, х2, ..., хk): Мk → {1,0}.
Например, если Х — множество действительных чисел, то х2 > 1 — одноместный предикат.
Если X, У — множества действительных чисел, то ху = 5 — двуместный предикат.
Предикат называется разрешимым, если существуют такие кортежи, компоненты которых обращают предикат в истинное высказывание.
Если предикат при подстановке любых конкретных элементов из соответствующих множеств обращается в истинное высказывание, он называется тождественно истинным.
Если предикат при подстановке любых конкретных элементов из соответствующих множеств обращается в ложное высказывание, он называется тождественно ложным.
К предикатам, определенным на одном и том же множестве, можно применять операции алгебры высказываний: конъюнкцию, дизъюнкцию, импликацию, эквивалентность, отрицание и получать новые предикаты.
Например, если к предикатам «х = y» и «х < у» — обозначим их соответственно Р(х, у) и Q(x, у) — применить операцию конъюнкции, то получим новый предикат Р(х, у) Q(x, у).
Q(x, у).
Язык логики предикатов.
Символами X, Y, Z, Xi, Yi, ... в логике предикатов принято обозначать предметные переменные, т.е. отдельные предметы — имена. Они могут быть простыми и сложными. Если такие предметы (имена) не содержат дополнительной информации о себе, то они называются собственными (простыми), например «земля», «студент» и др. Если такое имя содержит наряду с самим предметом его отдельные свойства, то оно является сложным, например «автор романа «Анна Каренина», «перпендикулярные прямые», «взаимно-однозначное соответствие» и др.
Символами а, b, с, ai bi ... принято обозначать константы или предметные постоянные, т. е. конкретные значения имен предметов из указанной предметной области. Высказывательные формы, входящие в предикаты, называют также препозиционными функциями, или предикаторами.
Любое непустое множество содержит два подмножества: само себя и пустое. Это свойство автоматически выделяет из области определения два случая.
Тождественно-истинным называется предикат, истинный всюду на области определения: Т(Р) = D(P).
Тождественно-ложным называется предикат, множество истинности которого пусто: Т(Р) = 0.
Два предиката в одной и той же области определения различны в том и только в том случае, если их множества истинности не совпадают. Это определение совпадает с отрицанием обычного определения равенства функций.
Логические операции (связки) над предикатами
Связки, аналогичные связкам булевой алгебры и исчисления высказываний, соответствуют логическим операциям над предикатами. Операции над n-местными предикатами вводятся аналогично одноместным.
Пусть, например, Р(х, ...) и Q(x, ...) — предикаты, которые
определены на множестве D, причем Т(Р) и T(Q) — их множества истинности.
Отрицанием предиката Р(х,...) называется предикат Р(х), также определенный на множестве D и истинный при тех значениях переменной х, при которых Р(х, ...) ложен, т.е. Т(Р) = DT(P) (рис. 5.1).
Рассмотрим примеры.
1. Для предикатов Р(х): «х — четное число» и Q(x): «х кратно 7» конъюнкцией Р(х) л Q(x) служит предикат «х — четное и кратное 7 число» или «х — число, кратное 14».

Рис. 5.1. Множество истинности Рис. 5.2. Множество истинности
предиката Р(х) конъюнкции предикатов
Пример.
Предикат Р(х): «х — простое число» определен на множестве D = Z целых чисел, а его областью истинности являются только простые числа, т. е. числа, имеющие два делителя: х и 1. Тогда предикат «х — составное (целое) число», также определенный на Z, будет отрицанием предиката Р(х), т.е. 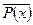 , а его областью истинности будет множество всех целых составных чисел (имеющих три и более делителей):
, а его областью истинности будет множество всех целых составных чисел (имеющих три и более делителей):  T(P).
T(P).
Аналогично вводятся и остальные операции.
Конъюнкция предикатов Р(х, ...) и Q(x, ...) есть новый предикат 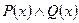 , определенный на множестве D и истинный при тех значениях переменной х, при которых истинны одновременно оба предиката Р(х, ...) и Q(x, ...), поэтому
, определенный на множестве D и истинный при тех значениях переменной х, при которых истинны одновременно оба предиката Р(х, ...) и Q(x, ...), поэтому 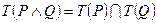 (рис. 5.2).
(рис. 5.2).
Пример.
Для предикатов P(x): «x – четное число» и Q(x): «x – кратное 7» конъюнкцией 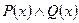 служит предикат «x – четное и кратное 7 число» или «x –число, кратное 14»
служит предикат «x – четное и кратное 7 число» или «x –число, кратное 14»
Пример.
Решить систему неравенств  означает: решить первое неравенство, т.е. определить Т(Р1), решить второе неравенство — определить Т(Р2):
означает: решить первое неравенство, т.е. определить Т(Р1), решить второе неравенство — определить Т(Р2): ,<=>
,<=> . Определить, при каких х верны и первое, и второе неравенства. В данном случае система
. Определить, при каких х верны и первое, и второе неравенства. В данном случае система  означает конъюнкцию высказываний
означает конъюнкцию высказываний 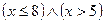 <=> 5 < х =< 8, а ответ является пересечением Т(Р1) и T(Р2) (рис. 5.3), т. е. интервалом 5 < х < 8.
<=> 5 < х =< 8, а ответ является пересечением Т(Р1) и T(Р2) (рис. 5.3), т. е. интервалом 5 < х < 8.
Рис. 5.3. Графическое решение системы неравенств 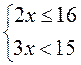
Обратите внимание, что в итоговый ответ вошла конъюнкция высказываний, эквивалентных данным в условии, а не самих исходных.
Дизъюнкцией предикатов Р(х, ...) и Q(x, ...) называется предикат Р(х)vQ(x), определенный на множестве D и истинный при тех значениях переменной х, при которых истинен хотя бы один из предикатов Р(х) или Q(x).
Поэтому  (рис. 5.4).
(рис. 5.4).

Рис. 5.4. Множество истинности дизъюнкции предикатов 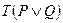
Пример.
Для предикатов Р(х): «х— число, кратное 3» и Q(x): «х — число, оканчивающееся на 3», определенных на N, дизъюнкцией Р(х)vQ(x) служит предикат: «х — число или кратное 3, или оканчивающееся цифрой 3».
Так, при решении уравнений (неравенств), левая часть которых есть произведение нескольких множителей, а правая — нуль, они разбиваются на совокупность уравнений (неравенств).
Пример.
х2 - 8х - 20 = 0 <=> (х - 10)(х + 2) = 0 <=> х - 10 = 0 (Р1)илих + 2 = 0 (Р2). Таким образом, нужно найти T(P1) = {10}, T(Р1) = {-2} и их объединение: Т(Р) = {-2, 10}.
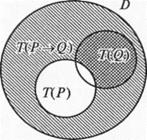 Импликацией предиката Р(х, ...) в Q(x, ...) называется предикат Р(х) → Q(x), определенный на множестве D и ложный только при тех значениях переменной х, при которой предикат Р(х, ...) истинен, а предикат Q(x, ...) ложен. В полном соответствии с формулой алгебры логики
Импликацией предиката Р(х, ...) в Q(x, ...) называется предикат Р(х) → Q(x), определенный на множестве D и ложный только при тех значениях переменной х, при которой предикат Р(х, ...) истинен, а предикат Q(x, ...) ложен. В полном соответствии с формулой алгебры логики  имеем:
имеем: 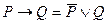 и
и  (рис. 5.5).
(рис. 5.5).
Рис. 5.5. Множество истинности импликации предикатов 
Пример.
Импликацией предикатов Р(х): «х — нечетное число» и Q(x): «х кратно 5», определенных на 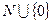 , служит предикат Р(х) → Q(x): «Если х — нечетное число, то х кратно 5».
, служит предикат Р(х) → Q(x): «Если х — нечетное число, то х кратно 5».
Здесь Т(Р) = {y|(ymod2) = 1} = {1, 3, 5, ...};
T(Q) = {y|(ymod5) = 0}= {0, 5, 10, ...}.
Тогда D/T(Р) = {у|(ymod2) = 0} ={0, 2, 4,...};
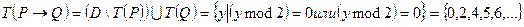
Импликация верна, если число кратно двум или пяти.
Замечание. Поскольку в данном нами алфавите связка → является основной, a  и
и  - дополнительными, то дадим введение конъюнкции и дизъюнкции через
- дополнительными, то дадим введение конъюнкции и дизъюнкции через 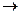 и
и 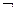 :
:
 ,
,
 .
.
Эквиваленцией предикатов Р(х, ...) и Q(x, ...) называется предикат Р(х) в Q(x), определенный на множестве D и истинный при тех значениях переменной х, при которых либо оба предиката истинны, либо оба предиката ложны.
Поэтому  .
.
В силу законов Де Моргана 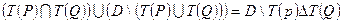 . Если Т(Р) = T(Q), то Т(Р = Q) = D.
. Если Т(Р) = T(Q), то Т(Р = Q) = D.
Пример.
Эквивалентны предикаты Р(х): «х — натуральное число, кратное 3» и Q{x): «х — натуральное число, сумма цифр которого делится на 3».
Кванторы
Помимо операций алгебры высказываний, в логике предикатов есть две операции, которые связаны с природой предикатов. Пусть дан предикат Р(х), зависящий от одной переменной и определенный на поле М.
а) Выражение ( х)Р(х) означает высказывание, истинное только в том случае, когда предикат Р(х) истинен для всех предметов из поля М. Выражение (
х)Р(х) означает высказывание, истинное только в том случае, когда предикат Р(х) истинен для всех предметов из поля М. Выражение ( х)Р(х) читается «для всякого х, Р(х)», здесь символ
х)Р(х) читается «для всякого х, Р(х)», здесь символ  — квантор общности.
— квантор общности.
б) Выражение ( х)Р(х) означает высказывание, истинное только в том случае, когда предикат Р(х) истинен хотя бы для одного предмета из поля М. Выражение (
х)Р(х) означает высказывание, истинное только в том случае, когда предикат Р(х) истинен хотя бы для одного предмета из поля М. Выражение ( х)Р(х) читается «существует х, что Р(х)», символ
х)Р(х) читается «существует х, что Р(х)», символ  — квантор существования.
— квантор существования.
Рассмотрим примеры применения операций квантирования к предикатам. Пусть даны предикаты над полем натуральных чисел:
1) х2 = х х, тогда ( х) (х2 = х х) — истинное высказывание;
х) (х2 = х х) — истинное высказывание;
2) х + 2 = 7, тогда ( х) (х+2 = 7) — ложное высказывание; а (
х) (х+2 = 7) — ложное высказывание; а ( х) (х + 2 = 7) — истинное высказывание;
х) (х + 2 = 7) — истинное высказывание;
3) х + 2 = х, тогда ( х) (х + 2 = х) — ложное высказывание.
х) (х + 2 = х) — ложное высказывание.
| Название | Прочтение | Обозначение |
| Квантор общности | «все», «всякий», «каждый», «любой» | 
|
| Квантор существования | «Хотя бы один», «найдется», «существует» | 
|
Квантор общности — это оператор, приводящий в соответствии любому заданному предикату у = Р(х) такую двузначную логическую переменную z, которая принимает значение 1 тогда и только тогда, когда у = 1при всех значениях х.
Квантор существования — это оператор, приводящий в соответствии любому одноместному предикату у = Р(х) такую двузначную логическую переменную z, которая принимает значение 0 тогда и только тогда, когда у = 0 при всех значениях х.
Рассмотрим некоторые общие свойства введенных операторов. В соответствии с определениями кванторов логическая переменная z в выражениях
z = ( х)Р(х)
х)Р(х)
z = ( х)Р(х)
х)Р(х)
уже не является функцией предметной переменной х.
Для того чтобы отметить отсутствие функциональной зависимости z от х, предметную переменную х в таких случаях называют связанной. Несвязанные переменные называют свободными.
Например, в предикате
( х) A(х,y)
х) A(х,y) (
( z) B(z,v)
z) B(z,v)
переменные хи z — связанные, а у и v — свободные.
Если квантор общности или квантор существования применяется не к одноместному предикату, а к какому-нибудь k-местному предикату, то в результате этого получается снова предикат, но за счет связывания одной предметной переменной получаемый предикат будет (k-1)-местным.
Кванторы.
Для количественных характеристик обычно используют понятия «все», «некоторые», «существуют» и др., которые называют кванторами (от лат. quantum — сколько). Мы часто пользовались символами  и
и  , заменяющими слова «любой» и «существует». Покажем действие этих кванторов в высказывательных формах. Часть формулы, на которую распространяется действие квантора, называется областью действия этого квантора. Вхождение переменной в формулу может быть связанным, если переменная расположена либо непосредственно после знака квантора, либо в области действий квантора, после которого стоит переменная. Все прочие вхождения — свободные. Например, в выражении
, заменяющими слова «любой» и «существует». Покажем действие этих кванторов в высказывательных формах. Часть формулы, на которую распространяется действие квантора, называется областью действия этого квантора. Вхождение переменной в формулу может быть связанным, если переменная расположена либо непосредственно после знака квантора, либо в области действий квантора, после которого стоит переменная. Все прочие вхождения — свободные. Например, в выражении 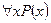 переменная х связывает свойство предиката и квантор общности. Грубо говоря, от этой переменной, ее конкретного вида и имени, ничего не зависит, т.е.
переменная х связывает свойство предиката и квантор общности. Грубо говоря, от этой переменной, ее конкретного вида и имени, ничего не зависит, т.е. 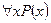 и
и  суть одно и то же. Так, можно произвольно называть индекс суммирования в рядах и переменную интегрирования в определенных интегралах. В частности, в определении множества как совокупности всех объектов, удовлетворяющих характеристическому свойству, использовалась запись G = {хР(х)}. Очевидно, что в предикате со связанной переменной ее так же легко можно заменить на любую другую. При этом множество все равно будет совокупностью тех же элементов, удовлетворяющих свойству Р. Переменная, не являющаяся связанной, называется свободной, если после подстановки вместо нее имени некоторых конкретных объектов предикат превращается в осмысленное предложение.
суть одно и то же. Так, можно произвольно называть индекс суммирования в рядах и переменную интегрирования в определенных интегралах. В частности, в определении множества как совокупности всех объектов, удовлетворяющих характеристическому свойству, использовалась запись G = {хР(х)}. Очевидно, что в предикате со связанной переменной ее так же легко можно заменить на любую другую. При этом множество все равно будет совокупностью тех же элементов, удовлетворяющих свойству Р. Переменная, не являющаяся связанной, называется свободной, если после подстановки вместо нее имени некоторых конкретных объектов предикат превращается в осмысленное предложение.
Между кванторами  и
и  и логическими операциями существует тесная связь. Пусть предикат Р(х) определен на конечном множестве D= {a1, а2, . . . ,аn}. Тогда высказывание
и логическими операциями существует тесная связь. Пусть предикат Р(х) определен на конечном множестве D= {a1, а2, . . . ,аn}. Тогда высказывание 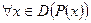 будет истинным только в том случае, если истинны одновременно все высказывания Р(а1), Р(а2),. . ., Р(ап), т.е. если истинна их конъюнкция:
будет истинным только в том случае, если истинны одновременно все высказывания Р(а1), Р(а2),. . ., Р(ап), т.е. если истинна их конъюнкция:  . Аналогично высказывание
. Аналогично высказывание 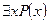 означает, что оно истинно, когда истинно хотя бы одно из высказываний Р(а1), Р(а2),…, Р(ап). Тогда должна быть истинной дизъюнкция высказываний
означает, что оно истинно, когда истинно хотя бы одно из высказываний Р(а1), Р(а2),…, Р(ап). Тогда должна быть истинной дизъюнкция высказываний  . Поэтому для конечной области определения выполняются равносильности:
. Поэтому для конечной области определения выполняются равносильности: 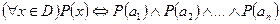 и
и  .
.
Таким образом, кванторы общности и существования являются дополнениями и аналогами соответственно логических операций конъюнкции и дизъюнкции.
Поскольку конъюнкцию можно выразить через отрицание и дизъюнкцию, то, вообще говоря, символ  можно было не включать в число основных символов, так как квантор существования
можно было не включать в число основных символов, так как квантор существования  по сути является сокращенной записью формулы
по сути является сокращенной записью формулы 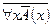 , выражающей так называемую двойственность.
, выражающей так называемую двойственность.
Пример.
Записать с помощью формул логики предикатов следующее утверждение: «Для лечения любого известного компьютерного вируса имеются программы. Существуют новые (неизвестные) компьютерные вирусы, для лечения которых программы еще не разработаны»
Решение.
Введем обозначения элементарных формул:
A(x) – известен компьютерный вирус x;
B(x) – для лечения вируса x существует программа;
Тогда с помощью логических связок и кванторов получим формулы:
 - против вируса x нет программы;
- против вируса x нет программы;
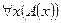 - любой вирус известен;
- любой вирус известен;
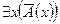 - существуют новые (неизвестные) вирусы;
- существуют новые (неизвестные) вирусы;
 - если вирус давно известен, то имеется программа для его лечения;
- если вирус давно известен, то имеется программа для его лечения;
 - существуют (появились) новые вирусы, для лечения которых программы еще не разработаны.
- существуют (появились) новые вирусы, для лечения которых программы еще не разработаны.
Тогда формализованное исходное утверждение примет вид:
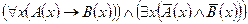
Отношение следования и равносильности между высказывательными формами связаны с тождественно-истинными импликацией и эквиваленцией, следовательно, их можно записать с помощью кванторов общности:
 тождественно
тождественно 
 тождественно
тождественно 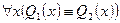
Пример.
Запись х2 - 5х = 0 <=> х(х - 5) = 0 является не формулой, а истинным высказыванием о равносильности двух формул, представленных в виде уравнений. В то же время справедлива запись 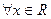 (х2 - 5х = 0) ≡ (х(х - 5) = 0), выражающая истинное высказывание, которое включает операцию эквиваленции в качестве составляющей.
(х2 - 5х = 0) ≡ (х(х - 5) = 0), выражающая истинное высказывание, которое включает операцию эквиваленции в качестве составляющей.
Поэтому логическое следование можно определить через импликацию, а равносильность через эквиваленцию. Так, для эквиваленции справедливо: «Две высказывательные формы Q1 и Q2 истинны или ложны (Q1 <=> Q2) одновременно с высказыванием 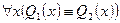 », что и было ранее введено.
», что и было ранее введено.
Существует различие в употреблении знаков и « »,«
»,«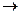 », «
», « » и «
» и «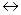 ».
».
Знаки «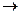 », «
», «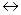 » обозначают логические операции импликации и равносильности и входят составной частью в формулы.
» обозначают логические операции импликации и равносильности и входят составной частью в формулы.
Знаки « » и «
» и « » обозначают определенные отношения между высказывательными формами, не входя в них в качестве составной части.
» обозначают определенные отношения между высказывательными формами, не входя в них в качестве составной части.
Квантификация многоместных высказывательных форм
Пусть Q(x1, х2, . . ., хn) — n-местная высказывательная форма. Ее замену на высказывательную форму  xi Q(x1, х2, . . ., хn) либо на
xi Q(x1, х2, . . ., хn) либо на  xi Q(x1, х2, . . ., хn) называют квантификацией высказывательной формы Q(x1, х2, . . ., хn) по переменной xi.
xi Q(x1, х2, . . ., хn) называют квантификацией высказывательной формы Q(x1, х2, . . ., хn) по переменной xi.
В процессе такой квантификации эта i-я переменная связывается одним из кванторов, а n-местная высказывательная форма превращается в (п-1)-местную.
Это аналогично тому, что если функцию f(x1, х2, …, хn) проинтегрировать от а до b по переменной xi, то полученный результат будет функцией от п-1 переменной и не будет зависеть от хi: I(х1,…, хi-1, xi+1, …, хn) =  Так, интеграл от функции одной (п = 1) переменной является константой и вообще ни от чего не зависит.
Так, интеграл от функции одной (п = 1) переменной является константой и вообще ни от чего не зависит.
Пусть дана двухместная высказывательная форма х - у < 0, определенная на  . Произведем квантификацию по переменной у («навесим» квантор общности). Получим одноместную высказывательную форму
. Произведем квантификацию по переменной у («навесим» квантор общности). Получим одноместную высказывательную форму 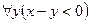 со свободной переменной х. Если для фиксированного х = х0 будет выполнено
со свободной переменной х. Если для фиксированного х = х0 будет выполнено  , то эта высказывательная форма превращается в истинное высказывание, например, при х = -2, а при х = 3 — в ложное.
, то эта высказывательная форма превращается в истинное высказывание, например, при х = -2, а при х = 3 — в ложное.
Если в одноместной высказывательной форме связать квантором и вторую переменную х, то можно получить высказывание: либо  — истинное высказывание;
— истинное высказывание;  — ложное высказывание.
— ложное высказывание.
При «навешивании» кванторов на двухместную высказывательную форму Q(x,у) можно получить одну из восьми комбинаций:
1) 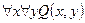 — «для любого х и любого у Q(x,у)»;
— «для любого х и любого у Q(x,у)»;
2)  — «для любого у и любого х Q(x,у)»;
— «для любого у и любого х Q(x,у)»;
3)  ) — «существует х и существует у, такие, что Q(x,у)»;
) — «существует х и существует у, такие, что Q(x,у)»;
4)  — «существует у и существует х, такие, что Q(x,у))»;
— «существует у и существует х, такие, что Q(x,у))»;
5) 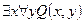 — «существует х, такой, что для любого у Q(x,у)»;
— «существует х, такой, что для любого у Q(x,у)»;
6) 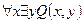 — «для всякого х существует у, такой, что Q(x,у)»;
— «для всякого х существует у, такой, что Q(x,у)»;
7) 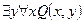 — «существует у, такой, что для любого х Q(x, у)»;
— «существует у, такой, что для любого х Q(x, у)»;
8) 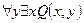 — «для всякого у существует х, такой, что Q(x, у)».
— «для всякого у существует х, такой, что Q(x, у)».
Очевидно, что первое и второе высказывания, а также третье и четвертое тождественны между собой, их значения истинности совпадают. Между остальными полученными высказываниями нельзя установить тождественности: если истинно высказывание 5, то истинным будет и высказывание 8, причем обратное неверно. Аналогично, если истинно высказывание 7, то истинно и высказывание 6, но не наоборот. То есть, если кванторы одноименны (1 — 4), то их порядок не играет роли и полученные высказывания эквивалентны. Если кванторы разноименные (5 — 8), то их порядок в полученном высказывании принципиально важен.
Например, для двухместного предиката «Город х находится в стране у» высказывание 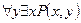 имеет вид 0-местного предиката и читается «В каждой стране у есть некоторый город х». Оно будет истинным, в то время как высказывание
имеет вид 0-местного предиката и читается «В каждой стране у есть некоторый город х». Оно будет истинным, в то время как высказывание 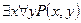 читается «Существует город х, находящийся во всех странах у» будет ложным.
читается «Существует город х, находящийся во всех странах у» будет ложным.
Пусть даны х, у — две различные переменные, F(x), Ф(х) и Q(x,у) — любые формулы логики предикатов и М — формула, не содержащая свободных вхождений х. Тогда справедливы равносильности, представленные с учетом двойственности кванторов  и
и  в табл. 5.5.
в табл. 5.5.
Таблица 5.5
Следствия и равносильности логики предикатов
Равносильности для 
| Правила | Равносильности для 
|
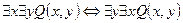
| Правила перестановки кванторов | 
|
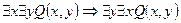
| ||

| Перенос отрицания с квантора на предикат | 
|

| 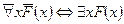
| |
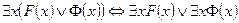
| 
| |
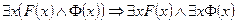
| 
| |

| 
| |

| 
|
Применение предикатов в алгебре
Типичным примером является уравнение, например, х2-Зх+2=0. Свободная переменная может принимать здесь любое числовое значение. Для некоторых чисел х… В приведенном выше примере множество U состоит из всех действительных чисел, а… В результате введения понятия множества истинности для предикатов мы сможем сказать, что решить уравнение — значит…Булева алгебра предикатов
Теорема. (Свойства логических операций для предикатов). Множество n-местных предикатов, определенных на X, образуют булеву алгебру…W(х1, х2, ..., хп); U(х,у),....
Применяя к переменным предикатам операции  ;
;  ; →; ↔; Ї;
; →; ↔; Ї;  ;
;  , получим формулы логики предикатов,
, получим формулы логики предикатов,
Формулой логики предикатов называется выражение, составленное из переменных предикатов с помощью логических операций и кванторов и обращающееся в конкретный предикат при подстановке вместо переменных конкретных предикатов.
Пример.
(( х) W(х, у)
х) W(х, у) В) → U(z) — формула логики предикатов. Формула логики предикатов называется тавтологией, если при подстановке любых конкретных предикатов она всегда обращается в тождественно истинный предикат.
В) → U(z) — формула логики предикатов. Формула логики предикатов называется тавтологией, если при подстановке любых конкретных предикатов она всегда обращается в тождественно истинный предикат.
Формулы
Определение формулы лежит в основе так называемой логики предикатов первого порядка, в которой разрешается квантифицировать (связывать кванторами) только предметные переменные. Логика предикатов первого порядка включает в себя все формулы логики высказываний, все равносильности исчисления высказываний, а также большинство правил вывода умозаключений из классической логики. Поэтому язык логики предикатов дает возможность анализировать рассуждения естественного языка и науки, делать выводы в различных формальных системах.
Так, высказывательная форма 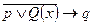 является формулой. В то же время высказывательная форма
является формулой. В то же время высказывательная форма 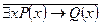 не будет формулой, поскольку в формуле
не будет формулой, поскольку в формуле 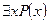 переменная х связана квантором существования, тогда как в формуле Q(x) эта же переменная свободна.
переменная х связана квантором существования, тогда как в формуле Q(x) эта же переменная свободна.
В чем ценность формальных теорий?
Для описания каких объектов используется логика предикатов?
Вообще говоря, ценность любой формальной теории заключается в возможности описывать с ее помощью произвольные объекты и связи между ними.
Теоремы.
К числу основных равносильностей логики предикатов относят:
1. 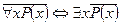 .
.
2. .
.
3. 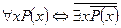 .
.
4.  .
.
5.  .
.
6.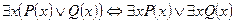 .
.
Сформулируем следующие правила.
(1) Формула логики предикатов называется атомарной, т.е. элементарной, если в ней нет связанных переменных.
(2) Пусть F — формула, тогда неF — тоже формула. Свободные и связанные переменные формулы неF — это соответственно свободные и связанные переменные формулы F.
(3) Пусть F и G — формулы, причем в них нет предметных переменных, которые были бы связаны в одной формуле и свободны в другой.
Тогда F G, F
G, F G, F→G, F↔G — формулы, в которых свободные переменные формул F и G остаются свободными, а связанные — связанными.
G, F→G, F↔G — формулы, в которых свободные переменные формул F и G остаются свободными, а связанные — связанными.
(4) Пусть F — формула, содержащая свободную переменную х. Тогда ( х)F, (
х)F, ( х)F — тоже формулы, в которых переменная х связана, а остальные свободные переменные, входящие в F, остаются свободными.
х)F — тоже формулы, в которых переменная х связана, а остальные свободные переменные, входящие в F, остаются свободными.
Заметим, что по определению формулы никакая переменная не может быть одновременно свободной и связанной.
Значение формулы определено лишь тогда, когда задана какая-то интерпретация входящих в нее символов.
Под интерпретацией понимают систему М=<М,f>, состоящую из непустого множества М и соответствия f, которое сопоставляет каждой формуле определенный предикат. При заданной интерпретации предметные переменные пробегают множество М, а логические символы и символы кванторов имеют свой обычный смысл.
Равносильные формулы логики предикатов
Пусть формулы F и G имеют одно и то же множество свободных переменных (в частности, пустое). Формулы F и G равносильны в данной интерпретации, если они принимают одинаковые значения на любом наборе свободных переменных, т. е. выражают в данной интерпретации один и тот же предикат.
Формулы F и G равносильны на множестве М, если они принимают одинаковые значения во всех интерпретациях заданных на множестве М.
Формулы F и G равносильны в логике предикатов, если они равносильны на всех множествах (F = G).
Рассмотрим правила перехода от одних формул к другим, им равносильным.
(1) Перенос квантора через отрицание. Пусть W(х) — формула, содержащая свободную переменную х. Тогда справедливы равносильности:
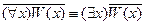 ,
,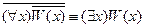 ,
,
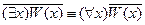 ,
, .
.
(2) Вынос квантора за скобки. Пусть формула W(х) содержит свободную переменную х, а формула В не содержит переменной х. Формулы W(х) и В удовлетворяют третьему правилу создания формул. Тогда справедливы равносильности:
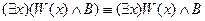 ,
,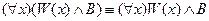 ,
,
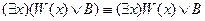 ,
,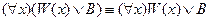 .
.
(3) Перестановка одноименных кванторов. Имеем
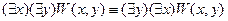 ,
,  .
.
(4) Переименование связанных переменных. Заменяя связанную переменную формулы W другой переменной, не входящей в эту формулу, в кванторе и всюду в области действия квантора, получим формулу, равносильную W.
Приведенные и нормальные формы в логике предикатов
Рассмотрим способ упрощения формул, опирающийся на приведенные равносильности.
Формулы, в которых из логических символов имеются только символы конъюнкция, дизъюнкция и отрицание, причем символ отрицания встречается над символами предикатов, будем называть приведенными.
Пример.
Формула ( x1) A1(1)(x2)
x1) A1(1)(x2)  (
( x1)не(А2(2)(x2,x3)) — приведенная;
x1)не(А2(2)(x2,x3)) — приведенная;
Формула не( x2) A1(1)(x2) → А2(1)(x1) — неприведенная.
x2) A1(1)(x2) → А2(1)(x1) — неприведенная.
Для любой формулы существует равносильная ей приведенная формула, причем множества свободных и связанных переменных этих формул совпадают.
Такая приведенная формула называется приведенной формой данной формулы.
В логике высказываний мы ввели две нормальные формы — дизъюнктивную нормальную форму и конъюнктивную нормальную форму.
В логике предикатов также имеется нормальная форма, цель которой — упрощение процедуры доказательств.
Приведенная формула называется нормальной, если она не содержит символов кванторов или все символы кванторов стоят впереди (т.е. логические символы и символы предикатов стоят в области действия каждого квантора).
Для любой приведенной формулы существует равносильная ей нормальная формула той же длины (под длиной формулы будем понимать общее число входящих в нее символов предикатов, логических символов и символов кванторов).
Нормальная формула называется нормальной формой данной формулы.
Приведем несколько формул, находящихся в нормальной форме:
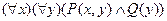 ,
, 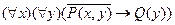 ,
,
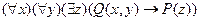 .
.
Алгоритм преобразования формул в нормальную форму
1. Исключить логические связки ↔ и → с помощью формул
F↔G=(F→G)(G→F), F→G=неFG.
не(FG) = неFнеG, не(FG) = неFнеG, законы , ,Исчисление предикатов
В исчислении предикатов, так же как и в исчислении высказываний, на первом по важности месте стоит проблема разрешимости. Но в исчислении высказываний проблема разрешимости состояла в решении вопроса… Теперь же вопрос следует поставить иначе. Принимает ли данная функция значение 1 при:Следование и эквиваленция
Пусть даны предикаты Q1(x1, х2, …, хn) и Q2(x1, х2, …, хn), а их множества истинности соответственно T(Q1) и T(Q2). Поскольку , то если , т.е. Q1… Пусть даны два предиката, определенные на одном множестве. Высказывательные… Пример.Литература
1. Акритас А. Основы комбинаторной алгебры с приложениями. – М.: Мир, 1994
2. Александров П.С. Введение в теорию множеств и общую топологию. М.: Наука, 1977. - 367 с.
3. Архангельский А.А. Канторовская теория множеств. М.: Изд-во Моск. ун-та, 1988, 112 с
4. Аляев Ю.А., Тюрин С.Ф. дискретная математика и математическая логика. - М.: Финансы и статистика, 2006. - 368 с.
5. Асанов М.О., Баранский В.А., Расин .В. Дискретная математика: графы, матроиды, алгоритмы. - Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001.
6. Ахо А., Ульман Дж. Теория синтаксического анализа, перевода и компиляции. М.: Мир, 1978 - с.
7. Ахо А., Хопкрофт Дж., Ульман Дж. Построение и анализ вычислительных алгоритмов. М.: мир, 1979. - с.
8. Басакер Р., Саати Т. Конечные графы и сети. – М.: Наука, 1974.
9. Бауэр Ф.Л., Гооз Г. Информатика. М.: Мир, 1990
10. Белешко Дмитрий ИНТЕРНЕТ
11. Белов В.В., Воробьев Е.М., Шаталов В.Е. Теория графов. – М.: Высш. Школа, 1976
12. Белоусов А.И., Ткачев С.Б. Дискретная математика. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2006. – 744 с.
13. Берж К. Теория графов и ее применение. Изд. Иностр. Лит., 1962
14. Бочаров В.А. Основы логики. М.: Логос, 1994. -296 с.
15. Владимиров Д.А. Булевы алгебры. М.: Наука, 1989. - 318 с.
16. Гаврилов С.П. Сапоженко А.А. Сборник задач по дискретной математике. – М.: Наука, 1978.
17. Гаврилов С.П. Сапоженко А.А. Задачи и упражнения по дискретной математике. – М.: Физматлит, 2006. – 416 с.
18. Галушкина Ю.И. Марьямов А.Н. Конспект лекций по дискретной математике с упражнений и контрольными работами. М.: Айрис ПРЕСС, 2007 – 175 с.
19. Ганчев И., Чимев К., Стоянов Й. Математический фольклор. М.: Знание, 1987.
20. Гиндикин С. Г. Алгебра логики в задачах. М.: Наука; 1972.
21. Горбатов В. А. Фундаментальные основы дискретной математики. М.: Наука; Физматлит, 2000.
22. Горбатов В.А. Основы дискретной математики. М.: Высшая школа, 1986. - 311 с.
23. Гэри М., Джонсон Д. Вычислительные машины и труднорешаемые задачи. М.: Мир, 1982
24. Деньдобренко Б. Н., Малика А.С. Автоматизация конструирования РЭА, М.: Высш. школа, 1980
25. Дискретная математика и математические вопросы кибернетики. Под ред. С.В. Яблонского и О. Б. Лупанова, Наука, 1974
26. Евстигнеев В.А. Применение теории графов в программировании. М.: Наука, 1985 – 352 с.
27. Емеличев В.А., Мельников О.И, Сарванов В.И., Тышкевич Р.И. Лекции по теории графов, М.: Наука, 1990
28. Ерусалимский Я. М. Дискретная математика. М.: Вузовская книга, 2005.
29. Ершов А. П. Введение в теоретическое программирование. М.: Наука, 1977
30. Ершов Д.Л., Палютин Е.А. "Математическая логика". - Спб.: Лань, 2004.
31. А.А. Зыков "Основы теории графов", М, Наука, 1987г.
32. Иванов Б.Н. Дискретная математика. Алгоритмы и программы. Полный курс. - М.: ФИЗМАТЛИТ, 2007. – 408 с.
33. Ивин А.А. Строгий мир логики. – М.: Педагогика, 1988. – 154 с.
34. Капитонова Ю.В., Кривой С.Л. и др. Лекции по дискретной математике. - СПб.: БХВ-Петербург, 2004. – 624 с.
35. Канцедал С.А. Дискретная математика.- М.: ИД «ФОРУМ» - ИФРА-М. 2007.
36. Каргаполов М. И., Мерзляков Ю. И. Основы теории групп. М.: Наука, 1977. - 239 с.
37. Карпов Ю.Г. Теория автоматов, Питер, 2002
38. Клашанов Ф.К. Дискретная математика, часть 1. Основы теории множеств и комбинаторика: Учебное пособие – М.: Изд-во МГСУ, 2010.
39. Кнут Д. Искусство программирования для ЭВМ Основные алгоритмы. Т.1, Мир, 1977
40. Кнут Д. Искусство программирования для ЭВМ Получисленные алгоритмы. Т.2, Мир, 1977
41. Кнут Д. Искусство программирования для ЭВМ Сортировка и поиск. Т.3, Мир, 1977
42. Козлова Е.Г. Сказки и подсказки. – М.: Мирос, 1994.
43. Кормен Т., Лейзерсон Ч., Ривест Р. Алгоритмы: построение и анализ. — М.: МЦНМО, 2001.
44. Кристофидес Н. Теория графов. Алгоритмический подход. М.: Мир, 1978. – 432 с.
45. Кон П. Универсальная алгебра, Мир, 1968
46. Кормен Т., Лейзерсон Ч., Ривест Р. Алгоритмы: построение и анализ. — М.: МЦНМО, 2001.
47. Кузнецов О. П. Дискретная математика для инженеров. М., 2005.
48. Кузнецов О.П., Адельсон-Вельский Г.М. Дискретная математика для инженера. – М.: Энергоатомиздат, 1988.
49. Кук Д., Бейз Г. Компьютерная математика. – М.: Наука, 1990.
50. Курейчик В.М. Математическое обеспечение конструкторского и технологического проектирования с применением САПР. – Радио и связь, 1990.
51. Лавров С.С., Гончарова Л.И. Автоматическая обработка данных, хранение информации в памяти ЭВМ, Наука 1988
52. Лавров И.А., Максимова Л. Л. Задачи по теории множеств, математической логике и теории алгоритмов. – М.: Наука 1984
53. Лекции по теории графов/ В. А. Емеличев, О.И. Мельников, В.И. Сарванов, Р. И. Тышкевич. – М.: Наука, 1990
54. Липский В. Комбинаторика для программистов. М.: Мир, 1988 – 213 с.
55. Логический подход к искусственному интеллекту /А. Тейз, П. Грибоман, Ж. Луи и др. – М.: Мир, 1990
56. Макоха А.Н., Сахнюк П.А., Червяков Н.И. Дискретная математика: Учебное пособие. – М.: ФИЗМАТЛИТ, 2005. – 368 с.
57. Мендольсон Э. Введение в математическую логику, Наука, 1984
58. Нечаев В.И. Элементы криптографии. Основы теории защиты информации, Высшая школа, 1999
59. Нефёдов В.Н., Осипова В.А. Курс дискретной математики М.: Изд-во МАИ, 1992.
60. Новиков Ф.А. Дискретная математика для программистов 2-е изд. – Спб.: Питер, 2004. – 364 с.
61. Общая алгебра. Т. 1,2/ О.В. Мельников, В.Н. Ремесленников, В.А. Романьков и др. М.: Наука, 1990.
62. Оре О. Теория графов. - М.: Наука, 1980.
63. Пойа Д. Математика и правдоподобные рассуждения. –м,6 Наука, 1975.
64. Райзер Г.Дж. Комбинаторная математика. М.: Мир, 1966 – 154 с.
65. Расёва Е., Сикорский Р. Математика метаматематики. М.: Наука, 1972. - 591 с.
66. Редькин Н.П. Дискретная математика: Курс лекций для студентов-механиков : учебное пособие. – Спб.: Издательство «Лань», 2006. - 96 с.
67. Рейнгольд Э., Нивергельт Ю., Део Н. Комбинаторные алгоритмы: теория и практика. -М.:Мир, 1980.
68. Романовский И. В. Дискретный анализ. СПб.—М., 2000.
69. Сачков В.Н. Введение в комбинаторные методы дискретной математики. Наука, 1977
70. Сачков В.Н. Введение в комбинаторные методы дискретной математики. Наука, 1982
71. В.Н. Сачков "Введение в комбинаторные методы дискретной математики", М, Наука, Электронная версия лекций Маркина П.М. по курсу "Дискретная математика" – На кафедральном сервере или в интернете.
72. Свами М., Тхуласираман К. Графы, сети и алгоритмы. – М.: Мир, 1984.
73. Спирина М.С. Дискретная математика : для студ. Учреждений сред. Проф. Образования/ М.С. Спирина, П.А. Спирин.- 4-е изд., испр. – М.: Издательский центр «Академия», 2007 г. – 368 с.
74. Соболева Т.С., Чечкин А.В. Дискретная математика: учебник для студ. вузов. – М.: Издательский центр «Академия», 2006. – 256 с.
75. Столл Р. Множества. Логика. Аксиоматические теории. – М.: Просвещение, 1968.
76. Судоплатов С.В., Овчинникова Е.В. Элементы дискретной математики. М.-Новосибирск: ИНФРД-М НГТУ, 2007.
77. Тей А. Логический подход к искусственному интеллекту/А.Тей, П. Грибомон. – М.: Мир, 1990.- 432 с.
78. Шапорев С. Д. Математическая логика. Курс лекций и практических занятий. СПб.: БХВ-Петербург, 2005.
79. Уилсон Р. Введение в теорию графов. Мир, 1977
80. Фрейденталь Х. Язык логики. –М.: Наука, 1969.
81. Фрид Э. Элементарное введение в абстрактную алгебру, Мир. 1979
82. Фридман М., Менон П. Теория и проектирование переключательных схем. – М.: Мир. 1978
83. Фудзисава Т., Касами Т. Математика для радиоинженеров. – М.: Радио и связь. 1984
84. Харари Ф. Теория графов. – М.: КомКнига, 2006. -296 с.
85. Холл М. Комбинаторика. – М.: Мир, 1970
86. Чень Ч., Ли Р., Математическая логика и автоматическое доказательство теорем. Наука, 1983
87. Шенфилд Дж., Математическая логика. – М.: Наука, 1975
88. Эрдниев М.П., Эрдниев Б.П. Укрупнение дидактических единиц как новая технология обучения математике. – М.: Просвящение, 1986.
89. Яблонский С.В. Введение в дискретную математику. М.: Высшая школа, 2003. - 384 с.
90. Ярцев Борис Интернет
91. http://catalog.unior.ru/resinfo.phtm?Res1D=474
92. http://abs.vvsu.ru/Books/Diskr_za/default.asp
93. http://mirea.boom.ru/diskret.htm1
94. http://www.mail.ru/k805/htm1/diskra.htm
95. http://rk-cmb.chat.ru/algo/ln_dm_01.htm
96. http://ulstu.ru/people/SOSNIN/umk/Basis_of_Artificial_Intelligence/m_lect.htm
97. http://www.auditorium.ru/books/339/philosophy/chap06.htm1#i06
98. http://www.isu.ru/slava/do/disc/curshome.htm
99. Harary F. Graph Theory. Reading, MA, Addison-Wesley, 1969 [Русский перевод Харари Ф. Теория графов. М.: Мир, 1973]
100. Oxley J. What is a matroid
101. Post E.L. The two-valued interactive systems of mathematical logic. – Annals of Math. Studies, v. 5, Princeton Univ. Press. Princeton-London, 1941).
ПРИЛОЖЕНИЕ
Буквы латинского алфавита

Представлен наиболее употребительный (но не единственный) вариант произношения (в частности, вместо „йот" иногда говорят „жи").

Наряду с указанным произношением также говорят „лямбда", „мю"и „ню".
Принятые обозначения
f(n) = О(g(п)) существуют константыС, N > 0, такие, что f(n) С g(п) для всех п N; f(n) = О(g(п)) <=> существуют константы С, N > 0, такие, что f(n) С… Конечно, f(n) = о(g(п)) тогда и только тогда, когда g(п) = О(f(n)). Символы О(g(п)) и о(g(п)) читаются соответственно:…Метаобозначения
– Конец работы –
Используемые теги: курс, лекций, дисциплине, Дискретная, математика0.091
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Курс лекций По дисциплине ДИСКРЕТНАЯ МАТЕМАТИКА
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов