Конспект лекций по дисциплине Линейная алгебра

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Государственное бюджетное образовательное учреждение

высшего профессионального образования

 

ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ

ФИНАНСОВО-ЭКОНОМИЧЕСКИЙИНСТИТУТ

Филиал в г. ТУЛЕ

__________________________________________________________________

Кафедра математики и информатики

 

Конспект лекций по дисциплине

«Линейная алгебра»

(для студентов бакалавриата, обучающимся по направлениям 080199.62 «Экономика», 080500.62 «Бизнес-информатика»)

 

Составил: к.ф.-м.н., доцент

кафедры математики и информатики

Луценко Алексей Георгиевич

 

 

Рассмотрено и одобрено на заседании кафедры

кафедры математики и информатики

протокол № ___ от «___»____________ 2011 г.

Тема 1: Матрицы и определители

Понятие матрицы. Виды матриц. Равенство матриц.

Транспонирование матрицы. Алгебраические операции над матрицами:

Умножение на число, сложение, умножение матриц

Определение 2.Две матрицы одного размера m´n называются равными, если они совпадают поэлементно, т.е. А=В Û aij=bij для любых… Определение 3.Матрица, состоящая из одной строки, называется матрицей-строкой… Определение 4.Матрица называется квадратной матрицей n-го порядка, если число ее строк равно числу ее столбцов и равно…

Определители 2-го и 3-го порядков (определение и их свойства).

Теорема Лапласа о разложении определителя по элементам строки или столбца

Определение 2.Определителем матрицы 3-го порядка A (определителем 3-го порядка) называется число, которое вычисляется по формуле . Заметим, что определитель 3-го порядка матрицы A есть алгебраическая сумма 3!=6 слагаемых, каждое из которых есть…

Свойства определителей

1.Если какая-либо строка (столбец) матрицы состоит из одних нулей, то ее определитель равен 0, 2.Если все элементы какой-либо строки (столбца) матрицы умножить на число l,… 3. При транспонировании матрицы ее определитель не изменяется, т.е. ½А'½=½A½.

Теорема Лапласа о разложении определителя

По элементам строки или столбца

Определение 2.Алгебраическим дополнением Aij элемента aij матрицы n-го порядка A называется его минор Mij , взятый со знаком (-1)i+j , т.е.… Теорема Лапласа.Определитель квадратной матрицы равен сумме произведений… ½A½=ai1×Ai1+ai2×Ai2+...+ain×Ain (разложение по элементам i-ой строки);

Особенная и неособенная квадратные матрицы. Присоединенная матрица. Матрица, обратная данной, и алгоритм ее вычисления

Определение 1.Квадратная матрица A называется особенной (вырожденной), если ее определитель равен нулю, т.е. ½A½=0.

Определение 2.Квадратная матрица A называется неособенной (невырожденной), если ее определитель отличен от нуля, т.е. ½A½¹0.

Определение 3.Матрица А^-1 называется обратной по отношению к квадратной матрице n-го порядка A, если A×А^-1=×А^-1×A=E, где E - единичная матрица n-го порядка.

Теорема(необходимое и достаточное условие существования обратной матрицы).Обратная матрица А^-1 существует (и единственна), тогда и только тогда, когда матрица A неособенная.

Алгоритм вычисления обратной матрицы

Если ½A½=0, то A - особенная матрица, А-1 не существует. Если ½A½¹0, то A - неособенная матрица, А-1 существует. 2. Находим матрицу A', транспонированную к А.

Вычисление ранга матрицы с помощью элементарных преобразований

Например, из матрицы A размером 3´4 можно получить миноры 1-го, 2-го и 3-го порядков. Определение 2.Рангом матрицы A называется наивысший порядок отличных от нуля… Ясно, что: 1) r(A) £ min (m, n);

Линейная независимость столбцов (строк) матрицы.

Теорема о ранге матрицы

Пусть дана матрица . Для ее строк введем обозначения: e1=(a11, a12, ... , a1n), e2=(a21, a22, ... , a2n), ..., em=(am1, am2, ... , amn) . Две строки матрицы называются равными, если равны их соответствующие… Операции умножения строки на число и сложения строк вводятся как операции проводимые поэлементно.

По формулам Крамера

. Умножим первое уравнение на a22, второе уравнение на (-a12) и сложим их.… Умножим первое уравнение на (-a21), второе уравнение на a11 и сложим их. Получим уравнение…

Система линейных однородных уравнений и ее решения.

Условие существования ненулевых решений системы

Определение 1. Cистома m линейных уравнений с n переменными называется системой линейных однородных уравнений, если все их свободные члены равны нулю

Такая система всегда совместна, так как имеет нулевое решение. Выясним, когда система линейных однородных уравнений имеет ненулевые решения.

Если m = n, а главный определитель системы отличен от нуля, то, по теореме Крамера, система имеет единственное решение, т.е. нулевое решение.

Следовательно, верна теорема

Теорема 1.Система линейных однородных уравнений имеет ненулевые решения тогда и только тогда, когда ранг ее матрицы при переменных меньше числа переменных, т.е. r(A)<n.

Тема 3: Векторные пространства

Векторы на плоскости и в пространстве (геометрические векторы). Линейные операции над векторами (сложение, умножение вектора на число). Коллинеарные и компланарные векторы

Определение 1.Вектором называется направленный отрезок AB с начальной точкой A и конечной точкой B (который можно перемещать параллельно самому себе).

Определение 2.Длиной вектора AB называется число çABç, равное длине отрезка AB, изображающего вектор.

Определение 3.Произведением вектора a на число l называется вектор b=l×a, имеющий длину çbç=l×çaç, направление которого совпадает с направлением вектора a, если l>0, и противоположно ему, если l<0.

Определение 4.Суммой двух векторов a и b называется вектор c=a+b, начало которого совпадает с началом вектора a, а конец - с концом вектора b при условии, что начало вектора b совпадает с концом вектора a. Вектор c в этом случае представляет собой диагональ параллелограмма, построенного на векторах a и b (правило параллелограмма).

Разностью двух векторов a и b называется сумма вектора a и вектора (-1)×b.

Определение 5. Векторы, лежащие на одной прямой (или на параллельных прямых) называются коллинеарными, векторы, лежащие в одной плоскости, называются компланарными.

Определение 6.Координатами вектора a называются координаты его конечной точки, если так переместить вектор параллельно самому себе, чтобы его начало совпало с началом координат.

На плоскости Oxy вектор имеет две координаты: a(x₁, y₁) и b(x₂, y₂).

В пространстве Oxyz вектор имеет три координаты: a(x₁, y₁, z₁) и b(x₂, y₂, z₂).

Линейные операции в координатной форме:

1) произведение вектора a=(x, y, z) на число l, есть вектор b=(l x, l y, l z);

2) суммой и разностью векторов a(x₁, y₁, z₁) и b(x₂, y₂, z₂) являются соответственно векторы c=a+b=(x₁+x₂, y₁+y₂, z₁+z₂) и d=a-b=(x₁-x₂, y₁-y₂, z₁-z₂);

Длина вектора a(x, y, z) вычисляется по формуле çaç = .

Скалярное произведение двух векторов (определение) и его выражение в координатной форме. Угол между векторами

(a, b) = çaç×çbç×cos j . В координатной форме скалярное произведение двух векторов равно сумме… Если a(x1, y1) и b(x2, y2), то (a, b) = x1×x2 + y1×y2 .

Векторное (линейное) пространство, его размерность и базис.

Теорема о существовании и единственности разложения вектора

Линейного пространства по векторам базиса

Определение 2.Линейное пространство называется n-мерным, если в нем существует n линейно независимых векторов, а любые из (n + 1) векторов являются… Определение 3.Совокупность n линейно независимых векторов n-мерного… Теорема 1. Каждый вектор линейного пространства можно представить и притом единственным образом в виде линейной…

Евклидово пространство. Длина (норма) вектора

Определение 1.Скалярным произведением двух векторов x = (x₁, x₂, … x_n) и y = (y₁, y₂, … y_n) n-мерного пространства называется число

(x, y) = x₁×y₁ + x₂×y₂ + … + x_n×y_n .

Определение 2.Евклидовым пространством называется линейное (векторное) пространство, в котором задано скалярное произведение векторов, удовлетворяющее определенным условиям (аксиомам).

Определение 3.Длиной (нормой) вектора в евклидовом пространстве называется корень квадратный из его скалярного квадрата

.

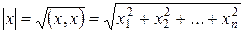Ортогональные векторы. Ортогональный и ортонормированный базисы. Теорема о существовании ортонормированного базиса

В евклидовом пространстве

Определение 2. Базис линейного пространства e1, e2, ..., en называется ортогональным, если (ei, ej)=0 при всех i≠j. Определение 3. Базис линейного пространства e1, e2, ..., en называется… Теорема 1. Во всяком n-мерном евклидовом пространстве существует ортонормированный базис (без доказательства).

Определение оператора. Понятие линейного оператора.

Образ и прообраз векторов

Определение 2.Оператор называется линейным, если для любых векторов x и y пространства Rn и любого числа a выполняются соотношения: 1) A(x+y) = A(x) + A(y) – свойство аддитивности оператора; 2) A(a×x) = a×A(x) – свойство однородности оператора.

Нулевой и тождественный операторы

Рассмотрим далее отображение линейного пространства Rⁿ в себя. Зафиксируем базис e₁, e₂, ... , e_n этого пространства.

Связь между вектором x и его образом A(x) можно выразить в матричной форме уравнением Y= A×X, где A – матрица линейного оператора A в заданном базисе, X = (x₁, x₂, … x_n)¢, Y = (y₁, y₂, … y_n)¢ - матрицы-столбцы из координат векторов x и y.

Теорема 1. Каждому линейному оператору линейного пространства Rⁿ в себя соответствует матрица в данном базисе. Обратно, всякой матрице n-го порядка соответствует линейный оператор n-мерного пространства.

Доказательство основано на теореме о единственности разложения вектора линейного пространства по базису и свойствах аддитивности и однородности линейного оператора.

Пусть x = x₁ e₁+x₂ e₂+ ... +x_n e_n. Тогда A(x) = x₁ A(e₁) + x₂ A(e₂) + ... +x_n A(e_n) = =x₁(a₁₁ e₁+a₂₁ e₂+…+a_n1 e_n)+ x₂(a₁₂ e₁+a₂₂ e₂+…+a_n2 e_n)+ ... +x_n(a_1n e₁+a_2n e₂+…+a_nn e_n) =

= (a₁₁ x₁+a₁₂ x₂ +…+a_1n x_n) e₁+ (a₂₁ x₁+a₂₂ x₂ +…+a_2n x_n) e₂+ (a_n1 x₁+a_n2 x₂ +…+a_nn x_n) e_n.

С другой стороны, y = y₁ e₁+ y₂ e₂+ ... + y_n e_n.

Следовательно,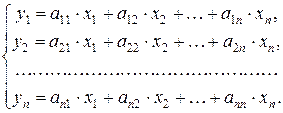

Определение 1.Ранг матрицы A называется рангом оператора A.

Определение 2. Суммой двух линейных операторов A и B называется оператор (A + B), определяемый равенством (A + B)(x) = A(x) + B(x).

Определение 3. Произведением линейного оператора A на число l называется оператор lA, определяемый равенством lA(x) =l(A(x)).

Определение 4. Произведением двух линейных операторов A и B называется оператор (AB), определяемый равенством (AB)(x) = A(B(x)).

Определение 5. Нулевым оператором называется оператор, переводящий все векторы пространства Rⁿ в нулевые векторы.

Определение 6. Тождественным оператором называется оператор E, переводящий каждый вектор в себя, то есть E(x) = x.

Собственные векторы и собственные значения матрицы.

Собственные векторы и собственные значения оператора (матрицы А). Характеристический многочлен оператора

И его характеристическое уравнение

Можно доказать, что ненулевое решение уравнения A×X = l×X существует тогда и только тогда, когда определитель çA -… Определение 2.Определитель çA - l×Eç является многочленом… Определение 3.Характеристическим уравнением линейного оператора A называется уравнение çA -…

Матрица линейного оператора в базисе,

Состоящем из его собственных векторов

Матрица A линейного оператора A пространства Rⁿ в себя принимает наиболее простой вид, если базис пространства состоит из собственных векторов оператора A.

Можно доказать, что в этом случае матрица A линейного оператора является диагональной и имеет вид:

.

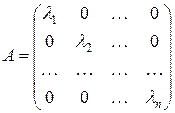Верно и обратное: если матрица A линейного оператора A в некотором базисе является диагональной, то все векторы этого базиса являются собственными векторами оператора A.

Тема 5: Квадратичные формы

Квадратичная форма (определение). Матрица квадратичной формы.

Ранг квадратичной формы

. Определение 2. Матрицей квадратичной формы L(x1, x2, … , xn) от n переменных… .

Квадратичная форма (канонический вид). Приведение квадратичной формы к каноническому виду. Закон инерции квадратичных форм

Определение 1. Квадратичная форма L(x₁, x₂, … , x_n) от n переменных называется канонической, если все её коэффициенты при произведениях различных переменных равны нулю, т.е. a_ij=0 при i¹j.

В этом случае квадратичная форма имеет вид .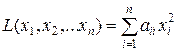

Доказано, что любая квадратичная форма с помощью линейного невырожденного преобразования может быть приведена к каноническому виду.

При этом её матрица приводится к диагональному виду.

Теорема 1 (закон инерции квадратичных форм). Ранг квадратичной формы не меняется при линейных преобразованиях.

Следовательно, ранг квадратичной формы L(x₁, x₂, … , x_n) от n переменных равен числу отличных от нуля коэффициентов канонической формы и совпадает с рангом соответствующей диагональной матрицы.

Положительно и отрицательно определенная, знакоопределенная квадратичные формы. Критерии знакоопределенности квадратичной формы (через собственные значения ее матрицы и по критерию Сильвестра)

Определение 1.Квадратичная форма называется положительно (отрицательно) определенной, если при всех значениях переменных, из которых хотя бы одно отлично от нуля, выполняется неравенство

L(x₁, x₂, … , x_n)>0 (L(x₁, x₂, … , x_n)<0).

Теорема 1 (критерий определенности квадратичной формы). Для того чтобы квадратичная форма L=X¢AX была положительно (отрицательно) определена, необходимо и достаточно, чтобы все собственные значенияl_i матрицы A были положительны (отрицательны).

Теорема 2 (критерий Сильвестра). Для того чтобы квадратичная форма L=X¢AX была положительно определена, необходимо и достаточно, чтобы все главные миноры матрицы A были бы положительны, т.е.

, , …, .

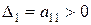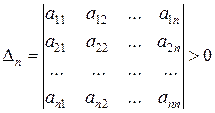Для того чтобы квадратичная форма L=X¢AX была отрицательно определена, необходимо и достаточно, чтобы знаки главных миноров матрицы A чередовались, начиная со знака «минус» для минора первого порядка, т.е.

, , и т.д.

Тема 6: Элементы аналитической геометрии

Уравнение линии на плоскости. Точка пересечения двух линий.

Основные виды уравнений прямой на плоскости (одно из них вывести)

Если из этого уравнения выразить переменную y, то получится уравнение y=f(x). Если линии заданы уравнениями, то точкой пересечения двух линий называется… Основные виды уравнений прямой на плоскости:

Общее уравнение прямой на плоскости, его исследование.

Условия параллельности и перпендикулярности прямых

Теорема 1.Любая прямая на плоскости может быть задана общим уравнением. Если В¹0, то , т.е. y=кх+b . При этом: а) если А=0, то y=b;

Кривые второго порядка, их общее уравнение.

Нормальное уравнение окружности. Каноническое уравнение эллипса. Геометрический смысл параметров окружности и эллипса

Ax2 + Bxy + Cy2 + Dx + Ey + F = 0, где A, B, C, D, E, F – действительные числа, причем A, B и C одновременно не… Определение 2. Уравнение Ax2 + Bxy + Cy2 + Dx + Ey + F = 0 называется общим уравнением кривой второго порядка.

Канонические уравнения гиперболы и параболы,

Геометрический смысл их параметров. Уравнение асимптот гиперболы.

График обратно пропорциональной зависимости и квадратного трехчлена

½½F1M½ - ½F2M½½ = 2a. Точки F1(c,0) и F2(-c,0) называются фокусами гиперболы. Определение 2. Каноническим уравнением гиперболы (в канонической системе координат) называется уравнение .

Общее уравнение плоскости в пространстве и его частные случаи. Нормальный вектор плоскости.

Условия параллельности и перпендикулярности двух плоскостей

Основные виды уравнений плоскости в трехмерном пространстве: 1) z = 0 - уравнение плоскости Oxy; 2) y = 0 - уравнение плоскости Oxz;

Уравнения прямой линии в пространстве как линии пересечения двух плоскостей. Канонические уравнения прямой. Направляющий вектор прямой. Условия параллельности и перпендикулярности двух прямых в пространстве

Существует несколько способов задания прямой в трехмерном пространстве:

1) - прямая как линия пересечения двух плоскостей задается аналитически системой двух линейных уравнений;

2) 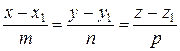- канонические уравнения прямой, где (m, n, p) – направляющий вектор прямой (т.е. прямая параллельна этому вектору), M₁(x₁, y₁, z₁) – некоторая точка, лежащая на данной прямой.

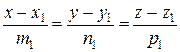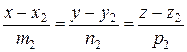Если две прямые заданы каноническими уравнениями и , то:

- прямые параллельны тогда и только тогда, когда их направляющие векторы коллинеарны: ;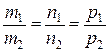

- прямые перпендикулярны тогда и только тогда, когда скалярное произведение их направляющих векторов равно нулю: m₁m₂ + n₁n₂ + p₁p₂ = 0;

Углы между двумя плоскостями, между двумя прямыми, между прямой и плоскостью. Условия параллельности и перпендикулярности двух плоскостей, двух прямых, прямой и плоскости

Если две плоскости заданы общими уравнениями A₁x + B₁y + C₁z + D₁ = 0 и A₂x + B₂y + C₂z + D₂ = 0, то угол j между плоскостями равен углу между нормальными векторами (A₁, B₁, C₁) и (A₂, B₂, C₂), следовательно,

.

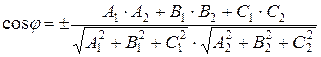Если две прямые заданы каноническими уравнениям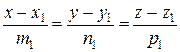и и 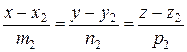, то угол j между прямыми равен углу между направляющими векторами (m₁, n₁, p₁) и (m₂, n₂, p₂), следовательно,

.

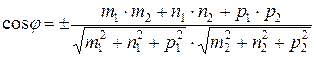Если плоскость задана общим уравнением Ax + By + Cz + D = 0, а прямая задана каноническими уравнениями 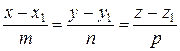, то угол j между прямой и плоскостью равен дополнительному углу к углу между нормальным вектором (A, B, C) и направляющим вектором (m, n, p), следовательно,

.

В последнем случае:

- плоскость и прямая параллельны тогда и только тогда, когда скалярное произведение их нормального и направляющего векторов равно нулю:

Am + Bn + Cp = 0.

- плоскость и прямая перпендикулярны тогда и только тогда, когда их нормальный и направляющий векторы коллинеарны:

.