рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Философия
- /
- К а с а т е л ь н ы х
Реферат Курсовая Конспект
К а с а т е л ь н ы х
К а с а т е л ь н ы х - раздел Философия, Основы информационных технологий и программирование Метод Касательных , Называемый Также Методом Ньютона, Широко ...
Метод касательных , называемый также методом Ньютона, широко используется при построении итерационных алгоритмов. Его попу-лярность объясняется быстрой сходимостью при хорошем начальном приближении . Метод Ньютона основан на замене небольшой дуги кривой у=f(х) касательной , проведенной в некоторой точке этой кривой (Рис. 2) .
Зададимся некоторой точкой хо ,уо , лежащей на кривой у=f(х) , и найдем уравнение касательной к этой кривой в выбранной точке. Касательная имеет наклон к оси абсцисс , обусловленный видом кривой f(х), т.е. при проведении касательной , кроме координат точки , должен быть выдержан и угол наклона кривой в выбранной точке. Таким образом, уравнение касательной - это уравнение прямой , проходящей через заданную точку с заданным угловым коэффициентом . Общий вид такого уравнения известен из курса аналитической геометрии :
у – уо = к ( х – хо) , ( 1 )
где к- угловой коэффициент, т.е. тангенс угла между прямой и осью х.
Найдем точку пересечения этой прямой с осью абсцисс . Для точки , лежащей на оси х , у = 0 . Подставляя это значение у в ( 1 ) , получаем
- уо = кх - кхо ; кхо - уо = кх ; х = хо - уо / к . ( 2 )
Поскольку точка ( хо , уо ) лежит на кривой у = f (х) , то уо = f (хо) , а
к = tga = dy / dx = f ‘(x o) . Подставляя найденные значения уо и к в формулу ( 2 ) , получаем :
х = хо - f’(хо) / f (хо) ( 3 )
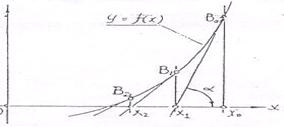
Рис. 2
Для выбора начального приближения в методе Ньютона необходимо проверить выполнения условия:
f (с) / (с) > 0, с = b или с = а. (4)
касательная к точке C проводится со стороны выпуклости функции. За начальное приближение итерационного процесса выбирается тот из конца отрезка (а, b) в котором выполняется условие (4).
Найденное значение х считаем значением корня уравнения у = f (х) в первом приближении , т.е. х1 = х0 – f(хо) / f’ (хо ). Для получения корня во втором приближении надо найти значение функции f ( х1) , провести каса-
тельную к кривой f (х) в точке В1 ( х1 , у1 ) и найти точку пересечения новой касательной с осью х . Абсцисса этой точки найдется по формуле
х2 = х1 - f(х1) /f’ (х1)
Обобщая эту формулу , можно для любого приближения записать
хn+1 = xn – f(xn) / f‘(xn) . ( 4 )
Процесс вычислений по формуле (4) прекращается , если два после-довательных значения х близки, т.е. если ½хn+1 – хn½£ e , где e - малое число, определяющее требуемую точность решения уравнения . Процесс вычислений может быть прекращен и в том случае , если ½f(хn+1)½£ e1 .
Скорость сходимости процесса последовательных приближений по методу Ньютона в большой мере зависит от удачного выбора исходной точки . Если численное значение производной f' (х) вблизи кор-ня мало, то процесс вычисления корня может оказаться длительным . Если же в окрестности корня график функции имеет большую крутизну, то процесс быстро сходится. Следовательно, если определен отрезок , внутри которого находится корень уравнения, то в качестве начального приближения корня следует принять тот конец отрезка , на котором модуль первой производной½f' (х)½ имеет большее значение .
Из всего сказанного следует , что для решения уравнений методом Ньютона необходимо иметь : уравнение функции f(х) , уравнение производной f' (х) , начальное приближение корня уравнения хо , значение малой величины e , определяющей момент выхода из итерационного процесса , счетчик итераций , позволяющий автоматически прервать расчет , если количество итераций превысит заданное значение . Алгоритм решения уравнения может быть представлен в следующем виде :
1) выбрать начальное значение корня хn ;
2) по формуле ( 4 ) вычислить хn+1 ;
3) если ½хn+1 - xn½£ e , то перейти к п. 7;
4) вычислить f (xn+1 ) ;
5) если ½f (xn+1 )½£ e , то перейти к п. 7 ;
6) положить хn = xn+1 и перейти к п. 2 ;
7) закончить расчет .
Этот алгоритм реализован в виде подпрограммы SUBROUTINE NEWTO ( A, B, EPS, X, K ).Текст подпрограммы приведен в приложении 4 .
– Конец работы –
Эта тема принадлежит разделу:
Основы информационных технологий и программирование
Министерство образования и науки... молодежи и спорта Украины... Национальный университет кораблестроения Херсонский филиал...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: К а с а т е л ь н ы х
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов