П р о с т ы х и т е р а ц и й

Этот метод решения уравнения f(х) = 0 состоит в замене исходного уравнения эквивалентным ему уравнением х = j(х) и построении последовательности х_n+1 = j (х_n) , сходящейся к точному решению при n®¥ . Достаточным условием сходимости является выполнение неравенства ½j¹(х)½< 1 на отрезке (а, в) . Поэтому прежде чем проводить вычисления корня, необходимо проверить выполнение условия сходимости вычислением значения j¹ (х) на концах отрезка (а , в) . Если ½j¹(а)½<1 и ½j ¹(в)½<1 , то можно начинать вычисления корня уравнения .

Может оказаться, что функция j (х) такова , что ее первая производная всегда > 1 по модулю.

В таком случае следует поискать такое преобразование функции j(х) , чтобы у преобразованной функции j₁(х) выполнялось условие

½j₁¹ (х)½< 1. Если такое преобразование найти не удалось, то уравнение следует решать каким – либо другим методом .

Пример . Установить можно ли решить уравнение е^х – х – 2 = 0 методом простых итераций.

В п. 2.2. (пример 4) было установлено , что один из корней рассматриваемого уравнения находится на отрезке ( 1; 2 ) . Преобразовываем исходное уравнение к виду , удобному для решения методом простых итераций : х = е^х – 2 . В этом уравнении j(х) = е^х – 2 . Находим первую производную функции j (х) : j¹ (х) = е^х . При х > 0 е^х >1 , следовательно , уравнение х = е^х - 2 методом простых итераций решить нельзя. Значит, первоначальное уравнение надо преобразовать к другому виду .

Запишем первоначальное уравнение в следующем виде е^х= х + 2 . Логарифмируя правую и левую части , получаем х = ln(х+2) . Теперь j (х) = ln(х+2) , j¹(х) = 1 / (х+2) . При х > 0 ½j¹ (х)½< 1 , т.е. теперь процесс итераций будет сходящимся , и уравнение можно решать методом простых итераций.

Когда сходимость процесса установлена , задаются начальным значением корня х_о и вычисляют первое приближение корня х₁= j (х_о) . Если ½х₁ – х_о½> e , то выполняют очередную итерацию х₂ = j (х₁) и т. д. Если после выполнения nитераций окажется , что ½х_n+1- х_n½< e , то вычисления заканчивают и за приближенное значение корня уравнения f(х) = 0 принимают величину х_n+1 . Из цикла вычисления корня уравнения можно выйти и в том случае , если значение первоначальной функции f(х) будет мало отличаться от нуля , т.е. если f (x_n+1)½£ e.

Из сказанного выше видно , что для решения уравнений методом простых итераций необходимо иметь: первоначальное уравнение f(х) = 0 , эквивалентное уравнение х = j (х) , выражение первой призводной эквивалентного уравнения j¹(х) , начальное приближение корня х_о и значение малой величины e , определяющей момент выхода из итерационного процесса .

Если отрезок ( а , в ) , содержащий корень уравнения f (х) = 0 , определен , то алгоритм решения уравнения может быть представлен в следующем виде :

1) вычислить значения j¹(х) на концах отрезка ( а , в ) ;

2) если ½j¹(а)½>1 или ½j¹(в) ½>1 , то перейти к п. 9 ;

3) выбрать начальное значение корня а £ х_n £ в ;

4) вычислить х_n+1 = j (х_n)

5) если ½х_n+1 – х_n½£ e , то перейти к п. 9 ;

6) вычислить f (х_n+1) ;

7) если ½f (x_n+1)½£ e , то перейти к п. 9 ;

8) положить х_n = х_n+1 и перейти к п. 4 ;

9) закончить расчет.

Этот алгоритм реализован в виде подпрограммы SUBROUTINE PRITE ( A, B, EPS, X, K ) .

Текст этой подпрограммы и пример решения уравнения методом простых итераций приведен в приложении 5.

Метод допускает простую геометрическую интерпретацию. Построим графики функций у = х и у = j (х). Корнем ξ уравнения х = j (х) является абсцисса точки пересечения кривой у = j (х) с прямой у = х (рис. 3). Взяв в качестве начальной произвольную точку х₀ ε [a, b], строим ломанную линию (рис. 3, а, б). Абсциссы вершин этой ломанной представляет собой последовательные приближения корня ξ.

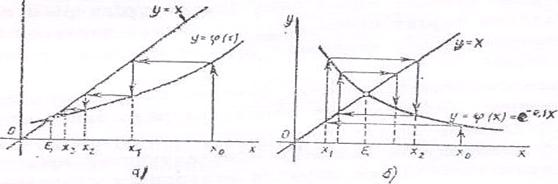
Рис. 3