рефераты конспекты курсовые дипломные лекции шпоры

Раздел Философия
/
Общие замечания.

Реферат Курсовая Конспект

Выберите учебное заведение

Общие замечания.

Общие замечания. - раздел Философия, Основы информационных технологий и программирование Если Функция ...

Если функция 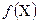непрерывна на отрезке 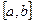и известна ее первообразная 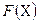, то определенный интеграл от этой функции в пределах от до 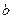может быть вычислен по формуле Ньютона-Лейбница:

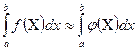(1).

Однако, во многих случаях первообразная функция 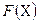не может быть найдена с помощью элементарных средств или является слишком сложной. Вследствие этого вычисление определенного интеграла по формуле (1) может быть затруднительным или даже практически невыполнимым. Кроме того, подынтегральная функция может быть задана таблично и тогда само понятие первообразной теряет смысл. Поэтому, важное значение имеют приближенные и в первую очередь численные методы вычисления определенных интегралов.

Задача численного интегрирования функции заключается в вычислении значения определенного интеграла на основании ряда значений подынтегральной функции. Численное определение однократного интеграла называется механической квадратурой, двойного – механической кубатурой, а соответствующие этим вычислениям формулы называются соответственно квадратурными и кубатурными формулами.

Мы рассмотрим только вычисление однократных интегралов. Обычный прием механической квадратуры состоит в том, что данную функцию 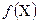на рассматриваемом отрезке 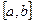заменяют интегрирующей или аппроксимирующей функцией 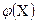простого вида ( например, полиномом ), а затем приближенно полагают:

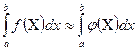(2).

При этом функция 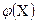должна быть такова, чтобы интеграл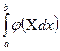

вычислялся непосредственно. На практике наиболее часто кривую, заданную уравнением 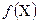, заменяют ломаной или параболой. И, соответственно, интеграл, выражаемый формулой (2), вычисляют методом трапеций методом Симпсона.

5.2. Вычисление определенных интегралов методом трапеций.

Определенный интеграл численно равен площади криволинейной

трапеции ABCD, которая ограничена осью абсцисс, двумя

ординатами 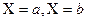и подынтегральной кривой .

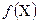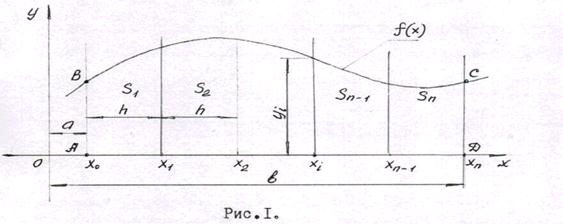
Для вычисления интеграла промежуток 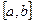делится на n равных частей. Длину каждой части обозначим через h .Тогда получаем 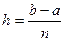;начальное значение равно абсцисса любой точки деления определится формулой 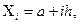значение подынтегральной функции в любой точке деления можно вычислить по формуле 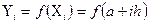. Если даже функция 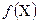задана графически, то значение можно снять с рисунка.

Из рисунка I видно, что площадь криволинейной фигуры ABCD являете:

суммой площадей трапеций высоты которых одинаковы и равны. Следовательно, можно записать

Если в числителе полученной формулы добавить и вычесть крайние ординаты, то получим

(3).

Из рис.2 видно, что формула (3) дает значение площади криволинейной фигуры с недостатком, если кривая выпукла вверх, и с избытком, если крива выпукла вниз. Для уменьшения погрешностей вычисления следует увеличив количество ординат, вводимых в расчет. При большом количестве ординат n

и соответственно при малом шаге h точность формулы (3) возрастает. Однако, ошибки округлен при вычислении значений функции 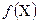.Поэтому оптимальное значение n зависит от того, с каким количеством верных значащих цифр производятся вычисления. Например, в судостроении, где широко применяется метод трапеций, обычно применяют 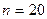. Эта традиция сложилась в те времена, когда все вычисления проводились с помощью арифмометра и логарифмической линейки с точностью до 3-4 значащих цифр.

Развернуть

Открыть в широком формате

– Конец работы –

Эта тема принадлежит разделу:

Основы информационных технологий и программирование

Министерство образования и науки... молодежи и спорта Украины... Национальный университет кораблестроения Херсонский филиал...

Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Общие замечания.

Что будем делать с полученным материалом:

Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:

Все темы данного раздела:

Методические указания
для самостоятельной работы студентов при изучении дисциплины «Основы информационных технологий и программирование» (численные мето

I. Некоторые сведения о приближенных вычислениях
1.1.Общие сведения о погрешностях В большинстве случаев технические вычисления производятся с приближенными числами. Это происходит потому, что исходные данные для численного определения

О т д е л е н и е к о р н е й
Пусть дано уравнение f(x)=0, в котором функция f(x) определена и непрерывна в некотором конечном или бесконечном интервале а<x<в. Всякое значение z , обращающее функцию f(x) в нуль, т.е. тако

П о л о в и н н о г о д е л е н и я .
Пусть дано уравнение f (x)= 0 , ( 1 ) , один из корней которого отделен , т.е. найден отрезок ( а , в ) , на концах которого значения функции f(x) имеют разные знаки . Для нахождения корня

Р е ш е н и е н е л и н е й н ы х у р а в н е н и й м е т о д о м х о р д
Метод хорд является более быстрым способом нахождения корня уравнения f (x)=0 , нежели метод половинного деления (Рис. 1). Пусть функция f(x) непрерывна на отрезке ( а , в

К а с а т е л ь н ы х
Метод касательных , называемый также методом Ньютона, широко используется при построении итерационных алгоритмов. Его попу-лярность объясняется быстрой сходимостью при хорошем начал

П р о с т ы х и т е р а ц и й
Этот метод решения уравнения f(х) = 0 состоит в замене исходного уравнения эквивалентным ему уравнением х = j(х) и построении последовательности хn+1 = j (хn)

Интерполяция зависимостей
Одной из важнейших задач процесса математического моделирования является вычисление значений функций, входящих в математическое описание модели. Для сложных моделей подобные вычисления могут б

Вычисление определенных интегралов методом Симпсона.
Для применения метода Симпсона промежуток интегрирования делится равноотстоящими ординатами на четное число частей.

CALL IDRES(X1,X2,EPS,X,K)
0

CALL KHORD (X1,X2,EPS,X,K)
CALL IDRES(X1,X2,EPS,X,K) 10 STOP END SUBROUTINE KHORD(A,B,EPS,X,K) * РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ * МЕТОДОМ ХОРД PRINT*,'ВВЕДИ

CALL NEWTO (X1,X2,EPS,X,K)
CALL IDRES(X1,X2,EPS,X,K) 10 STOP END SUBROUTINE NEWTO (A,B,EPS,X,K) * РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ * МЕТОДОМ НЬЮТОНA PRINT*,'В

CALL NEWTO (X1,X2,EPS,X,K)
CALL IDRES(X1,X2,EPS,X,K) 10 STOP END SUBROUTINE PRITE (A,B,EPS,X,K) * РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ * МЕТОДОМ ПРОСТЫХ ИТЕРАЦИЙ

PROGRAM U6
PRINT*,'ЧИСЛЕННОЕ ИНТЕГРИРОВAНИЕ МЕТОДОМ ТРAПЕЦИЙ' PRINT*,'ВВЕДИТЕ НИЖНИЙ И ВЕРХНИЙ ПРЕДЕЛ' PRINT*,'A ТAКЖЕ РAСЧЁТНОЕ КОЛИЧЕСТВО ОРДИНAТ' READ(5,*) A,B,N H=(B-A)