Логарифмические частотные характеристики типовых звеньев

Покажем технику построения ЛЧХ на примере двух динамических звеньев.

Безынерционное звено. Логарифмируя частотную передаточную функцию (4.15) , найдем

 

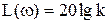(4.50)

 

Рис.4.17

Так как k от частоты не зависит, ЛАХ безынерционного звена представляет прямую, параллельную оси абсцисс (рис. 4.17).

 

Апериодическое звено. Заменив в (4.22) оператор р на jw после логарифмирования получим

 

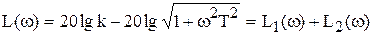, (4.51)

 

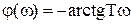. (4.52)

 

Рассмотрим вторую составляющую в (4.51)

 

(4.53)

 

В диапазоне частот, когда 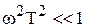, можно считать 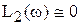. При частотах, когда получим 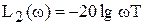. При подкоренное выражение равно 2 и 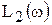=3 дб. Логарифмическая амплитудная характеристика в этом случае может быть представлена в виде двух прямых (асимптот), сопрягаемых в точке .

Рис. 4.19

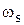Частота называется сопрягающей частотой. Асимптота 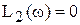совпадает с осью абсцисс, а асимптота 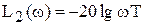наклонена к оси. Наклон второй асимптоты найдем по двум точкам: 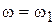и . Разность ординат составит

дб .

 

Это означает, что при двукратном изменении частоты прямая имеет наклон - 6 дб на октаву. При десятикратном изменении частоты раз­ность ординат

 

дб.

 

Наклон прямой при этом составит -20 дб/дек. Знак (-) показывает, что при возрастании частоты ординаты ЛАХ убывают (отрицательный наклон).

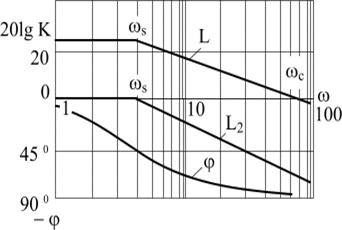На рис. 4.18 показано сопряжение двух асимптот. Первая асимптота параллельна оси абсцисс и отстоит от нее на расстоянии . Результирующая ЛАХ апериодического звена получается сложением двух составляющих. В окрестности сопряжение может быть произведено плавной кривой, проходящей через точку, лежащую ниже пересечения асимптот на 3 дб. Частота, при которой ЛАХ пересекает ось абсцисс, называется частотой среза.

Логарифмическая фазовая характеристика 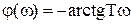может быть построена по точкам (рис.4.18). Характерными точками являются , .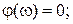

 

 

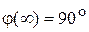ГЛАВА 5

 

МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ АВТОМАТИЧЕСКИХ СИСТЕМ

 

5.1. Общие замечания

 

Различают два рода уравнений автоматических систем: урав­нения статики (уравнения состояния равновесия) и уравнения динамики (уравнения переход­ных процессов).

Уравнения статики отражают связь между величинами, характеризующи­ми автоматическую систему в ее установившихся состояниях. По уравнениям статики определяются значения ре­гулируемых величин, положения регу­лирующих органов, расходы энергии или вещества через систему, параметры настройки и т. д.

Уравнения динамики описывают по­ведение автоматической системы в переходных процессах при появлении возмущающих сил, и после прекращения их действия.

Все автоматические системы состоят из элементов, которые можно разделить на два типа: элементы с сосредоточенными параметрами, элементы с распределенными параметрами.

Элементы с сосредоточенными параметрами. Физическое состояние таких эле­ментов и их поведение в системе полностью определяется конечным числом переменных. Эти переменные могут иметь любую физи­ческую природу (температура, давле­ние, скорость, напряжение и т. д.). Переменные величины, задающие состояние элемента, носят название “обобщенных координат” этого элемен­та. Число обобщенных ко­ординат определяет число степеней свободы элемента с сосредоточенными параметрами. Примером элемента с сосредоточенными параметрами может служить физический маятник, состоя­ние которого при заданной длине оп­ределяется одной координатой - от­клонением центра тяжести маятника от положения равновесия. Динамика элементов с сосредоточенными параметрами описывается обыкновенными диффе­ренциальными уравнениями.

Элементы с распределенными параметрами. Элементы этого типа имеют бесконечное число степеней сво­боды. Примером таких элементов может служить линия электропередачи, стенка трубы парового котла и т.д. Динамика элементов с распределенными параметрами описывается дифференциальными уравнениями в частных производных.

С точки зрения математического описания, простейшими динамическими систе­мами являются системы с одной сте­пенью свободы. Однако необходимо отметить, что число степеней свободы не всегда предопределяет степень тех­нической сложности элемента или системы. Напри­мер, такой конструктивно сложный ме­ханизм, как двигатель внутреннего сгорания в задаче регулирования его числа оборотов обычно рассматривает­ся как система с одной степенью свобо­ды, то есть как простейшая динамическая система; в то же время шарик, свобод­но катящийся по горизонтальной плос­кости, представляет собой систему с пятью степенями свободы.

Если система автоматического регулиро­вания состоит из элементов с сосредоточенными параметра­ми, то при математическом описании она расчленяется на звенья с одной степенью свободы. Число таких звеньев будет равно числу степеней свободы расчленяемой системы или числу переменных участвующих в данной модели.