Интегральные преобразования Лапласа
В исследовании динамики автоматических систем широко применяются интегральные преобразования Лапласа, Хевисайда-Карсона, Фурье. Одна из привлекательных сторон этих преобразований в том, что они понижают сложность математических операций. Например, обыкновенные дифференциальные уравнения после интегрального преобразования превращаются в алгебраические, а уравнения в частных производных - в более простые, обыкновенные дифференциальные уравнения. Так как преобразование Лапласа является одним из основных математических инструментов теории автоматического управления, рассмотрим основные правила работы с ним.
Суть преобразования состоит в том, что для функции времени 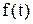 конструируется специальная функция новой переменной
конструируется специальная функция новой переменной 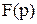 более простая, чем исходная. Функцию
более простая, чем исходная. Функцию 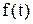 называют “оригинал”, а
называют “оригинал”, а 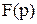 – “изображение”. Соответствие между ними обозначают так
– “изображение”. Соответствие между ними обозначают так
 (1.5)
(1.5)
Аналитическая связь между оригиналом и изображением устанавливается посредством прямого и обратного преобразований.
Прямое преобразование Лапласа определяет переход от функции 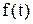 к функции
к функции 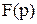 , который осуществляется по формуле
, который осуществляется по формуле
 (1.6)
(1.6)
Приведем без доказательства примеры прямых преобразований над несколькими часто используемыми функциями времени.
1. Если  , где A – постоянная величина, то изображением этой функции будет
, где A – постоянная величина, то изображением этой функции будет
 (1.7)
(1.7)
2. Если оригиналом выступают производные 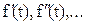 , то их изображения определяются так
, то их изображения определяются так
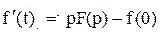
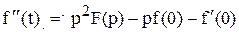 (1.8)
(1.8)
…

где f(0),  ,…– начальные значения функции и ее производных. Этим преобразованием дифференцирование заменяется на более простую операцию - умножение.
,…– начальные значения функции и ее производных. Этим преобразованием дифференцирование заменяется на более простую операцию - умножение.
3. Изображение интеграла от 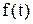 представляется следующим образом
представляется следующим образом
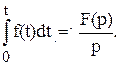 (1.9)
(1.9)
Как отсюда видно этим преобразованием операция интегрирования заменяется на операцию деления.
Обратное преобразование Лапласа осуществляет обратный переход от функции 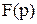 к функции
к функции 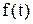 . Этот переход может быть сделан несколькими путями.
. Этот переход может быть сделан несколькими путями.
Первый путь состоит в применении так называемых “формул соответствия” между F(p) и 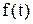 , которые публикуются в специальных справочниках.
, которые публикуются в специальных справочниках.
Второй путь это проведение обратного преобразования с использованием математического аппарата теории вычетов.
Третий путь считается основным и состоит в применении так называемых “формул разложения”, на правилах использования которых остановимся подробнее.
Формулы разложения применимы для изображений, которые можно представить в виде дроби числитель и знаменатель которой являются полиномами
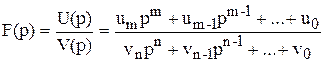 (1.10)
(1.10)
при условии, что 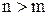 .
.
В теории преобразований Лапласа получены две формулы разложения, область использования которых определяется корнями полинома  .
.
Если среди корней этого полинома p1, p2,…, pn нет кратных, то оригинал определяется по формуле
 (1.11)
(1.11)
Если в уравнении  есть кратные корни, то должна использоваться другая формула
есть кратные корни, то должна использоваться другая формула
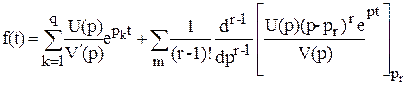 (1.12)
(1.12)
Эта формула написана для полинома имеющего q простых корней (p1, p2,…, pq) и m кратных корней, один из которых имеет кратность r.
Примечание. Практическая работа с формулами разложения приводит к двум алгебраическим задачам.
Первая задача - это нахождение корней  . Эта задача может представлять серьезную самостоятельную проблему при работе с полиномами больших степеней. В специальной технической и математической литературе описываются различные аналитические и графические методы определения корней.
. Эта задача может представлять серьезную самостоятельную проблему при работе с полиномами больших степеней. В специальной технической и математической литературе описываются различные аналитические и графические методы определения корней.
Вторая задача возникает, когда среди корней  есть комплексные, и оригинал, полученный в комплексной форме, приходится преобразовывать в вещественную форму.
есть комплексные, и оригинал, полученный в комплексной форме, приходится преобразовывать в вещественную форму.
Пусть среди корней V(p) есть комплексные корни 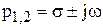 . Их подстановка в формулу разложения даст оригинал тоже в комплексной форме
. Их подстановка в формулу разложения даст оригинал тоже в комплексной форме
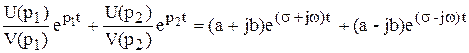
Для перехода к вещественной форме записи поступают так. Записывают
 и
и 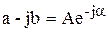 , где
, где 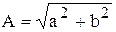 ,
, 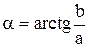 , и по формуле Эйлера находят
, и по формуле Эйлера находят
 .
.
Теперь оригинал будет записан в вещественной форме следующим образом
.
Некоторые теоремы и предельные соотношения.1. Теорема запаздывания (теорема о смещении в области оригиналов). Если функции f(t) соответствует изображение F(p) , то функции  будет соответствовать изображение
будет соответствовать изображение 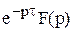 . Для доказательства введем новую переменную
. Для доказательства введем новую переменную  , и учтем, что
, и учтем, что 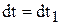 и
и 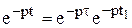
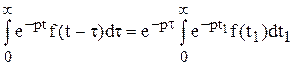 .
.
2. Теорема смещения в области изображений. Если изображению F(p) соответствует f (t), то изображению 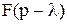 соответствует функция
соответствует функция 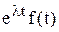 . Действительно
. Действительно
 .
.
3. Теорема о предельном переходе. Определяет формулу нахождения начального значения функции f(0) по изображению, без применения обратного преобразования
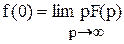 .
.
Пример 1.3. Записать интегральное преобразование Лапласа для дифференциального уравнения
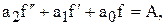
где A – постоянная величина,  и
и  – начальные условия.
– начальные условия.
Решение. Запишем изображения всех составляющих исходного уравнения, то есть изображения функции, ее производных и правой части:
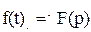 ,
, 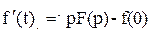 ,
, 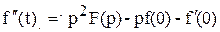 .
.
Так как правая часть уравнения постоянная величина, то ее изображением будет


После подстановки всех изображений в исходное уравнение получим операторное уравнение
 .
.
Решением этого уравнения является функция

где 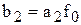 ,
, 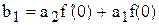 ,
, 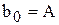 .
.
Пример 1.4.Найти оригинал для изображения 
Решение. Полином 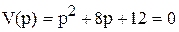 имеет корни
имеет корни  ,
, 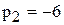 . И так как эти корни не кратные оригинал определяем по формуле разложения (1.11). Учитывая, что
. И так как эти корни не кратные оригинал определяем по формуле разложения (1.11). Учитывая, что 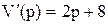 , оригинал будет такой
, оригинал будет такой

Пример 1.5.Найти оригинал для 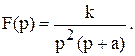
Решение. Среди корней  корень
корень 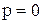 второй кратности, поэтому оригинал определяется по формуле разложения (1.12). Корню
второй кратности, поэтому оригинал определяется по формуле разложения (1.12). Корню 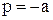 соответствует оригинал
соответствует оригинал
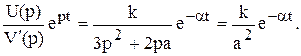
Корню 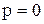 соответствует оригинал
соответствует оригинал
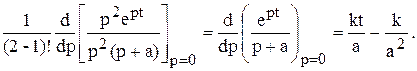
Следовательно,
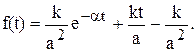
ГЛАВА 2
СТРУКТУРНЫЕ СХЕМЫ И ИХ ПРЕОБРАЗОВАНИЯ
2.1. Понятие о структурной схеме
Пусть между переменными x1 и x2 установлено линейное преобразование
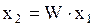 . (2.1)
. (2.1)
Введем понятие “звена”, которому присвоим свойство производить преобразование W над входным сигналом x1. Изобразим это звено в виде прямоугольника, и укажем направление действия сигнала стрелками. Тогда преобразованию в алгебраической форме (2.1) будет соответствовать схема, изображенная на рис. 2.1.

Рис. 2.1
Если в преобразовании участвует более двух переменных, то графическим изображением такого преобразования уже будет схема с несколькими звеньями, соединенными между собой связями. Для того, чтобы схема была эквивалентна своей алгебраической форме, на звено и связи должны быть наложены следующие условия: 1) звено обладает детекторным эффектом, то есть сигнал в звене проходит только в одном направлении: от входа к выходу;
2) при разветвлении сигнала в узле он не делится.
Схемы, составленные из таких звеньев, называются структурными схемами. При изображении структурных схем придерживаются следующих условных обозначений: внутри прямоугольника, определяющего звено, указывается его функция преобразования; соединения звеньев показываются линиями со стрелками, показывающими направления действия сигналов; в месте разветвления сигнала ставится точка (рис.2.2, а); суммирование сигналов обозначается кружком с указанием знака операции (рис.2.2, б); узел сравнения обозначается кружком с перекрещенными линиями (рис.2.2, в).
 |

Рис. 2.2
 На приведенном ниже примере читатель может убедиться в эквивалентности системы уравнений и изображенной рядом структурной схемы.
На приведенном ниже примере читатель может убедиться в эквивалентности системы уравнений и изображенной рядом структурной схемы.
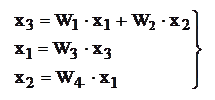
Решить систему уравнений относительно двух переменных, например, относительно 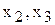 , где
, где  зависимая переменная, это значит найти зависимость
зависимая переменная, это значит найти зависимость  , в которой исключены все остальные переменные. Получить это же решение на структурной схеме, это значит преобразовать схему в эквивалентное звено, входом и выходом которого должны быть точки действия соответствующих переменных, в данном случае это
, в которой исключены все остальные переменные. Получить это же решение на структурной схеме, это значит преобразовать схему в эквивалентное звено, входом и выходом которого должны быть точки действия соответствующих переменных, в данном случае это 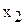 и
и  . При этом входом схемы служит независимая переменная
. При этом входом схемы служит независимая переменная 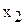 , а выходом зависимая переменная
, а выходом зависимая переменная  .
.
Вывод. Структурная схема является одним из методов записи и решения систем линейных алгебраических уравнений. Решение системы превращается в процедуру преобразования структурной схемы в эквивалентное звено.
2.2. Правила преобразования структурных схем
Приведенные ниже правила показывают основные, типовые преобразования простейших схем в эквивалентное звено и определяют формулы для определения передаточной функции этого звена. Правила иллюстрируются на примерах соединения (2-3) звеньев.
Последовательное соединение звеньев (рис.2.3). Такому соединению звеньев эквивалентна следующая система уравнений
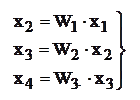
 |
Рис. 2.3
Подстановка первого уравнения во второе, а второго в третье дает решение системы уравнений и значение передаточной функции эквивалентного звена
 .
.
В общем случае при последовательном соединении n звеньев их передаточные функции перемножаются
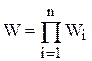 . (2.2)
. (2.2)
Параллельное соединение звеньев (рис.2.4). При параллельном соединении на входах звеньев действует единый сигнал, а выходные сигналы складываются (или вычитаются). Это равносильно следующей системе уравнений
 |
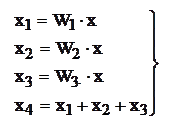
|
|
Подставляя первые три уравнения системы в четвертое, получим
 .
.
При параллельном соединении n звеньев их передаточные функции складываются
 . (2.3)
. (2.3)
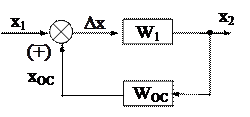
Схема с обратной связью (рис.2.5). В схемах этого типа сигнал с выхода схемы подается на ее вход со знаком (-) или (+), преобразуясь предварительно в звене обратной связи. Такой схеме соответствует следующая система алгебраических уравнений
 |
|

После исключения переменных 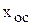 и Dх получим решение системы и значение эквивалентной передаточной функции
и Dх получим решение системы и значение эквивалентной передаточной функции
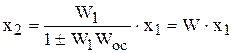 . (2.4)
. (2.4)
В этой формуле знак (+) соответствует отрицательной обратной связи, а знак (-) положительной.
Перенос точки разветвления через звено. В исходной схеме (рис.2.6, а) точка разветвления может быть перенесена как по ходу сигнала, так и против хода.
При переносе точки по ходу сигнала (рис. 2.6,б) в цепь ответвления сигнала ставится звено с передаточной функцией 1/W2 , в результате чего сигнал восстанавливается от лишнего преобразования W2.

При переносе точки разветвления против хода сигнала (рис. 2.6,в) в цепь ответвления ставится звено, эквивалентное тому, через которое точка переносится. При этом сигнал при переносе не теряет преобразование W1 .
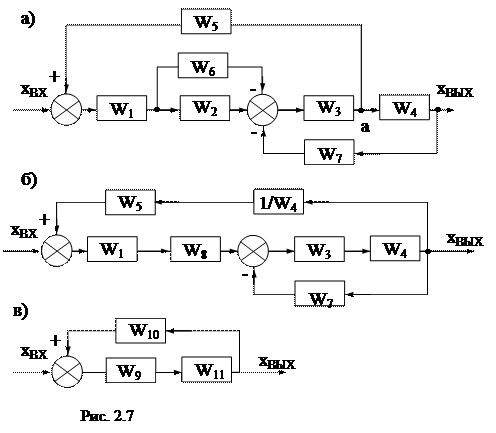 Пример 2.1. Для структурной схемы изображенной на рис. 2.7,а найти передаточную функцию относительно точек
Пример 2.1. Для структурной схемы изображенной на рис. 2.7,а найти передаточную функцию относительно точек 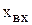 ,
,  . Последовательность упрощений исходной схемы показана на рис. 2.7,б,в.
. Последовательность упрощений исходной схемы показана на рис. 2.7,б,в.  Звенья W2,W6 соединены параллельно, и поэтому запишем
Звенья W2,W6 соединены параллельно, и поэтому запишем  . Преобразованию группы звеньев W3,W4,W7 мешает точка съема сигнала а, поэтому переносим ее по ходу сигнала через звено W4. Схема, полученная после этих преобразований, приведена на рис. 2.7,б. Далее преобразуем две группы последовательно соединенных звеньев W9 = W1W8, W10 = W5 + 1/W4 и цепь с отрицательной обратной связью W11=W3W4/ (1+W3 W4W7).
. Преобразованию группы звеньев W3,W4,W7 мешает точка съема сигнала а, поэтому переносим ее по ходу сигнала через звено W4. Схема, полученная после этих преобразований, приведена на рис. 2.7,б. Далее преобразуем две группы последовательно соединенных звеньев W9 = W1W8, W10 = W5 + 1/W4 и цепь с отрицательной обратной связью W11=W3W4/ (1+W3 W4W7).
В результате получена схема изображенная на рис. 2.7,в, представляющая собой контур с положительной ОС. Преобразование этого контура дает следующую передаточную функцию
 .
.
После соответствующих подстановок и преобразований окончательно получим
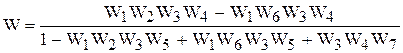 . (2.5)
. (2.5)
Во многих практических расчетах структурные схемы настолько сложные, что пользоваться методом последовательных преобразований становится неудобно, и в этих случаях используют универсальную формулу Мейсона. По формуле Мейсона передаточная функция относительно точек c-вход и d-выход определяется так
 . (2.6)
. (2.6)
Здесь m – количество прямых путей от c к d , а  - передаточная функция i-го прямого пути; k – количество независимых замкнутых контуров схемы, а
- передаточная функция i-го прямого пути; k – количество независимых замкнутых контуров схемы, а  - передаточная функция j-го контура; знаком «
- передаточная функция j-го контура; знаком «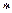 » обозначено исключение в числителе и знаменателе всех слагаемых в которых встречаются произведения передаточных функций одних и тех же звеньев (включая звенья с передаточной функцией, равной единице).
» обозначено исключение в числителе и знаменателе всех слагаемых в которых встречаются произведения передаточных функций одних и тех же звеньев (включая звенья с передаточной функцией, равной единице).
Пример 2.2. Найти по формуле Мейсона передаточную функцию структурной схемы предыдущего примера (рис. 2.7,а).
Решение. Схема имеет два прямых пути (n=2) это W1W2W3W4 и W1W6 (-1)W3W4; три замкнутых контура (m=3) W1W2W3W5 , W1W6(-1)W3W5 , W3W4W7(-1). Подставив эти значения в формулу (2.6), получим
 ,
,
где 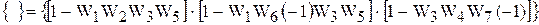 .
.
После раскрытия скобок и исключения всех слагаемых, содержащих произведения одинаковых передаточных функций, получим выражение
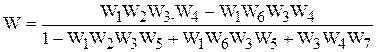 ,
,
совпадающее с выражением (2.5), полученным ранее путем последовательных структурных преобразований.
2.4. Передаточные функции структурной схемы
 Структурная схема может иметь столько передаточных функций, сколько отличающихся пар точек в ней можно указать. При этом в каждой паре точек одна считается входом (с), а другая выходом (d). О такой передаточной функции будем говорить, что она составлена относительно точек (с,d), и отмечать это индексами
Структурная схема может иметь столько передаточных функций, сколько отличающихся пар точек в ней можно указать. При этом в каждой паре точек одна считается входом (с), а другая выходом (d). О такой передаточной функции будем говорить, что она составлена относительно точек (с,d), и отмечать это индексами
 .
.
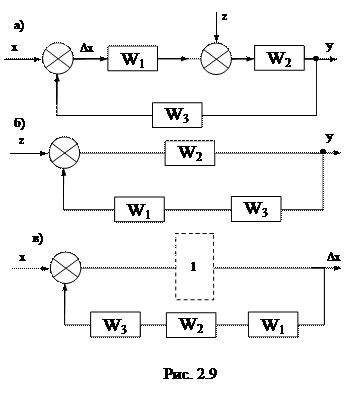
На рис.2.9 изображена структурная схема, в которой действует три внешних воздействия: задающее - x, возмущающее – z и выходное - y , а за элементом сравнения действует рассогласование (ошибка) 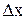 . Ряд преобразований этой схемы, показанных ниже, позволит нам сформулировать несколько полезных правил, существенно упрощающих работу со структурными схемами.
. Ряд преобразований этой схемы, показанных ниже, позволит нам сформулировать несколько полезных правил, существенно упрощающих работу со структурными схемами.
| |



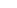
 Преобразование 1. Определим реакцию системы на задающее воздействие х. Считаем
Преобразование 1. Определим реакцию системы на задающее воздействие х. Считаем 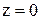 и в схеме (рис. 2.9,а) принимаем за вход и выход соответственно точки x и y. Передаточная функция относительно этих точек будет следующей
и в схеме (рис. 2.9,а) принимаем за вход и выход соответственно точки x и y. Передаточная функция относительно этих точек будет следующей
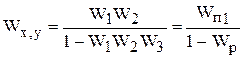 , (2.8)
, (2.8)
где  - передаточная функция прямого пути, а
- передаточная функция прямого пути, а  - передаточная функция разомкнутой структурной схемы.
- передаточная функция разомкнутой структурной схемы.
Реакция системы на воздействие х определится уравнением
 . (2.9)
. (2.9)
Преобразование 2. Определим реакцию системы на возмущающее воздействие z. Теперь считаем  , а за вход и выход принимаются соответственно точки z и y (рис. 2.9,б). Передаточная функция в этом случае равна
, а за вход и выход принимаются соответственно точки z и y (рис. 2.9,б). Передаточная функция в этом случае равна
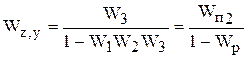
где 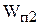 - передаточная функция прямого пути. Реакция системы на воздействие z
- передаточная функция прямого пути. Реакция системы на воздействие z
 . (2.11)
. (2.11)
В силу линейного характера структурной схемы полную реакцию системы определим наложением двух режимов, то есть
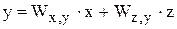 .
.
Анализ (2.8) и (2.9) иллюстрирует характерное свойство передаточных функций. Передаточная функция относительно двух произвольных точек «c,d» представляется дробью, в числителе которой записывается передаточная функция разомкнутого участка между выбранными точками, а в выражении знаменателя используется передаточная функция разомкнутой системы в выражении 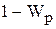 . Это можно записать так
. Это можно записать так
 .
.
Воспользуемся этим правилом для определения ошибки 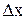 , вызванной действием задания x. Для этого достаточно найти передаточную функцию исходной схемы (рис. 2.8,а) относительно точек
, вызванной действием задания x. Для этого достаточно найти передаточную функцию исходной схемы (рис. 2.8,а) относительно точек 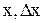 . Так как передаточная функция прямого пути от x к
. Так как передаточная функция прямого пути от x к 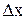 равна единице (рис. 2.8,в), то передаточная функция по ошибке будет равна
равна единице (рис. 2.8,в), то передаточная функция по ошибке будет равна
 ,
,
а сама ошибка будет равна
 .
.
ГЛАВА 3