Порядок виконання роботи
1. Сутність лінійної дискретної обробки
2. Зв'язок АЧХ з розташуванням нулів і полюсів
3. Всепропускающіе фільтри
4. Фільтри першого порядку
9.1. Короткі теоретичні відомості та методичні вказівки
У літературі «дискретна система» і «дискретний фільтр» - це одне і те ж, однак поняття «фільтр», свідомо чи підсвідомо, досить тісно пов'язується з системами, які одні частоти пропускають, а інші затримують. Такий підхід може створити помилкове, обмежене уявлення про призначення та можливості дискретних лінійних систем, які здатні виконувати й інші завдання, ніж виділення з сигналу певної смуги частот. У тексті слова «фільтр» і «система» будуть використовуватися як синоніми.
9.2. Сутність лінійної дискретної обробки
Взагалі, дискретний фільтр - це довільна система обробки дискретного сигналу, що має властивості лінійності і стаціонарності. Під цими властивостями розуміється те ж, що і в аналоговому разі: лінійність означає, що вихідна реакція на суму сигналів дорівнює сумі реакцій на ці сигнали, подані на вхід окремо, а стаціонарність - що затримка вхідного сигналу призводить лише до такої ж затримки вихідного сигналу, не змінюючи його форми.
Будь-який фільтр має певної частотною характеристикою. Щоб вона була нетривіальною, тобто щоб коефіцієнт передачі фільтра на різних частотах був різним, вихідний сигнал фільтра y(k)) має залежати від декількох відліків вхідного сигналу x(k). Таким чином, дискретний фільтр повинен володіти пам'яттю.
Щоб забезпечити лінійність і стаціонарність, вироблені фільтром математичні операції повинні обмежуватися складанням і множенням на константи.
Розглянемо найпростіший приклад. Нехай вихідний сигнал фільтра дорівнює сумі двох останніх відліків вхідного сигналу:
y(k) =x(k) + x(k - 1).
Переконаємося в тому, що ця система по-різному пропускає на вихід сигнали різних частот. Для початку подамо на вхід фільтру серію однакових відліків (тобто сигнал нульової частоти):
Таблиця 9.1
| Вхід | Вихід |
| ... | ... |
| ... | |
| 1 + 1=2 | |
| 1 + 1=2 | |
| 1 + 1=2 | |
| ... | ... |
Рівень постійного сигналу фільтр збільшив у два рази. Тепер подамо на вхід відліки, однакові по модулю, але з чергуються знаками (тобто відліки гармонійного сигналу з частотою Найквіста):
Таблиця 9.2
| Вхід | Вихід |
| ... | ... |
| ... | |
| -1 | -1 + 1 = 0 |
| 1 +(-1) = 0 | |
| -1 | -1 + 1= 0 |
| ... | ... |
На відміну від постійного сигналу, сигнал з частотою Найквіста на вихід просто не пройшов. Далі спробуємо що-небудь проміжне, наприклад сигнал з частотою, яка дорівнює половині частоти Найквіста:
Таблиця 9.3
| Вхід | Вихід |
| ... | |
| 0+1 = 1 | |
| -1 | -1 + 0 = 1 |
| 0 + (-1) = - 1 | |
| 1+0=1 | |
| 0 + 1 = 1 | |
| -1 | -1 + 0 = - 1 |
На виході в даному випадку виходять відліки синусоїди, що має в 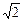 разів більшу амплітуду і деяке фазове зрушення в порівнянні з вхідним сигналом. Розглянутий приклад являє собою найпростіший випадок нерекурсивного фільтра. Такі фільтри підсумовують деяке число вхідних відліків, примножуючи їх при цьому на постійні вагові коефіцієнти. Тепер зауважимо, що крім вхідних відліків ми можемо використовувати для обчислень і раніше розраховані значення вихідного сигналу. Спробуємо просто скласти докупи вхідний відлік і попередній вихідний відлік: y(k)= x(k) + y(k-1).Подаємо на вхід постійний сигнал (початковий стан фільтра вважаємо нульовим):
разів більшу амплітуду і деяке фазове зрушення в порівнянні з вхідним сигналом. Розглянутий приклад являє собою найпростіший випадок нерекурсивного фільтра. Такі фільтри підсумовують деяке число вхідних відліків, примножуючи їх при цьому на постійні вагові коефіцієнти. Тепер зауважимо, що крім вхідних відліків ми можемо використовувати для обчислень і раніше розраховані значення вихідного сигналу. Спробуємо просто скласти докупи вхідний відлік і попередній вихідний відлік: y(k)= x(k) + y(k-1).Подаємо на вхід постійний сигнал (початковий стан фільтра вважаємо нульовим):
Таблиця 9.4
| Вхід | Вихід |
| 1 + 0 = 1 | |
| 1 + 1 = 2 | |
| 1 + 2 = 3 | |
| 1 + 3 = 4 | |
| ... | ... |
Так, очевидно, буде продовжуватися і далі - вихідний сигнал буде лінійно наростати, що рано чи пізно призведе до переповнення розрядної сітки обчислювального пристрою. Це відразу ж демонструє нам головну відмінну рису фільтрів, що використовують при обчисленнях попередні відліки вихідного сигналу (їх називають рекурсивними фільтрами) - через наявність зворотних зв'язків вони можуть бути нестійкими.
Спробуємо зменшити вплив зворотного зв'язку, розділивши попередній відлік вихідного сигналу на 2: y(k) = x(k) + 0,5 y(k - 1).
Знову подаємо на вхід постійний сигнал:
Таблиця 9.5
| Вхід | Вихід |
| 1 +0,5*0 = 1 | |
| 1 + 0,5*1 = 1,5 | |
| 1 + 0,5*1,5 = 1,75 | |
| 1 + 0,5*1,75 = 1,875 | |
| 1 +0,5*1,875 = 1,9375 | |
| … | … |
Як бачимо, ситуація радикально змінилася - тепер вихідний сигнал з зменшується швидкістю прагне до значення 2. Таким чином, перехідний процес в фільтрі є нескінченним. Це ще одна відмітна риса рекурсивних фільтрів.
Отже, рекурсивні фільтри підсумовують при розрахунках не тільки вхідні, але і деяка кількість попередніх вихідних відліків сигналу, примножуючи їх при цьому на постійні вагові коефіцієнти.
У загальному випадку дискретний фільтр підсумовує (з ваговими коефіцієнтами) деяка кількість вхідних відліків (включаючи останній) і деяку кількість попередніх вихідних відліків:
y(k) = b0 x(k) + b1 x(k - 1) + ... + bm x(k - m) -
- a1 y(k - 1) - a2 y(k - 2) - ... - an y(k - n),
де aj і bi — речові коефіцієнти.
Дана формула називається алгоритмом дискретної фільтрації. Якщо по-іншому згрупувати доданки, щоб з одного боку від знаку рівності були тільки вхідні відліки, а з іншого - лише вихідні, отримаємо форму запису, звану різницевим рівнянням:
y(k) + a1 y(k - 1) + a2 y(k - 2) + ... + an y(k - n)=
= bo x(k) + b1 x(k - 1) + ... + bm x(k - m).
Структура різницевого рівняння схожа на структуру диференціального рівняння аналогової лінійної системи, тільки замість операції диференціювання у формулі фігурують затримки дискретних послідовностей. Цим визначається спільність підходів до опису аналогових і дискретних систем. Однак досить істотним є те, що в дискретній системі не існує будь-яких принципових обмежень на співвідношення між m і n - кількостями вхідних і вихідних відліків, що використовуються при обчисленнях.
9.3. Зв'язок АЧХ з розташуванням нулів і полюсів
Відмінність від аналогового випадку полягає в тому, що при розрахунку частотної характеристики точка, яка зображує аргумент функції передачі на комплексній площині, рухається не вздовж уявної осі, а по одиничному колі. Це дозволяє зробити наступні висновки:
- Якщо нуль лежить на одиничному колі, АЧХ на відповідній частоті буде мати нульове значення.
- Якщо полюс лежить на одиничному колі, АЧХ на відповідній частоті буде прагнути до нескінченності.
- Чим ближче до одиничної окружності розташований нуль (полюс), тим більш вираженим буде відповідний провал (підйом) АЧХ.
В якості прикладу розглянемо систему, котра має пару полюсів, рівних 0,2 ± 0,9j і чотири нулі, два з яких (0,8 ± 0,6j) розташовані на одиничному колі, а ще два (-0,8 ± 0,8j) - поблизу неї.
function Example9_1
z=[0.8+0.6i -0.8+0.8i]'; % нулі функції передачі (стовпець)
z=[z; conj(z)]; % створюємо комплексно-зв'язані пари
p=0.2+0.9i; p=[p; conj(p)]; % полюси функції передачі (стовпець)
k=1; % загальний коефіцієнт посилення
[b,a]=zp2tf(z, p, k); % пошук функції передачі
[h,f]=freqz(b, a); % розрахунок коефіцієнта передачі
plot(f/pi,abs(h)) % графік АЧХ
grid on % На екрані АЧХ ланцюга підтверджує передбачення, зроблені виходячи з розташування нулів і полюсів
9.4. Всепропускающіе фільтри
Всепропускающімі (allpass) називають фільтри, АЧХ яких дорівнює одиниці на всіх частотах. Умови, при яких фільтр є всепропускающім:
□ кількість нулів дорівнює числу полюсів;
□ □ значення нулів є зворотними і комплексно-спряженими по відношенню до полюсів;
□ коефіцієнт посилення k дорівнює добутку модулів полюсів фільтра.
function Example9_2
p=[0.5+0.5i; 0.5-0.5i; -0.7]; % полюси фільтра
z=1./conj(p); % нулі фільтра
k=prod(abs(p)); % коефіцієнт посилення
[b, a]=zp2tf(z, p, k); % функція передачі
freqz(b, a) % частотні характеристики
На екрані АЧХ і ФЧХ всепропускающего фільтра
9.5. Фільтри першого порядку
Для отримання частотних характеристик ФНЧ використаний наступний код MATLAB:
function Example9_3
b=[1 1]; % чисельник функції передачі
p=[-0.5 0 0.5 0.7 0.9]; % вектор значень параметра р
hold off
for k=1:length(p) % цикл за значенням р
a=[1 -p(k)]; % знаменник функції передачі
k0=(1-p(k))/2; % постійний множник
[h(:,k),f]=freqz(b*k0, a); % розрахунок частотної характеристики
plot(f/pi, abs(h(:,k))) % графік АЧХ
hold on
end
hold off
grid on
xlabel('Normalized friquency')
На екрані АЧХ при різних значеннях параметра для ФНЧ. Параметр р регулює смугу пропускання.
Для отримання частотних характеристик ФВЧ використаний наступний код MATLAB:
function Example9_4
b=[1 -1]; % чисельник функції передачі
p=[-0.5 0 0.5 0.7 0.9]; % вектор значень параметра р
hold off
for k=1:length(p) % цикл за значенням р
a=[1 p(k)]; % знаменник функції передачі
k0=(1-p(k))/2; % постійний множник
[h(:,k),f]=freqz(b*k0, a); % розрахунок частотної характеристики
plot(f/pi, abs(h(:,k))) % графік АЧХ
hold on
end
hold off
grid on
xlabel('Normalized friquency') % На екрані АЧХ при різних значеннях параметра для ФВЧ.
Питання для самоперевірки
1. У чому сутність лінійної дискретної обробки?
2. Який зв'язок АЧХ з розташуванням нулів і полюсів?
3. Що таке всепропускающіе фільтри?
4. Що таке фільтри першого порядку