Порядок виконання роботи
1. Зв'язок ДПФ і спектру дискретного аналізу.
2. Взаємозв'язок ДПФ і фільтрації.
3. Дискретна фільтрація за допомогою ДПФ.
11.1. Короткі теоретичні відомості та методичні вказівки
При дискретизації аналогового сигналу його спектр стає періодичним з періодом повторення, рівним частоті дискретизації. Проте одного тільки цього співвідношення виявляється недостатньо для вирішення всіх практичних задач спектрального аналізу. По-перше, в якості вихідних даних виступає саме послідовність дискретних відліків, а не аналоговий сигнал. По-друге, в більшості випадків аналізовані сигнали є випадковими процесами, що вимагає виконання будь-якого усереднення при розрахунку їх спектрів. Крім того, в ряді випадків нам відома деяка додаткова інформація про аналізованому сигналі, і цю інформацію бажано врахувати в спектральному аналізі.
Перш за все розглянемо дискретне перетворення Фур'є (ДПФ) - різновид перетворення Фур'є, спеціально призначену для роботи з дискретними сигналами. Далі обговоримо ідеї, що лежать в основі алгоритмів швидкого перетворення Фур'є, що дозволяють значно прискорити обчислення.
Дискретне перетворення Фур'є, по можливості обчислюване швидкими методами, лежить в основі різних технологій спектрального аналізу, призначених для дослідження випадкових процесів. Справа в тому, що якщо аналізований сигнал являє собою випадковий процес, то просте обчислення його ДПФ зазвичай не представляє великого інтересу, тому що в результаті виходить лише спектр єдиною реалізації процесу. Тому для спектрального аналізу випадкових сигналів необхідно використовувати усереднення спектру. Такі методи, в яких використовується лише інформація, що витягує з самого вхідного сигналу, називаються непараметрическими (nonparametric).
Інший клас методів припускає наявність деякої статистичної моделі випадкового сигналу. Процес спектрального аналізу в даному випадку включає в себе визначення параметрів цієї моделі, і тому такі методи називаються параметричними (parametric). Використовується також термін «модельний спектральний аналіз » (Model-Based Spectrum Analysis, MBSA).
11.2. Зв'язок ДПФ і спектру дискретного аналізу
Маючи один і той же кінцевий набір чисел, можна розрахувати або спектральну функцію цього дискретного сигналу
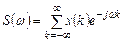,(11.1)
або його ДПФ
(11.2)
Виникає питання як пов'язані один з одним ці два спектральних уявлення, отримані на основі одних і тих же відліків сигналу.
Порівняння формул (11.1) і (11.2) показує, що ДПФ є просто дискретні відліки спектральної функції дискретного сигналу, відповідні частотам wn = wдn/N:
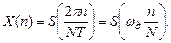(11.3)
Тому значення ДПФ іноді називають спектральними відліками. Зі співвідношення (11.3) випливає ще один важливий висновок: якщо додати до кінцевого набору відліків деяку кількість нулів, спектральна функція дискретного сигналу не зміниться, але ДПФ дасть більше число спектральних відліків, відповідних частотам, більш тісно розташованим в інтервалі від нуля до частоти дискретизації. Пояснимо сказане на простому прикладі, обчисливши ДПФ для відліків прямокутного імпульсу при різній кількості кінцевих нулів:
function Example11_1
x1=[ones(8,1); zeros(8,1)]; % 16 відліків
y1=fft(x1); % ДПФ сигналу х1
x2=[x1; zeros(16,1)]; % додаємо 16 нулів
y2=fft(x2); % ДПФ сигналу х2
subplot(2, 2, 1)
stem(0:15, x1) % графік сигналу х1
xlim([0 31])
subplot(2, 2, 2)
stem((0:15)/16, abs(y1)) % модуль ДПФ сигналу х1
subplot(2, 2, 3)
stem(0:31, x2) % графік сигналу х2
xlim([0 31])
subplot(2, 2, 4)
stem((0:31)/32, abs(y2)) % модуль ДПФ сигнала х2
На екрані показано підвищення спектрального дозволу ДПФ при доповненні сигналу нулями. Горизонтальні осі на спектральних графіках переписани в частках частоти дискретизації. Після збільшення довжини сигналу вдвічі за рахунок додавання нульових відліків результат ДПФ став містити вдвічі більше значень, що відповідають в два рази частіше розташованим частотах. Таким чином, доповнення сигналу нулями дозволяє підвищити спектральний дозвіл при обчисленні ДПФ.
11.3. Взаємозв'язок ДПФ і фільтрації
Розглянувши принципи дискретної фільтрації і познайомившись з дискретним перетворенням Фур'є, можна помітити, що формули, що описують ці два процеси, дуже схожі - в обох випадках вони представляють собою лінійну комбінацію відліків вхідного сигналу. Це говорить про те, що ДПФ можна трактувати як обробку сигналу фільтром з відповідною імпульсною характеристикою. імпульсну характеристику можна одержати, якщо зауважити, що ej2pn = 1 при целочисленном n, і з урахуванням цього перетворити формулу ДПФ (11.2) у вигляді
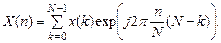
Для показу графіка АЧХ одного з каналів ДПФ при N = 8 потрібно виконати наступний набір команд:
function Example11_2
N=8;
w=0:0.1:N;
plot(w, abs(diric((w-3)/N*2*pi, N)))
hold on
plot(w, abs(diric((w-4)/N*2*pi, N)), '--')
hold off %
На екрані градуювання частотної осі виконана в номерах каналів. Пунктирною лінією зображено АЧХ сусіднього частотного каналу.
11.4. Дискретна фільтрація за допомогою ДПФ
Спочатку ставимо вхідні послідовності
>> x1=[1 2 4 8];
>> x2=[2 3 4 5];
Далі обчислюємо лінійну та кругову згортки (рис. 11.1 і 11.2), щоб потім було з чим порівняти результати фільтрації за допомогою ДПФ
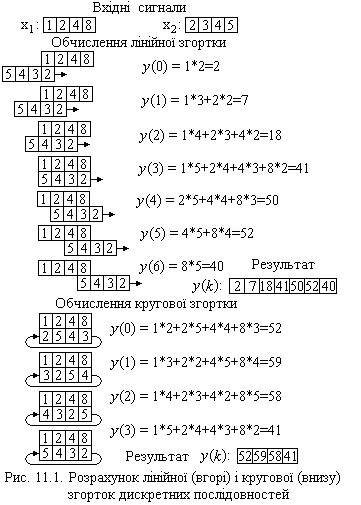
>> y=conv(x1,x2)
y =
2 7 18 41 50 52 40
Реалізуємо розглянутий алгоритм за допомогою функцій fft і ifft:
□ у = fft(x) - обчислює пряме ДПФ для вектора х; якщо х - матриця, перетворення виробляється для кожного її стовпця окремо;
□ у = fft(x, N) — попередньо призводить вихідні дані до розміру N, обрізуючи їх або доповнюючи нулями;
□ х = ifft(y) і х = ifft(y, N) — аналогічні варіанти виклику для функції зворотного ДПФ.
Функції fft і ifft входять в базову бібліотеку MATLAB. Обчислення організовані так, що реалізується максимально можливе для кожної довжини вихідного вектора прискорення обчислень: довжина вектора (число рядків в матриці) x розкладається на прості множники, число цих множників відповідає кількості ступенів ШПФ, а самі множники визначають коефіцієнти проріджування на різних щаблях ШПФ.
function Example11_3
x1=[1 2 4 8];
x2=[2 3 4 5];
y=conv(x1,x2)
X1=fft(x1, 8);
X2=fft(x2, 8);
Y=X1.*X2;
y_fft=ifft(Y)
y =
2 7 18 41 50 52 40
y_fft =
2.0000 7.0000 18.0000 41.0000 50.0000 52.0000 40.0000 0
Недоліком описаного методу фільтрації є те, що вхідний сигнал обробляється відразу цілком, тобто розрахунки можна почати тільки після закінчення вхідного сигналу. Однак на практиці в більшості випадків необхідно обробляти відліки вхідного сигналу в міру їх надходження.
Можливим рішенням проблеми є блокова, або секційна, обробка вхідного сигналу. При цьому послідовність вхідних відліків ділиться на блоки (секції) заданого розміру і ці блоки піддаються фільтрації в частотній області окремо. При виборі розміру блоку необхідно реалізувати компроміс між числом операцій (чим більше розмір блоку, тим ефективніше використання алгоритму ШПФ) і затримкою отримання вихідного сигналу (чим менше розмір блоку, тим менше ця затримка).
При використанні блочної фільтрації необхідно розібратися в ідеї об'єднання вихідних сигналів, отриманих при обробці окремих блоків. Розглянемо її на конкретному прикладі. Нехай вхідний сигнал х і імпульсна характеристика фільтра h мають такий вигляд:
>>h=[1 4 2];
>>x=[1 2 3 4 5 4 3 3 2 2 1 1];
Перш за все вираховується лінійна згортка
>>y=conv(x,h)
y =
1 6 13 20 27 32 29 23 20 16 13 9 6 2
Далі розбиваємо вхідний сигнал на два блоки по 6 відліків і обробляємо їх окремо:
>>x1=x(1:6);
>>x2=x(7:end);
>>y1=conv(x1,h)
y1 =
1 6 13 20 27 32 26 8
>>y2=conv(x2,h)
y2 =
3 15 20 16 13 9 6 2
Аналізуючи отримані результати, ми помітимо, що перші шість відліків вектора yl збігаються з першими шістьма елементами повного вихідного сигналу у. Останні шість відліків вектора у2, у свою чергу, збігаються з шістьма останніми елементами повного вихідного сигналу у. Два «середніх» елемента (7-й і 8-й) вектора у можуть бути отримані підсумовуванням двох останніх елементів вектора yl з двома першими елементами вектора у2.
>>y_add=[y1(1:6) y1(7:8)+y2(1:2) y2(3:end)]
y =
1 6 13 20 27 32 29 23 20 16 13 9 6 2
Результат збігається з отриманим раніше. Отже, в загальному випадку фільтрація організується так.
1. Вхідний сигнал розбивається на блоки довжиною N відліків.
2. Кожен блок фільтрується незалежно. Довжина вихідного сигналу становить N + М - 1 відліків, де М - довжина імпульсної характеристики фільтра. Для підвищення ефективності фільтрація здійснюється в частотній області з використанням ШПФ.
3. Блоки вихідного сигналу об'єднуються, при цьому їх крайні М - 1 відліків перекриваються і сумуються.
Даний алгоритм називається методом перекриття з підсумовуванням (overlap-add). Інший можливий варіант - перекриття з накопиченням (overlap-save). При цьому вхідний сигнал розбивається на блоки, що перекриваються по краях на М - 1 відліків, а у вихідного сигналу для кожного блоку відкидаються крайні «хвости» з М - 1 відліків з кожного боку. Після цього вихідні блоки поєднуються без перекриття.
function Example11_4
h=[1 4 2];
x=[1 2 3 4 5 4 3 3 2 2 1 1];
y=conv(x,h)
x1=x(1:6);
x2=x(7:end);
y1=conv(x1,h)
y2=conv(x2,h)
y_add=[y1(1:6) y1(7:8)+y2(1:2) y2(3:end)]
y =
1 6 13 20 27 32 29 23 20 16 13 9 6 2
y1 =
1 6 13 20 27 32 26 8
y2 =
3 15 20 16 13 9 6 2
y_add =
1 6 13 20 27 32 29 23 20 16 13 9 6 2
Питання для самоперевірки
1. Який зв'язок ДПФ і спектру дискретного аналізу?
2. Яка взаємозв'язок ДПФ і фільтрації?
3. Як виконується дискретна фільтрація за допомогою ДПФ?