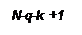ЗАДАЧА ПРО НАЙКОРОТШИЙ ШЛЯХ

Кожен багатокроковий процес прийняття рішень може бути зведений до задачі знаходження найкоротшого шляху (ЗЗНШ) у спрямованій ациклічній слоїстій мережі (САСМ). Саме з такої точки зору і будемо розглядати ЗЗНШ.

Розглянемо ряд визначень.

Спрямована мережа - це трійка , де - непорожня кінцева множина вершин (), 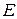- множина дуг: .

Наявність дуги 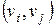вказує на можливість прямого руху з вершинидо вершини . З того, що , не випливає, що . Тому ці дуги називають спрямованими (орієнтованими).

Кожній дузі 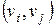поставлено у відповідність деяке дійсне число - довжина дуги, що з'єднує вершини і , , .

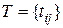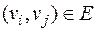Шляхом називається кінцева послідовність вершин, таких, що 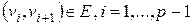. Довжина шляху – сума довжин дуг, що входять у нього.

Шлях, у якого 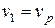, 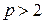називається циклом.

Мережа називається ациклічною, якщо вона не містить жодного циклу.

В спрямованій ациклічній мережі завжди можна позначити вершини цілими числами від 1 до , таким чином, що для кожної дуги буде справедлива нерівність . Далі будемо вважати, що така нумерація проведена.

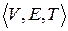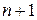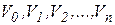
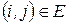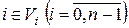Спрямовану ациклічну мережу будемо називати слоїстою, якщо всі її вершини можуть бути розбиті на підмножин (слоїв), що взємно не перетинаються , таким чином, що кожна дуга може зв'язувати лише вершини із сусідніх слоїв. Тобто, якщо й , то .

Відзначимо, що в загальному випадку й 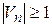, і має сенс розв’язувати задачі при кількості слоїв 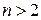(рис. 7).

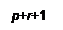
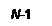
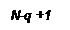
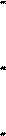
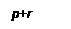
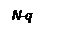
Рис. 7

Кожна спрямована ациклічна мережа може бути зведена до слоїстої мережі шляхом введення фіктивних вершин і дуг. Наступний приклад ілюструє цей процес. Нехай маємо спрямовану ациклічну мережу (рис. 8). Ця мережа не є слоїстою.

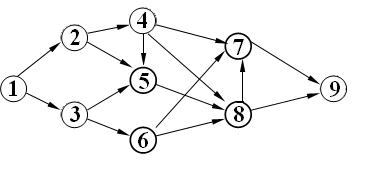
Рис. 8

Після додавання фіктивних вершин 4', 5', 6', 7' і 8', а також дуг з нульовими вагами, що входять у ці вершини, одержали слоїсту мережу (рис 9).

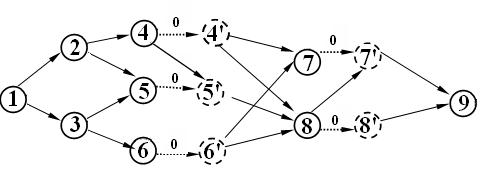
Рис. 9

Розглянемо задачу знаходження найкоротшого шляху в САСМ з погляду ідей і прийомів ДП.

Нехай . Мета задачі – знайти найкоротший шлях між вершинами 1 і .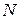

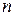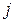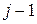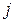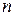Задача може бути інтерпретована як багатокрокова (багатоетапна). У ній кожен шлях складається рівно з дуг - кроків. Під -м кроком (етапом) будемо розуміти перехід зі слою до слою . Таким чином, при переході з вершини 1 у вершину буде зроблено рівно кроків.

На початку кроку 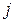система може перебувати в одній з вершин . У цьому випадку кажуть, що система перебуває в одному з можливих станів . Для кожної вершини відомі дуги, що з'єднують її з однією з вершин множини 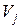. Інакше кажучи, для кожного стану відомі варіанти розв’язків (управлінь), що переводять систему в один із станів наступного кроку. Таким чином, варіантами розв’язків для стану : є всі дуги (s,k), що починаються в вершині .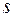

Нехай 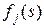- довжина найкоротшого шляху на кроках від 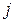до 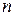включно, за умови, що на початку кроку 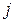система перебуває в стані 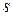. Якщо на кроці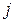, перебуваючи у вершині 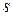, ми приймаємо рішення піти по дузі 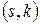, то мінімальна довжина шляху з вершини 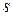в цьому випадку становитиме

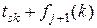
де – довжина найкоротшого шляху від вершини 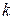до вершини 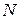, що складається з кроків . Перебравши всі можливі варіанти розв’язків і знайшовши мінімум, отримаємо:

(1)

Цей вираз справедливий і при 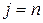, якщо прийняти .

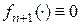З урахуванням позначень, мета нашої задачі – знайти .