Лекция 9. Код Хэмминга и циклические коды

 

Известно несколько разновидностей кода Хэмминга, характеризуемых различной корректирующей способностью. Но в основу построения всех их положен один и тот же метод. Ограничимся рассмотрением лишь принципов построения кодов, исправляющих одиночные ошибки.

Код Хэмминга, как и любой (n, k) код, содержит к информационных и р = п - к избыточных символов. Избыточная часть кода строится таким образом, чтобы при декодировании можно было бы установить не только факт наличия ошибок в принятой комбинации, но и указать номер позиции, в которой произошла ошибка. Это достигается за счет многократной проверки принятой комбинации на четность. Количество проверок равно количеству избыточных символов р. Каждой проверкой должны охватываться часть информационных символов и один из избыточных символов. При каждой проверке получают двоичный контрольный символ. Если результат проверки дает четное число, то контрольному символу присваивается значение 0, если нечетное число - 1. В результате всех проверок получается р - разрядное двоичное число, указывающее номер искаженного символа. Для исправления ошибки достаточно лишь изменить значение данного символа на обратное.

Необходимое количество проверочных символов р (или значность кода n) определяется из соотношения (3.9). Значения проверочных символов и номера их позиций но методике Хэмминга устанавливаются одновременно с выбором контролируемых групп кодовой комбинации. При этом нужно исходить из следующего.

В результате первой проверки получается цифра младшего разряда контрольного числа, указывающего номер искаженного символа. Если результат первой проверки даст 1, то один из символов проверенной группы искажен.

 

Таблица 3.2 Натуральный ряд чисел в двоичной системе чисел

№	Символы разрядов контрольного числа
п.п.

 

Для выяснения вопроса, какой из символов при этом может быть искажен, рассмотрим табл. 3.2 в которой представлен для иллюстрации натуральный ряд четырехзначных контрольных чисел в двоичной системе счисления. Как видно из таблицы, если младший разряд контрольного числа содержит единицу, то искажение должно быть в одной из нечетных позиций кодовой комбинации. Следовательно, первой проверкой должны быть охвачены символы с нечетными номерами: 1, 3, 5, 7, 9 и т. д. (Поряд­ковые номера символов в кодовой комбинации читаются слева направо).

Если результат второй проверки даст 1, то получим 1 во втором разряде контрольного числа. Следовательно, второй проверкой должны быть охвачены символы с номерами, содержащими в двоичной записи единицы во втором разряде: 2, 3, 6, 7, 10.

Аналогично при третьей проверке должны проверяться символы, номера которых в двоичной записи содержат единицы в третьем разряде: 4,5,6,7 и т.д.

Такие рассуждения позволяют образовать табл.3.3 проведения проверок.

 

Таблица 3.3 Схема проведения проверок

№ проверки	Номера проверяемых позиций	Номера позиций контрольных символов
.	1,3,5,7,9… 2,3,6,7,10… 4,5,6,7… 8,9,10… …	.

 

 

Если символы проверяемой кодовой комбинации обозначить через а_i то

проверочные операции S_i можно выразить следующим образом:

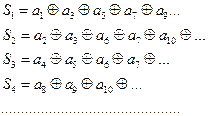(3.18)

С целью упрощения операций кодирования и декодирования целесообразно выбирать такое размещение проверочных символов в кодовой комбинации, при котором каждый из них включается в минимальное число проверяемых групп символов. В связи с этим удобно размещать контрольные символы на позициях, номера которых встречаются только в одной из проверяемых групп: 1, 2, 4, 8, ... (см. табл. 3.3) Следовательно, в кодовой комбинации символы ,,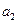,… должны быть проверочными и символы а₃а₅а₆,а₇,а₉...- информационными.

Так как значения информационных символов проставляются заранее, то значения проверочных символов должны быть такими, чтобы сумма единиц, в каждой проверочной группе являлась четным числом.

Представим в качестве примера простую двоичную комбинацию 10011 кодом Хэмминга. При числе информационных символов к=5 в соответствии с (3.9) и табл. 3.1 позиционность кода Хэмминга должна быть n = 9. Так как информационными должны быть третий, пятый, шестой, седьмой, девятый символы, то для рассматриваемого кода

а₃ =1,а₅ =0,а₆ =0,а₇ =1,а₉ =1. Из условия обеспечения четности сумм (3.18) получим следующие значения проверочных символов: а₁ = 1,а₂ =0,а₄ =1,а₈ =1. Следовательно, простому пятиэлементному коду 10011 соответствует девятиэлементный код Хэмминга 101100111.

Пусть теперь при передаче произошла ошибка в пятом символе, т.e. код принял вид 101110111. Тогда в результате первой проверки получим 1, второй - 0, третьей - 1 и четвертой - 0. Таким образом, в результате проверок получено контрольное двоичное число 0101, указывающее на искажение пятого символа.

Рассмотрим основы построения циклических кодов.

Из всех известных корректирующих кодов циклические коды являются наиболее простыми и эффективными. Эти коды могут быть использованы как для обнаружения и исправления независимых ошибок, так и, в особенности для обнаружения и исправления серийных ошибок. Схемы кодирующих и декодирующих устройств для этих кодов просты и представляют собой обычные регистры сдвига. Основное их свойство состоит в том, что каждая кодовая комбинация может быть получена путем циклической перестановки символов комбинации, принадлежащей к этому же коду. Это значит, что если кодовый вектор 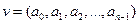принадлежит к циклическому коду V, то вектор получаемый из циклической перестановкой составляющих, т. е. 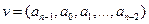, также принадлежит коду V.

Рассмотрение циклических кодов более удобно производить, представляя комбинацию двоичного кода не в виде последовательностей нулей и единиц, а в виде полинома некоторой степени, а именно

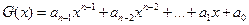(3.19)

где х - условная переменная; а_i - цифры данной системы счисления (в двоичной системе 0 и 1).

Так, например, двоичное семиразрядное число 1010101 может быть записано в виде полинома от переменной х

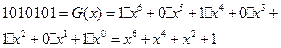(3.20)

Представление кодовых комбинаций в форме (3.19) позволяет свести действия над комбинациями к действиям над многочленами. При этом сложение двоичных многочленов сводится к сложению по модулю 2 коэффициентов при равных степенях переменной х; умножение производится по обычному правилу перемножения степенных функций, однако полученные при этом коэффициенты при данной степени складываются по модулю 2; деление осуществляется по правилам деления степенных функций, при этом операции вычитания заменяются операциями суммирования по модулю 2.

Представление комбинаций в форме (3.19) удобно еще и тем, что упомянутая ранее циклическая перестановка есть результат простого умножения данного полинома на х. Действительно, если одна из кодовых комбинаций выражается полиномом 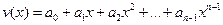, то новая комбинация за счет циклического сдвига будет 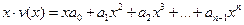. В последнем члене необходимо заменить 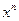на единицу. Следовательно, новая комбинация будет .

Используя представление двоичных кодов в виде полиномов, можно дать следующее определение циклическим кодам.

Циклический код - это такой (n,k) код, который образуется путем умножения простого k - значного кода, выраженного в виде полинома Q(x) степени k -1, на некоторый образующий полином Р(х) степени (n - k).

В результате умножения всех кодовых комбинаций простого k -значного кода на образующий полином Р(х) число разрешенных комбинаций не изменяется и остается равным 2^к , а общее число запрещенных кодовых комбинаций будет равно 2ⁿ -2^к.

Разрешенные комбинации циклического кода образуют некоторое множество комбинаций, отличающееся тем, что отображающие их полиномы делятся без остатка на образующий полином Р (х). При делении полиномов запрещенных комбинаций па образующий полином Р(х) обязательно появится остаток.

Это свойство циклического кода используется для исправления или для обнаружения ошибок. Действительно, если под воздействием помех разрешенная кодовая комбинация трансформируется в запрещенную, то ошибка может быть обнаружена но остатку при делении комбинации на образующий полином Р(х).

Процедура построения циклического кода следующая. Кодовая комбинация простого k-значного кода G(x) умножается на одночлен х^n-k затем делится на образующий полином Р(х), степень которого равна. В результате умножения комбинации G (х) на х^n-k степень каждого одночлена, входящего в G (х), повысится на n - k . При делении произведения х^n-k • G (х) па образующий полипом Р(х) получится частное Q(x) такой же степени, как и G(x),

Результат умножения и деления можно представить в следующем виде:

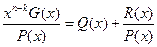(3.21)

где R(x) — остаток от деления x^n-kG(x) на Р(х).

Так как частное Q (х) имеет такую же степень, как и кодовая комбинация G(x) простого кода, то Q(x) является кодовой комбинацией того же простого k-значного кода.

Умножая обе части равенства (3.21) на Р(х) и произведя некоторые

перестановки, получим

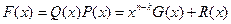(3.22)

В правой части (3.22) знак минус перед R(x) заменен знаком плюс, так как вычитание по модулю 2 сводится к сложению.

Таким образом, кодовая комбинация циклического n - значного кода может быть получена двумя способами:

1) путем умножения кодовой комбинации G(x) простого кода на одночлен x^n-k и добавления к этому произведению остатка R(x), полученного в результате деления произведения x^n-kG(x) на образующий полином Р(х);

2) путем умножения кодовой комбинации Q(x) простого k -значного кода на образующий полином Р(х).

При первом способе кодирования первые к символов полученной кодовой комбинации совпадают с соответствующими символами исходного простого кода.

При втором способе в полученном коде информационные символы не всегда совпадают с символами исходного простого кода.

Такой способ легко реализуем, по вследствие того, что в полученных кодовых комбинациях не содержатся информационные символы в явном виде, усложняется процесс дешифрации.

После исправления ошибок такие комбинации для выделения информационных символов приходится делить на образующий многочлен. Показано, что для любых целых положительных чисел и 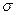существует циклический код значности.

(3.23)

и кодовое расстояние

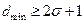(3.24)

При этом число проверочных символов р = n - k не превышает . величины , т. е.

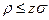(3.25)

Такой код гарантированно исправляет ошибки кратности а и менее, или обнаруживает ошибки кратности 2 а и менее. Кроме того, код обнаруживает все пакеты ошибок, длина которых равна или меньше р.

Соотношения (3.23), (3.24) и (3.25) могут быть использованы для выбора образующего полинома, который нужно производить с учетом того, что степень полинома должна быть равна числу проверочных символов р = n-k. Кроме того, полином Р(х) должен входить в качестве сомножителя в разложение двучлена

(3.26)

Двучлены типа (3.26) обладают тем свойством, что они являются общими кратными для всех без исключения неприводимых (т. е. не делящихся ни на какой другой многочлен) полиномов степени z и разлагаются на множители из всех неприводимых полиномов степени z_i которых делят без остатка число z

Рассмотрим в качестве примера метод построения циклического кода содержащего

к = 4 информационных символа и обеспечивающего устранение однократных ошибок или обнаружение двукратных ошибок

В соответствии с (3.9) и табл.3.1 определяем значность кода n = 7 и количество проверочных символов p = 3.

Для построения циклического кода необходимо выбрать образующий полипом Р(х) степени р =3, который, как указывалось ранее, должен входить в качестве сомножителя в разложение двучлена 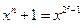. Так как n =7, то этот двучлен имеет вид х⁷ +1. Составляющие его сомножители должны быть неприводимыми полиномами, степени которых являются делителями числа z = 3. К числам, на которые z = 3 делится без остатка, относятся 1 и 3. Следовательно, сомножителями двучлена х⁷+1 должны быть неприводимые полиномы первой и третьей степеней.

Пользуясь таблицами неприводимых полиномов, получим

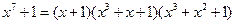(3.27)

Один из сомножителей третьей степени, например , можно взять в качестве образующего полинома.

Для построения циклического кода остается умножить каждую простую четырехсимвольную комбинацию Q(x) на образующий полином. Возьмем в качестве примера простую четырехсимвольную комбинацию Q (х) = 0011. Операция умножения этой комбинации на образующий полином Р(х) дает следующий результат

Таким образом, простая четырехсимвольная комбинация Q (х) = 0011 представляется семисимвольным циклическим кодом F(x) =Q(x)P(x) =0010111.

В заключение рассмотрим один из эффективных способов повышения помехоустойчивости передачи - использование обратного канала, по которому информация может передаваться от приемника к передатчику. Системы, вкоторых применяется передача по обратному каналу, носят общее название систем с обратной связью.

Существует большое число способов построения обратного канала Основные варианты схем обратной связи показаны па puc.3.2.

 

 

Рис 3.2 Системы с обратной связью

 

В варианте 1 обратная связь охватывает только линию связи. В вариантах II и III обратная связь подключена после решающего устройства.

Вариант III отличается тем, что обратная связь охватывает всю систему.

В зависимости от способа использования обратного капала системы с обратной связью могут быть разделены на два основных типа:

• системы с информационной обратной связью (системы со сравнением);

• системы с решающей обратной связью (системы с переспросом).

В системах с информационной обратной связью по обратному каналу передаются все принятые сигналы. На передающей стороне эти сигналы сравниваются с переданными. В случае наличия расхождений осуществляется повторная передача сигнала либо передача данных о необходимых исправлениях.

В системах с решающей обратной связью приемник сам проверяет правильность принимаемого сигнала. При обнаружении искажений приемник посылает по обратному каналу сигнал переспроса па повторение передачи искаженного сигнала.

Таким образом, в системах с информационной обратной связью решение о необходимости повторения передачи принимается на передающей стороне, а в системах с решающей обратной связью - на приемной стороне.

Обратные каналы в системах с информационной обратной связью и в системах с решающей обратной связью используются не в одинаковой степени. Обратный канал в системе с решающей обратной связью загружен обычно значительно меньше, чем в системах с информационной обратной связью, ибо в системах с решающей обратной связью сигнал по обратному каналу поступает лишь в случае обнаружения искажений в переданном сигнале, в то время как в системах с информационной обратной связью каждый принятый сигнал пересылается по обратному каналу на передающую сторону.

Структура сигналов в системах с решающей обратной связью должна быть таковой, чтобы ошибка при передаче могла быть обнаружена на приемной стороне. Это может быть осуществлено лишь при использовании кодов, позволяющих обнаруживать искажения. Исследования показали, что системы с решающей обратной связью, использующие коды с обнаружением ошибок, эффективнее систем без обратной связи, использующих коды с исправлением ошибок. Это объясняется тем, что в системах с решающей обратной связью повторение передачи осуществляется лишь при обнаружении ошибок в переданном сигнале, в то время как в системах с автоматической коррекцией ошибок па приемной стороне независимо от наличия искажений в сигналах постоянно вводится избыточность, требуемая для исправления ошибок.