рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Философия
- /
- Тема 1 Особенности и признаки интеллектуальности информационных систем. Системы с интеллектуальным интерфейсом
Реферат Курсовая Конспект
Тема 1 Особенности и признаки интеллектуальности информационных систем. Системы с интеллектуальным интерфейсом
Тема 1 Особенности и признаки интеллектуальности информационных систем. Системы с интеллектуальным интерфейсом - раздел Философия, Тема 1 Особенности И Признаки Инте...
Тема 1 Особенности и признаки интеллектуальности информационных систем. Системы с интеллектуальным интерфейсом
Принятие решений относительно действий или поведения в той или иной ситуации любых субъектов (людей, роботов, сложных систем упр.) осуществляется на… Любая информационная система (ИС) выполняет следующие функции: воспринимает… Знание имеет двоякую природу: фактуальную и операционную.Программа = алгоритм (правила преобразования данных + управляющая структура) + структура данных.
Т.о. операционные знания (алгоритм) и фактуальные знания (структура данных) неотъемлемы друг от друга. Однако, если в ходе эксплуатации информационных систем выясняется потребность в модификации одного из двух компонентов программы, то возникнет необходимость ее переписывания.
Следствием этого является плохая жизнеспособность ИС, слабая адаптивность к постоянным изменениям информационным потребностям. Невозможность решать задачи в не полностью определенных ситуациях.
В системах, основанных на обработке БД происходит отделение фактуального и операционного знаний друг от друга. Первое организуется в виде БД, второе - в виде программ. Причем, программа может автоматически интегрироваться по запросу пользователя (например, реализация SQL запросов). В качестве посредника между программой и БД выступает программный инструмент доступа данных - СУБД.
СБД=программа ó СУБД óБД
Общие недостатки традиционных ИС: 1. Слабая адаптируемость к изменениям предметной области, 2. Слабая адаптируемость к информационным потребностям пользователей,Системы с интеллектуальным интерфейсом
2. Естественно языковой интерфейс предполагает трансляцию естественно языковых конструкций на внутримашинный уровень представления знаний. Для… Естественно языковой интерфейс используется для: 1. доступа к интеллектуальным БД,Тема 2 Экспертные системы. Архитектура ЭС, база знаний, интеллектуальный интерфейс, механизм вывода, механизм объяснения, механизм приобретения знаний
Экспертные системы.
Достоинства экспертных систем заключаются в возможности принятия решений в уникальных ситуациях, для которых алгоритм заранее неизвестен и… ЭС является инструментом усиливающим интеллектуальные способности эксперта и… 1. Консультанта для неопытных или непрофессиональных пользователей,Тема 3 Классы ЭС
По степени сложности решаемых задач ЭС можно классифицировать следующим образом:
По способу учета временного признака ЭС могут быть статическими и динамическими. Статические системы решают задачи при неизменяемых в процессе решения данных и знаниях, динамические системы допускают такие изменения. Статические системы осуществляют монотонное непрерываемое решение задачи от ввода исходных данных до конечного результата, динамические системы предусматривают возможность пересмотра в процессе решения полученных ранее результатов и данных.
По способу формирования решения ЭС разделяются на 2 класса: аналитические и синтетические. Аналитические системы предполагают выбор решений из множества известных альтернатив (определение характеристик объектов), а синтетические сис. - генерацию неизвестных решений (формирование объектов).
По видам используемых данных и знаний ЭС классифицируются на системы с детерминированными (четко определенными) знаниями и неопределенными знаниями. Под неопределенностью знаний (данных) понимается их неполнота (отсутствие), недостоверность (неточность измерения), двусмысленность (многозначность понятий), нечеткость (качественная оценка вместо количественной).
По числу используемых источников знаний ЭС могут быть построены с использованием одного или множества источников знаний.
Источники знаний могут быть альтернативными (множество миров) или дополняющими друг друга.
В соответствии с перечисленными признаками классификации, как правило, выделяются следующие 4 основные класса ЭС.
Классифицирующие ЭС
К аналитическим задачам прежде всего относятся задачи распознания различных ситуаций, когда по набору заданных признаков (факторов) выявляется сущность некоторой ситуации, в зависимости от которой выбирается определенная последовательность действий. Т.о., в соответствии с исходными условиями среди альтернативных решений находится одно, наилучшим образом удовлетворяющее поставленной цели и ограничениям.
ЭС, решающие задачи распознавания ситуаций, называются классифицирующими, поскольку определяют принадлежность анализируемой ситуации к некоторому классу. В качестве основного метода формирования решений используется метод логического дедуктивного вывода от общего к частному, когда путем подстановки исходных данных в некоторую совокупность взаимосвязанных общих утверждений получается частное заключение.
| Анализ | Синтез | ||
| Детерминирован-ность знаний | Классифици-рующие | Трансформирующие | Один источник знаний |
| Неопределенность знаний | Доопределяю-щие | Многоагентные | Множество источников знаний |
| Статика | Динамика |
Рисунок. Классы ЭС
Доопределяющие ЭС. Решают более сложные аналитические задачи на основе неопределенных исходных данных и знаний (доопределяет недостающие знания). В этом случае экспертная система должна как бы доопределять недостающие знания, а в пространстве решений с различной вероятностью или уверенностью в необходимости их выполнения. В качестве методов работы с неопределенностями могут использоваться байесовский вероятностный подход, коэффициенты уверенности, нечеткая логика.
Доопределяющие ЭС могут использоваться для формирования решения несколько источников знаний. В этом случае могут использоваться эвристические приемы выбора единиц знаний из их конфликтного набора, например, на основе использования приоритетов важности, или получаемой степени определенности результата или значений функций предпочтений.
Для аналитических задач классифицирующего и доопределяющего типов характерны следующие проблемные области:
1. Интерпретация данных - выбор решения из фиксированного множества альтернатив на базе введенной информации о текущей ситуации. Основное назначение - определение сущности рассматриваемой ситуации, выбор гипотез, исходя из фактов. Пример, ЭС анализа финансового состояния предприятия.
2. Диагностика - выявление причин, приведших к возникновению ситуации. Требуется предварительная интерпретация ситуации с последующей проверкой дополнительных фактов, например, выявление факторов снижения эффективности производства.
3. Коррекция - диагностика, дополненная возможностью оценки и рекомендации действий по исправлению отклонений от нормального состояния рассматриваемых ситуаций.
Трансформирующие ЭС.
Относятся к синтезирующим динамическим системам, предполагают повторяющееся преобразование знаний в процессе решения задач, что связано с характером результата, который нельзя заранее предопределить, а также с динамичностью самой предметной области.
В качестве методов решения задач используются:
1. Генерация и тестирование. Когда по исходным данным осуществляется генерация гипотез, а затем проверка сформулированных гипотез на подтверждение поступающими фактами.
2. Предположение и умолчание. Когда по неполным данным подбираются знания об аналогичных классах объектов, которые в дальнейшем динамически адаптируются к конкретной ситуации в зависимости от ее развития.
3. Использование общих закономерностей (метауправления) в случае неизвестных ситуаций, позволяющих генерировать недостающее знание.
Многоагентные системы
Особенности: 1. Проведение альтернативных рассуждений на основе использования различных… 2. Распределенное решение проблем, которые разбиваются на параллельно решаемые подпроблемы, соответствующие…Тема 4 Самообучающиеся системы: индуктивные системы, нейронные сети, системы, основанные на прецедентах, информационные хранилища
В основе самообучающихся систем лежат методы автоматической классификации примеров ситуаций реальной практики (обучение на примерах). Примеры… Обучающая выборка может быть: · «с учителем», когда для каждого примера задается в явном виде значение признака его принадлежности некоторому…Пример построения дерева решений на основе фрагмента таблицы примеров
| Классообр. признак | Признаки классификации | |||
| Цена | Спрос | Конкуренция | Издержки | Качество |
| Низкая | Низкий | Маленькая | Маленькие | Низкое |
| высокая | Низкий | Маленькая | Большие | Высокое |
| Высокая | Высокий | Маленькая | Большие | Низкое |
| Высокая | Высокий | Маленькая | Маленькие | Высокое |
| Высокая | Высокий | Маленькая | Маленькие | Низкое |
| Высокая | Высокий | Маленькая | Большие | Высокое |
Анализ новой ситуации сводится к выбору ветви дерева, которая полностью определяет эту ситуацию. Поиск решения осуществляется в результате последовательной проверки признаков классификации. Каждая ветвь дерева соответствует одному правилу решения:
ЕСЛИ Спрос = «низкий» и ИЗДЕРЖКИ = «маленькие»
ТО ЦЕНА = «низкая»
Примерами инструментальных средств, поддерживающих индуктивный вывод знаний, являются lst Class (Programs in Motion), Rulemaster (Radian Corp.), KAD (ИПС Переяславль-Залесский), ИЛИС (ArgusSoft).
Нейронные сети.
X1
W1
X2 W2
Выход=f (∑wixi)
W3
X3
В результате обучения на примерах строятся математические решающие функции, которые определяют зависимости между входными (xi) и выходными (yi) признаками (сигналами).
Каждая такая функция, называемая по аналогии с элементарной единицей человеческого мозга-нейроном, отображает зависимость значения выходного признака (y) от взвешенной суммы (u) значений входных признаков (xi), в которой вес входного признака (wi) показывает степень влияния входного признака на выходной:
Y=f (∑ Wi*Xi)
i
Решающие функции используются в задачах классификации на основе сопоставления их значений при различных комбинациях значений входных признаков с некоторым пороговым значением. В случае превышения заданного порога считается, что нейрон сработал и таким образом распознал некоторый класс ситуаций. Нейроны используются и в задачах прогнозирования, когда по значениям входных признаков после их подстановки в выражение решающей функции получается прогнозное значение выходного признака.
Функциональная зависимость может быть линейной, но, как правило, используется сигмоидальная форма, которая позволяет вычленять более сложные пространства значений выходных признаков. Такая функция называется логистической.
 |
f(u)=1/(1+exp(-u)) 1
Нейрон “вкл”
Нейрон “выкл.”
0 u
Логистическая функция
Нейроны могут быть связаны между собой, когда выход одного нейрона является входом другого. Т.о., строится нейронная сеть, в которой нейроны, находящиеся на одном уровне, образуют слои.
Выходной
слой Взвешенные
связи
Скрытый
слой












 Узлы
Узлы
Входной слой
Обучение нейронной сети сводится к определению связей (синапсов) между нейронами и установлению силы этих связей (весовых коэффициентов). Алгоритмы обучения нейронной сети упрощенно сводятся к определению зависимости весового коэффициента связи двух нейронов от числа примеров, подтверждающих эту зависимость.
Достоинство нейронных сетей перед индуктивным выводом заключается в решении не только классифицирующих, но и прогнозных задач. Возможность нелинейного характера функциональной зависимости выходных и входных признаков позволяет строить более точные классификации.
Сам процесс решения задач в силу проведения матричных преобразований проводится очень быстро. Фактически имитируется параллельный процесс прохода по нейронной сети в отличие от последовательного в индуктивных системах. Нейронные сети могут быть реализованы и аппаратно в виде нейрокомпьютеров с ассоциативной памятью.
Инструментальные средства:
NeuroSolution, NeuralWorks Professional 2/Plus, Process Advisor? NeuroShell 2, BrainMaiker Pro, NeurOn-line и др.
Системы основанные на прецедентах.
В этих системах БЗ содержит описания не обобщенных ситуаций, а особенно сами ситуации или прецеденты. Тогда поиск решения проблемы сводится к поиску по аналогии (выводу от частного к частному):
1. получение подробной информации о текущей проблеме,
2. сопоставление полученной информации со значениями признаков прецедентов из БЗ,
3. выбор прецедента из БЗ, наиболее близкого к рассматриваемой проблеме,
4. в случае необходимости выполняется адаптация выбранного прецедента к текущей проблеме
5. проверка корректности каждого полученного решения,
6. занесение детальной информации о полученном решении в БЗ.
Также как и для индуктивных систем, прецеденты описываются множеством признаков, по которым строятся индексы быстрого поиска. Но в отличие от индуктивных систем допускается поиск с получением множества допустимых альтернатив, каждая из которых оценивается некоторым коэффициентом уверенности.
Далее наиболее подходящие решения адаптируются по специальным алгоритмам к реальным ситуациям. В качестве методов адаптации в основном применяют методы повторной конкретизации переменных, уточнения параметров, замены одних компонентов решения другими. Обучение системы сводится к запоминанию каждой новой обработанной ситуации с принятыми решениями в базе прецедентов.
Пример инструментальных средств поддержки БЗ прецедентов:
CBR-Express, REMIND, ReCall, KATE tools и др.
Извлечение знаний на основе информационных хранилищ
Типичными задачами оперативного ситуационного анализа, решаемых на основе информационных хранилищ, являются: · Определение профиля потребителей конкретного товара; · Предсказание изменений ситуации на рынке;Тема 5 Прикладное значение ИИС
<<Нужно прикрепить презентации>>
Тема 6 Этапы создания ЭС. Инструментарии построения ЭС. Классификация
Процесс создания экспертной системы, как сложного программного продукта, выполняется методом прототипного проектирования, сущность которого сводится к постоянному наращиванию базы знаний, начиная с логической стадии.

Прототипная технология создания экспертной системы означает, что простейший прототип будущей системы реализуется с помощью любого подручного инструментального средства еще на этапе идентификации и концептуализации, в дальнейшем этот прототип детализируется, концептуальная модель уточняется, реализация выполняется в среде окончательно выбранного инструментального средства. После каждого этапа возможны возвраты на уже выполненные этапы проектирования, что способствует постепенному проникновению инженера по знаниям в глубину решаемых проблем, эффективности использования выделенных ресурсов, сокращению времени, постоянному улучшению компетентности и производительности системы.
Этапы создания ЭС представлены на рисунке:

Этап 1. Идентификация
- обучение и консультация неопытных пользователей; - распространение и использование уникального опыта экспертов; - автоматизация работы экспертов по принятию решений;Этап 2. Концептуализация
- объектная модель описывает структуру предметной области как совокупности взаимосвязанных объектов; - функциональная модель отражает действия и преобразования над объектами; - поведенческая модель рассматривает взаимодействия объектов во временном аспекте.Этап 3. Формализация
На этапе формализации все ключевые понятия и отношения, выявленные на этапе концептуализации, выражаются на некотором формальном языке, предложенном… На этапе формализации реализуются следующие модели: Логическая модель реализует и объекты, и правила с помощью предикатов первого порядка, является строго формализованной…Этап 4. Реализация
Особенности реализации экспертной системы во многом определяются характером инструментального средства, в качестве которого могут выступать… Создается прототип экспертной системы, включающий базу знаний и другие… Так, оболочки имеют реализованные механизмы вывода, накопления, объяснения знаний, диалоговый компонент, что, с одной…Этап 5. Тестирование
С точностью работы связаны такие характеристики, как правильность делаемых заключений, адекватность базы знаний проблемной области, соответствие… Прототип проверяется на удобство и адекватность интерфейсов ввода-вывода,…Этап 6. Опытная эксплуатация
Проверяется пригодность экспертной системы для конечных пользователей. По результатам этого этапа может потребоваться существенная модификация экспертной системы. На этом этапе осуществляется сбор критических замечаний и внесение необходимых изменений. В результате опытной эксплуатации может потребоваться разработка новых специализированных версий, учитывающих особенности проблемных областей.
Лабораторная работа 1 «Выбор инструментальных средств реализации ЭС. Прикладной пакет Resolver»
Лабораторная работа 2 «Построение экспертных систем с использованием четкой логики (по правилам if / then и с помощью дерева правил)»
Тема 7 Основы теории нечеткой логики. Нечеткие множества. Лингвистические переменные. Логические операции с нечеткими множествами
Основой систем нечеткой логики является математическая теория нечетких множеств, которая берет начало со статьи американского ученого Лотфи Заде, опубликованной под названием "Fuzzy Sets" в 1965 году. В настоящее время эта теория получила достаточно глубокое развитие, а системы на базе нечеткой логики нашли широкое применение в промышленности от производства фотоаппарата, стиральных машин, микроволновых печей до управления крупными промышленными производствами и систем поддержки принятия решения.
В большинстве решаемых человеком задач не требуется высокая точность. Наоборот, часто приходится находить разумный компромисс между понятиями "точность" и "важность" при общении с реальным миром.
Определение лингвистической переменной (формальное)
Лингвистической переменной называется пятерка (х, Т(х), Х, G, М), где х-имя переменной; Т(х)-множество имен лингвистических значений переменной х, каждое из которых является нечетким множеством на множестве Х, G есть синтаксическое правило для образования имен значений х и М есть семантическое правило для ассоциирования каждой величины значения с ее понятием.
Определение лингвистической переменной (интуитивное)
Если переменная может принимать значения слов в естественном языке (например, "маленький", "быстрый" и т.п.), то эта переменная определяется как лингвистическая переменная. Слова, значения которых принимает лингвистическая переменная, обычно обозначают собой нечеткие множества. Лингвистическая переменная может принимать своими значениями либо слова, либо числа.
Нечеткое множество – это такое множество, которое образуется путем введения обобщенного понятия принадлежности, т.е. расширения двухэлементного множества значений функции принадлежности {0,1} до отрезка [0,1]. Это означает, что переход от полной принадлежности объекта множеству к его полной непринадлежности происходит не скачком, как в обычных "четких" множествах, а плавно, постепенно, причем степень принадлежности элемента множеству выражается числом из интервала [0,1].
Т.о., нечеткое множество 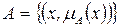 определяется математически как совокупность упорядоченных, пар, составленных из элементов x множества X и соответствующих им степеней принадлежности
определяется математически как совокупность упорядоченных, пар, составленных из элементов x множества X и соответствующих им степеней принадлежности 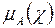 или непосредственно в виде функции
или непосредственно в виде функции 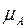 :X → [0,1] .
:X → [0,1] .
Пример. Множество высоких людей
Пусть х есть лингвистическая переменная, обозначающая "рост человека", а ее функция принадлежности к множеству высоких людей  A:X
A:X {0,1}, где Х - множество, включающее в себя все возможные значения роста человека, задана следующим образом:
{0,1}, где Х - множество, включающее в себя все возможные значения роста человека, задана следующим образом:
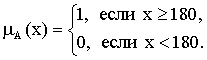
Тогда множество "высоких людей" задается выражением A={x|  A(x)=1}, х
A(x)=1}, х 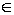 X. Графически это представлено на рисунке (сплошная линия).
X. Графически это представлено на рисунке (сплошная линия).

Однако в реальной жизни такое понятие, как "рост высокого человека", является субъективным, т.е. зависит от индивидуума, делающего оценку. Одни считают, что высокий человек должен быть ростом более 170 см, другие - более 180 см, третьи - более 190 см. Нечеткие множества позволяют учесть такую размытость оценок. Так, пусть функция принадлежности  A:X
A:X {0,1} имеет вид, представленный на рисунке 1 пунктирной линией. Тогда множество А ("высоких людей") задается множеством пар А={x,
{0,1} имеет вид, представленный на рисунке 1 пунктирной линией. Тогда множество А ("высоких людей") задается множеством пар А={x,  A(x)}, х
A(x)}, х 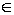 X и является нечетким множеством.
X и является нечетким множеством.
Таким образом, человек ростом 145 см будет принадлежать множеству А со степенью принадлежности  A(145)=0, человек ростом 165 см -
A(145)=0, человек ростом 165 см -  A(165) = 0,3, ростом 185 см -
A(165) = 0,3, ростом 185 см -  A (185)= 0,9, a ростом 205 см -
A (185)= 0,9, a ростом 205 см -  A(205)=1.
A(205)=1.
Можно сказать, что в нечеткой логике правдивость каждого утверждения рассматривается в рамках степени правдивости, которая может также рассматриваться как степень уверенности эксперта, делающего оценку, в том, что элемент х принадлежит множеству А.
Из вышесказанного можно сделать следующие выводы:
1) нечеткие множества описывают неопределенные понятия (быстрый бегун, горячая вода, жаркая погода);
2) нечеткие множества допускают возможность частичной принадлежности к ним (пятница - частично выходной день (укороченный), погода скорее жаркая);
3) степень принадлежности объекта к нечеткому множеству определяется соответствующим значением функции принадлежности на интервале [0,1] (пятница принадлежит к выходным дням со степенью принадлежности 0,3);
4) функция принадлежности ставит в соответствие объекту (или логической переменной) значение степени его принадлежности к нечеткому множеству.
 Нечеткое множество А называется нормальным, если верхняя граница его функции принадлежности равна единице, т.е.
Нечеткое множество А называется нормальным, если верхняя граница его функции принадлежности равна единице, т.е.
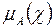 =1,
=1,
если
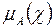 <1,то нечеткое множество называется субнормальным.
<1,то нечеткое множество называется субнормальным.
 Нечеткое множество пусто, если
Нечеткое множество пусто, если 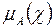 =0 для любых х.
=0 для любых х.
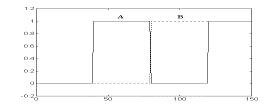
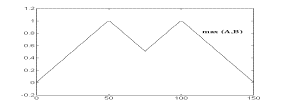
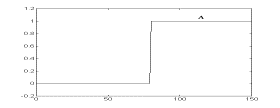
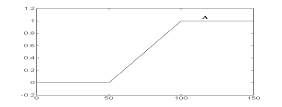
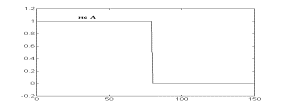
Логические операции с нечеткими множествами. Одной из важных вещей для понимания механизма нечеткой логики является то, что она может рассматриваться как расширение стандартной, хорошо известной булевой логики (подобно тому, как нечеткие множества являются расширением обычных множеств). Другими словами, если рассматривать нечеткие значения в их экстремумах, т.е. в 1 (абсолютная правда) и в 0 (абсолютная ложь), то можно применять стандартные логические операции: И, ИЛИ, НЕ. В нечеткой логике истинность каждого утверждения рассматривается в определенной степени. В нечеткой логике по аналогии с операциями И и ИЛИ вводятся операции min(A,В) и max(А,В), а операции НЕ соответствует операция 1-А. Графически это представлено на рисунках.




| а | б |
Рисунок - Операция min(А,В): а - "четкая" логика; б - "нечеткая" логика


| а | б |
Рисунок - Операция max(А,В): а - "четкая" логика; б- "нечеткая" логика

| а | б |
Рисунок - Операция 1-А: а - "четкая" логика; б- "нечеткая" логика
Пересечением А 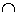 В двух нечетких множеств А и В на множестве Х является нечеткое множество на множестве Х с функцией принадлежности, определяемой для любого х
В двух нечетких множеств А и В на множестве Х является нечеткое множество на множестве Х с функцией принадлежности, определяемой для любого х 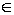 Х как
Х как  .
.
Объединением А  В двух нечетких множеств А и В на множестве Х является нечеткое множество на множестве Х с функцией принадлежности, определяемой для любого х
В двух нечетких множеств А и В на множестве Х является нечеткое множество на множестве Х с функцией принадлежности, определяемой для любого х 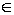 Х как
Х как 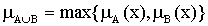 .
.
Дополнением 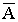 нечеткого множества А на множестве Х является нечеткое множество на множестве Х с функцией принадлежности, определяемой для любого х
нечеткого множества А на множестве Х является нечеткое множество на множестве Х с функцией принадлежности, определяемой для любого х 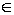 Х как
Х как 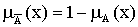 .
.
Лабораторная работа 3«Построение экспертных систем с использованием нечеткой логики. Формирование базы знаний и построение функций принадлежности»
Самостоятельная работа «Работа с конспектом лекций»
Тема 8 Классификация систем нечеткой логики
Системами нечеткой логики называются системы, которые оперируют с нечеткими понятиями, такими как нечеткие множества, лингвистические переменные и т.п., и используют при этом нечеткую логику. Системы нечеткой логики могут быть классифицированы по трем основным типам:
1) простые системы нечеткой логики (pure Fuzzy Logic Systems);
2) нечеткие системы Такаги и Суджено (Takagi and Sugeno);
3) системы нечеткой логики с фаззификатором и дефаззификатором.
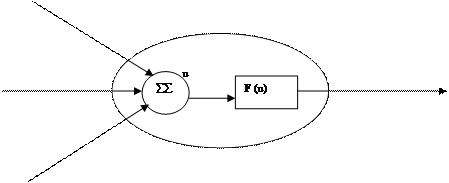
Простые системы нечеткой логики. Базовая конфигурация простой системы нечеткой логики представлена на рисунке.
Базис нечетких правил содержит набор нечетких IF-THEN (ЕСЛИ-TO) правил, а механизм нечеткого вывода на основе принципов нечеткой логики использует эти IF-THEN-правила для отображения нечетких множеств из входящего множества высказываний Х в нечеткие множества из множества высказываний Y на выходе системы.

Рисунок - Простая система нечеткой логики
Практика показывает, что эти нечеткие IF-THEN-правила обеспечивают удобный механизм для представления знаний человека-эксперта.
Если присутствует обратная связь, как показано на рисунке, то мы имеем так называемую нечеткую динамическую систему, т.е. простую систему нечеткой логики, у которой входы зависят от ее выходов. Структура простой системы нечеткой логики является существенной частью систем нечеткой логики. В общем случае, когда лингвистическая информация от эксперта переводится в количественные показатели, принципы нечеткой логики используются для систематизации информации.
Главным недостатком простых систем нечеткой логики является то обстоятельство, что ее входы и выходы - нечеткие множества, тогда как в большинстве технических систем входы и выходы являются переменными, принимающими реальные значения.
Нечеткие системы Такаги и Суджено. Такаги и Суджено предложили использовать IF-THEN-правила:
L(p): IF x1 есть F1p и . . . и xn есть Fnp THEN yp = C0p + C1p x1 +. . .+ Cnp xn,
где Fip - нечеткие множества;
Сi - параметры, принимающие реальные значения;
yp - выход системы, соответствующий правилу L(p); p=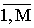 .
.
Таким образом, они рассматривали правила, у которых часть IF является нечеткой, но "четкой" является часть THEN, и выход является линейной комбинацией переменных на входе. Выход нечеткой системы Такаги-Суджено есть взвешенное среднее:

где вес wp вычисляется как:
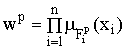
Конфигурация нечеткой системы Такаги-Суджено представлена на рисунке.

Рисунок - Система нечеткой логики Такаги-Суджено
Преимуществом систем нечеткой логики такого типа является то, что они описываются компактной системой уравнений. Для них могут быть легко разработаны методы оценки параметров и выбора порядка системы М.
Слабое место таких систем нечеткой логики заключается в том, что часть THEN в IF-THEN-правиле не является нечеткой, что не позволяет естественным образом получать нечеткие правила от человека-эксперта.
Тема 9 Системы нечеткой логики с фаззификатором и дефаззификатором. Методика построения систем нечеткой логики в RESOLVER’е и в среде MatLab
Базовая конфигурация системы нечеткой логики с фаззификатором и дефаззификатором представлена на рисунке. Рисунок - Система нечеткой логики с фаззификатором и дефаззификаторомПример системы нечеткой логики.
Рассмотрим использование систем нечеткой логики для реализации функций принятия решения на межцеховом уровне машиностроительного предприятия на примере функции "принятие оптимального плана".
Задача принятия оптимального плана заключается в выборе номенклатуры выпускаемых изделий таким образом, чтобы целевая функция 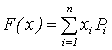 , где xi - i-е изделие; Pi - планируемая прибыль от реализации i-го изделия, принимала максимальное значение. На эту формулу накладываются ограничения, связанные с производственными мощностями предприятия. Данная формула описывает идеальную ситуацию, когда все заказчики той или иной продукции обладают стопроцентной платежеспособностью. Реальная жизнь вносит свои коррективы, и формула для вычисления целевой функции приобретает следующий вид:
, где xi - i-е изделие; Pi - планируемая прибыль от реализации i-го изделия, принимала максимальное значение. На эту формулу накладываются ограничения, связанные с производственными мощностями предприятия. Данная формула описывает идеальную ситуацию, когда все заказчики той или иной продукции обладают стопроцентной платежеспособностью. Реальная жизнь вносит свои коррективы, и формула для вычисления целевой функции приобретает следующий вид:  где ki - коэффициент платежеспособности заказчика. Понятно, что платежеспособность является вполне нечетким понятием и определение коэффициента платежеспособности предприятия является сложной задачей принятия решения. В современных условиях российской экономики платежеспособность предприятия определяется не только наличием денежных средств на банковском счету или возможностью их своевременного привлечения из других источников, но и наличием изделий или материалов, способных заинтересовать предприятие-поставщика в качестве так называемого "бартера".
где ki - коэффициент платежеспособности заказчика. Понятно, что платежеспособность является вполне нечетким понятием и определение коэффициента платежеспособности предприятия является сложной задачей принятия решения. В современных условиях российской экономики платежеспособность предприятия определяется не только наличием денежных средств на банковском счету или возможностью их своевременного привлечения из других источников, но и наличием изделий или материалов, способных заинтересовать предприятие-поставщика в качестве так называемого "бартера".
В связи с этим функция принятия решения по заданию коэффициента платежеспособности была реализована представленной на рисунке системой нечеткой логики с двумя входами, одним выходом и тремя правилами. Входами системы являются экспертные балльные оценки наличия денег на счету заказчика и наличия интересующего предприятие бартера. Минимальное количество баллов (0) соответствует абсолютной уверенности дающего оценку эксперта в том, что заказчик не имеет на счету денежных средств и не сможет их вовремя привлечь для оплаты поставляемых ему изделий, а имеющийся в его распоряжении бартер абсолютно не нужен предприятию. Максимальное количество баллов (10) соответствует обратному положению вещей. Оценки о наличии денежных средств и полезности бартера выносятся разными специалистами. Оценка наличия денежных средств на счету заказчика производится специалистами отдела собственной безопасности предприятия и осуществляется по косвенным признакам. Полезность бартера оценивают специалисты из отдела снабжения.
Выходом системы нечеткой логики является значение коэффициента платежеспособности, который принимает значения от 0 до 1.
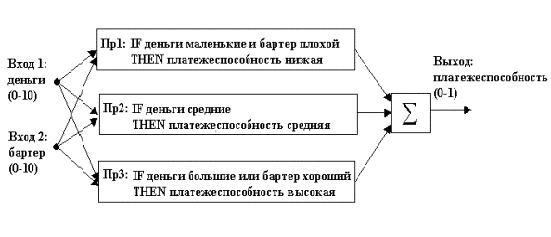
Система работает следующим образом. Информационный поток движется слева направо, от двух входов к одному выходу. Параллельная природа выполнения правил является одним из важных аспектов систем нечеткой логики. Вместо резкого переключения между моделями (правилами) в точках перехода получается гладкий переход от области, в которой поведение системы описывается одним правилом, к области, где оно описывается другим правилом.
Для входов системы определены соответствующие им нечеткие множества и заданы определяющие эти множества функции принадлежности. В данном случае входы задаются на множестве чисел (баллов) от 0 до 10. Экспертом, принимавшим участие в построении системы нечеткой логики, были заданы три правила, использующие нечеткие множества, и определены функции их принадлежности. Для наличия денег на счету заказчика (переменная "деньги") - это нечеткие множества "маленькие", "средние" и "большие", для переменной "бартер" - "плохой" и "хороший", для переменной "платежеспособность" -"низкая", "средняя" и "высокая".
Прежде чем применить тот или иной метод импликации, необходимо учитывать вес правила. Каждое правило может иметь свой вес (число от 0 до 1) в зависимости от того, насколько это правило является важным. Вес правила накладывается на выход IF-части. В данном случае все правила приняты равноценными, и вес каждого правила равен 1.
Метод импликации определяется как формирование вывода из правила на основе заданных условий. Входом процесса импликации является число, полученное из условий (степень истинности условия), а выходом - нечеткое множество. Для данной системы нечеткой логики был выбран самый простой и хорошо себя зарекомендовавший метод импликации по минимуму.
В случае, когда несколько правил работают параллельно, необходимо объединить (агрегатировать) нечеткие множества, представляющие выходы отдельных правил, в одно нечеткое множество для подготовки к заключительному шагу - дефаззификации. Входом процесса агрегатирования является набор нечетких множеств, полученных из каждого правила путем импликации. Его выходом является одно нечеткое множество для каждой выходной переменной. В данном случае для агрегатирования нечетких множеств используется операция объединения.
На рисунке показана общая схема предлагаемой системы нечеткой логики.

Заметим, что так как методы агрегатирования являются коммутативными (что должно выполняться всегда), то порядок, в каком стоят правила, не имеет значения. Для иллюстрации работы системы на рисунке 9 заданы входы "деньги=3" и "бартер=8". Выходом операции агрегатирования для заданных входов является нечеткое множество с функцией принадлежности, представленной на рисунке.
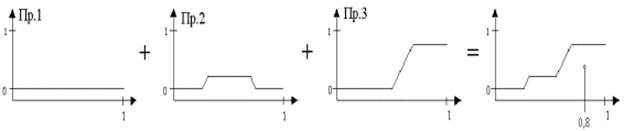
Дефаззификация выходного нечеткого множества методом центра тяжести дает для приведенного примера выходное значение коэффициента платежеспособности 0,8. Заметим, что все нечеткие множества заданы на соответствующих множествах. Для денег и бартера - на множестве баллов от 1 до 10, для коэффициента платежеспособности - на непрерывном множестве от 0 до 1.
Лабораторная работа 4 «Построение нечетких систем с помощью ППП Fuzzy Logic Toolbox среды MatLab. Проектирование систем типа Мамдани»
Лабораторная работа 5 «Построение нечетких систем с помощью ППП Fuzzy Logic Toolbox среды MatLab. Проектирование систем типа Сугэно»
Лабораторная работа 6«Оформление ЭС, командного файла. Тестирование ЭС. Демонстрация ЭС»
Лабораторная работа 7 «Итоговое занятие»
– Конец работы –
Используемые теги: Тема, особенности, знаки, интеллектуальности, информационных, систем, системы, интеллектуальным, интерфейсом0.125
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Тема 1 Особенности и признаки интеллектуальности информационных систем. Системы с интеллектуальным интерфейсом
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов