История возникновения теории нечетких множеств
Теория нечетких множеств (fuzzy sets theory) ведет свое начало с 1965г., когда профессор Лотфи Заде (Lotfi Zadeh) из университета Беркли опубликовал основополагающую работу “Fuzzy Sets” в журнале “Information and Control”. Концепция нечеткого множества зародилась у Заде “как неудовлетворенность математическими методами классической теории систем, которая вынуждала добиваться искусственной точности, неуместной во многих системах реального мира, особенно в так называемых гуманистических системах, включающих людей”.
Началом практического применения теории нечетких множеств можно считать 1975г., когда Мамдани и Ассилиан построили первый нечеткий контролер для управления простым паровым двигателем. В 1982 Холмблад и Остергад разработали первый промышленный нечеткий контроллер, который был внедрен в управление процессом обжига цемента на заводе в Дании. Успех первого промышленного контролера, основанного на нечетких лингвистических правилах “Если - то” привел к всплеску интереса к теории нечетких множеств среди математиков и инженеров. Несколько позже Бартоломеем Коско была доказана теорема о нечеткой аппроксимации, согласно которой любая математическая система может быть аппроксимирована системой, основанной на нечеткой логике. Другими словами, с помощью естественно-языковых высказываний-правил “Если - то”, с последующей их формализацией средствами теории нечетких множеств, можно сколько угодно точно отразить произвольную взаимосвязь “входы-выход” без использования сложного аппарата дифференциального и интегрального исчислений, традиционно применяемого в управлении и идентификации.
Системы, основанные на нечетких множествах, разработаны и успешно внедрены в таких областях, как: управление технологическими процессами, управление транспортом, медицинская диагностика, техническая диагностика, финансовый менеджмент, биржевое прогнозирование, распознавание образов. Спектр приложений очень широкий - от видеокамер и бытовых стиральных машин до средств наведения ракет ПВО и управления боевыми вертолетами. Практический опыт разработки систем нечеткого логического вывода свидетельствует, что сроки и стоимость их проектирования значительно меньше, чем при использовании традиционного математического аппарата, при этом обеспечивается требуемый уровень робастности и прозрачности моделей.
3.1.1. Четкие и нечеткие множества
3.1.1.1. Четкие множества
Определение. Множество А – четкое множество, если А – часть некоторого универсального для данной прикладной задачи множества U, характеризующегося условиями:
· Все элементы множества четко различимы между собой, во множестве нет повторяющихся элементов, нескольких экземпляров некоторых элементов;
· Относительно каждого элемента uÎU можно четко определить, принадлежит он данному множеству или нет.
Эти условия позволяют охарактеризовать четкое множество его характеристической функцией, заданной на универсальном множестве U и принимающей значения в множестве {0, 1}:
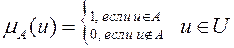 .
.
Отказ от первого условия приводит к более общему, чем множество, понятию комплекта, допускающего наличие нескольких экземпляров некоторых элементов. Комплект 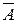 характеризуется функцией экземплярности, заданной на универсальном множестве U и принимающей значения во множестве неотрицательных целых чисел:
характеризуется функцией экземплярности, заданной на универсальном множестве U и принимающей значения во множестве неотрицательных целых чисел:  Î{0, 1, 2, …} – число экземпляров элемента uÎU в комплекте
Î{0, 1, 2, …} – число экземпляров элемента uÎU в комплекте 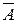 .
.
Отказ от второго условия приводит к более общему, чем множество, понятию нечеткого множества, допускающего определение лишь некоторой степени принадлежности элементов такому множеству.
3.1.1.2. Нечеткое множество
Нечеткое множество А характеризуется функцией принадлежности, заданной на универсальном множестве U и принимающей значения во множестве чисел 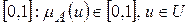 , при этом
, при этом 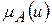 указывает на степень принадлежности элемента
указывает на степень принадлежности элемента 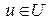 нечеткому множеству.
нечеткому множеству.
Легко заметить, что четкое множество – частный случай нечеткого множества, в этом случае функция принадлежности может принимать только два возможных значения 0 или 1 и является ни чем иным, как характеристической функцией четкого множества.
Определение. Нечетким подмножеством А множества Х называется совокупность пар вида 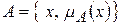 , где
, где 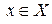 , а
, а 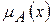 – функция принадлежности, ставящая в соответствие множеству Х отрезок
– функция принадлежности, ставящая в соответствие множеству Х отрезок 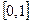 .
.
Х – базовое множество или базовая шкала. Значение функции принадлежности для каждого элемента х называется его степенью принадлежности элемента Х нечеткому множеству А. В множество  не включаются элементы, для которых
не включаются элементы, для которых 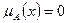 .
.
Нечеткое множество Æ – пустое, если  для каждого
для каждого 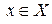 .
.
Нечеткое множество Х – универсальное, если 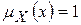 для каждого
для каждого 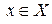 .
.
Пример 1. Пусть X = {Запорожец, Жигули, Мерседес, ...} – множество марок автомобилей, а Y = [0, µ) – универсальное множество "стоимость", тогда на Y мы можем определить нечеткие множества типа: "для бедных", "для среднего класса", "престижные", с функциями принадлежности типа:

Имея эти функции и зная стоимости автомобилей из X в данный момент времени, мы тем самым определим на X нечеткие множества с этими же названиями.
Так, например, нечеткое множество "для бедных", заданное на универсальном множестве X = {Запорожец, Жигули, Мерседес, ...} выглядит следующим образом:

Аналогично можно определить Нечеткое множество "скоростные", "средние", "тихоходные" и т.д.
Пример 2. Нечеткое множество «Оптимальный возраст работника».
E = [20, 70], функция принадлежности, полученная на основе опроса ряда экспертов:
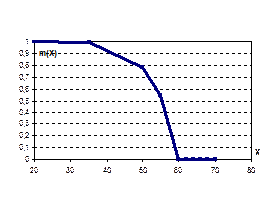
| Возраст от 20 до 35 оценивается экспертами как бесспорно оптимальный, в диапазоне от 35 до 60 эксперты проявляют неуверенность, от 60 до 70 – не оптимальный. |
Определение. Носителем нечетким множеством 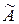 называется подмножество А множества Х, содержащее те элементы из Х, для которых значения функции принадлежности
называется подмножество А множества Х, содержащее те элементы из Х, для которых значения функции принадлежности 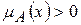 .
.
Следует заметить, что носитель нечеткого множества – это множество в обычном смысле.
Пример 3. Пусть Х – множество натуральных чисел. Тогда его нечеткое подмножество  очень малых чисел может быть таким:
очень малых чисел может быть таким:
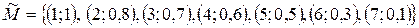 .
.
Носителем нечеткое множества  является множество
является множество  . Это обычное четкое подмножество множества Х.
. Это обычное четкое подмножество множества Х.
3.1.2. Основные операции над нечеткими множествами
Также как над четкими множествами определяются отношения включения, равенства, операции объединения, пересечения, дополнения и т.д., определяются они и над нечеткими множествами (далее НМ), только делается это при помощи функции принадлежности.
3.1.2.1. Нечеткое включение и нечеткое равенство множеств
Определение. Пусть заданы нечетких подмножеств  множества Х. Степень включения
множества Х. Степень включения 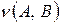 НМ А в НМ В находится по формуле
НМ А в НМ В находится по формуле  .
.
Если 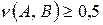 , то А нечетко включается в множество В и обозначается
, то А нечетко включается в множество В и обозначается 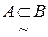 . Если
. Если 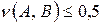 , то А нечетко не включается в множество В и обозначается
, то А нечетко не включается в множество В и обозначается  . Это понятие является обобщением понятия включения для четких множеств. Действительно, пусть А и В – четкие множества и
. Это понятие является обобщением понятия включения для четких множеств. Действительно, пусть А и В – четкие множества и 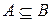 , отсюда следует
, отсюда следует 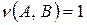 . Если же
. Если же 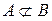 , то
, то 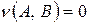
Определение. НМ A включается в НМ B – 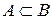 , если
, если  .
.
Иногда говорят, что B «доминирует» над А. Справедливо следующее утверждение: если НМ А включается в НМ В, то выполняется и нечеткое включение 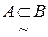 . Но, если же выполняется
. Но, если же выполняется 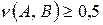 , то из этого не следует, что
, то из этого не следует, что 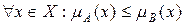 .
.
Определение. Степень равенства двух нечетких подмножеств  множества Х определяется как
множества Х определяется как 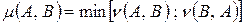 .
.
Если  , то множества нечетко равны
, то множества нечетко равны 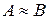 . Если
. Если 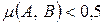 , то множества нечетко не равны
, то множества нечетко не равны 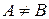 . Если
. Если 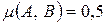 , то множества взаимно индифферентны
, то множества взаимно индифферентны  .
.
Понятия нечеткого равенства и неравенства, индифферентности являются обобщением понятий равенства и неравенства для четких множеств. Действительно, пусть А и В – четкие множества, тогда в случае А=В, 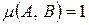 , если же А ≠ В и
, если же А ≠ В и 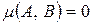 .
.
Определение. НМ Аравно НМ В – А=В, если 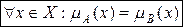 .
.
Нетрудно заметить, если выполняется равенство множеств А=В, то эти множества являются и нечетко равные 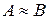 .
.
3.1.2.2. Теоретико-множественные операции
| Классическая теория множеств | Нечеткие множества |
Основные операции над четкими множествами:
Пересечение множеств 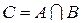 ;
Объединение множеств ;
Объединение множеств 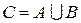 ;
Отрицание (дополнение) множества ;
Отрицание (дополнение) множества 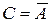 . .
| Заде предложил набор аналогичных операций над НМ через операции с функциями принадлежности:
Если А <=> mА(x), В <=> mВ(x), то результат операций – нечеткое множество С<=>mС(x), причем:
§ если С = А Ç В,тоmС(x) = min(mА(x), mВ(x));
§ если С = А È В,тоmС(x) = max(mА(x), mВ(x));
§ еслиС = 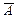 ,то mС(x) = 1 - mА(x). ,то mС(x) = 1 - mА(x).
|
Пример. Пусть A – нечеткое множество «от 5 до 8» и B – нечеткое множество «около 4», заданные своими функциями принадлежности:

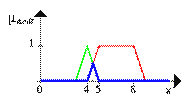
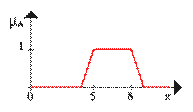 I)
I)

II) III)
I) Нечеткое множество «между 5 и 8» И (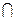 ) «около 4» (синяя линия).
) «около 4» (синяя линия).
II) Нечеткое множество «между 5 и 8» ИЛИ (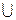 ) «около 4» (синяя линия).
) «около 4» (синяя линия).
III) Нечеткое множество НЕ A (синяя линия - это отрицание нечеткого множества A).
3.1.2.3. Свойства операций над нечеткими множествами
Пусть А, В, С – НМ, тогда выполняются следующие свойства:
1) Коммутативность: 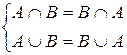 .
.
2) Ассоциативность: 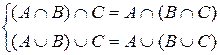 .
.
3) Идемпотентность: 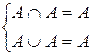 .
.
4) Дистрибутивность: 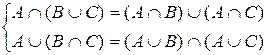 .
.
5) Законы де Моргана:  .
.
6) 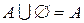
7)  .
.
8) 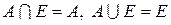 .
.
ЗАМЕЧАНИЕ: В отличие от четких множеств, для НМ в общем случае: 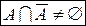 и
и 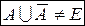 .
.
3.1.3. Дополнительные операции над нечеткими множествами
Определение. Результатом алгебраического произведения двух НМ A и B (обозначается A×B) является НМ с функцией принадлежности:
mA××B (x) = mA(x)×mB(x) "xÎX.
Определение. Результатом алгебраической суммы двух НМ A и B (обозначается A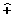 B) является НМ с функцией принадлежности:
B) является НМ с функцией принадлежности:
mA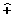 B(x)=m A(x) + mB(x)- mA(x)mB(x) "xÎX.
B(x)=m A(x) + mB(x)- mA(x)mB(x) "xÎX.
Для операций {×, 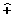 } выполняются свойства:
} выполняются свойства:

| – коммутативность |

| – ассоциативность |
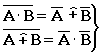
| – теоремы де Моргана |
A×Æ = Æ, A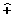 Æ = A, A×E = A, A
Æ = A, A×E = A, A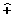 E = E
E = E
Не выполняются:
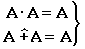
| – идемпотентность |

| – дистрибутивность |
A×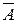 = Æ, A = Æ, A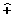  = E = E
|
Замечание: При совместном использовании операций {È, Ç, +, ×} выполняются свойства:
А×(BÈC) = (A×B)È(A × C);
А× (BÇC) = (A×B)Ç(A×C);
А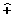 (BÈC) = (A
(BÈC) = (A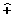 B)È(A
B)È(A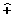 C);
C);
А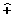 (BÇC)=(A
(BÇC)=(A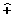 B)Ç(A
B)Ç(A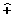 C).
C).
На основе операции алгебраического произведения (по крайней мере для целых a эта основа очевидна) определяется операция возведения в степень a нечеткого множества A, где a – положительное число. Нечеткое множество Aa определяется функцией принадлежности: 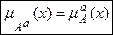 .
.
Частным случаем возведения в степень являются:
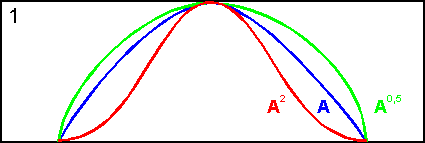
CON(A) = A2 – операция концентрирования,
DIL(A) = A0,5 – операция растяжения,
которые используются при работе с лингвистическими переменными.
Определение. Декартово произведение нечетких множеств: Пусть A1, A2, ... , An – нечеткие подмножества универсальных множеств E1, E2, ... , En соответственно. Декартово произведение A=A1´A2´ ...´An является нечетким подмножеством множества E=E1´E2´ ...´En с функцией принадлежности:
mA(x1, x2, ..., xn) = min{ mA1(x1), mA2(x2) , ... , mAn(xn) }.
Определение. Оператор увеличения нечеткости:Пусть A – НМ, E – универсальное множество и для всех xÎE определены нечеткие множества K(х). Совокупность всех K(х) называется ядром оператора увеличения нечеткости Ф. Результатом действия оператора Ф на НМ A является НМ вида:
Ф(A, K) = 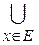 mA (x)×K(х), где mA(x)×K(х) – произведение числа на НМ.
mA (x)×K(х), где mA(x)×K(х) – произведение числа на НМ.
Используется для преобразования четких множеств в нечеткие и для увеличения нечеткости НМ.
Пример. E = {1, 2, 3, 4}; A = 0,8/1+0,6/2+0/3+0/4;
K(1)=1/1+0,4/2; K(2)=1/2+0,4/1+0,4/3; K(3)=1/3+0,5/4; K(4)=1/4.
Тогда Ф(A,K) = mA(1)×K(1)ÈmA(2)×K(2)ÈmA(3)×K(3)ÈmA(4)×K(4) =
= 0,8(1/1+0,4/2) È 0,6(1/2+0,4/1+0,4/3) =
= 0,8/1+0,6/2+0,24/3.
Определение. Четкое множество a-уровня: Множеством a-уровня НМ A универсального множества E называется четкое подмножество Aa универсального множества E, определяемое в виде:
Aa ={ x/m A(x)³ a }, где a £ 1.
Пример. A = 0,2/x1 + 0/x2 + 0,5/x3 + 1/x4 ,
тогда A0.3 = {x3, x4}; A0.7 = {x4}.
Достаточно очевидное свойство: если a1 ³ a2 , то Aa1 £ Aa2 .
Теорема о декомпозиции. Всякое нечеткое множество A разложимо по его множествам уровня в виде:
A =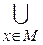 aAa, где aAa – произведение числа a на множество A, и a "пробегает" область значений M функции принадлежности НМ A.
aAa, где aAa – произведение числа a на множество A, и a "пробегает" область значений M функции принадлежности НМ A.
Пример. A = 0,1/x1 + 0/x2 + 0,7/x3 + 1/x4 представимо в виде:
A = 0,1(1,0,1,1) È 0,7(0,0,1,1,) È 1(0,0,0,1)=
= (0,1/x1+0/x2+0,1/x3+0,1/x4)È(0/x1+0/x2+0,7/x3+0,7/x4)È
È(0/x1+0/x2+0/x3+1/x4)=0,1/x1+0/x2+0,7/x3+1/x4.
3.2. Нечеткие отношения
3.2.1. Способы задания нечетких отношений
Определение. Нечетким отношением R на множествах X1, X2 … Xn называется нечеткое подмножество декартова произведения X1´X2´…´Xn. Степень принадлежности μR(x1,x2…xn) показывает степень выполнения отношения R между соответствующими элементами.
Примеры:
1). Пусть X и Y– множества всех действительных чисел. Нечеткое отношение R: X´Y®[0,1] – «x много больше y» можно задать функцией принадлежности:
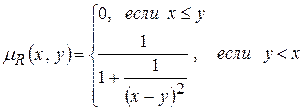
2). Нечеткое отношение R, для которого mR(x,y) = e-k(x-y)2, при достаточно больших k можно интерпретировать так: «x и y близкие друг к другу числа».
3). Нечеткое отношение R: X´Y®[0,1] – «x приблизительно равно y». Пусть  . Тогда нечеткое отношение удобно задавать матрицей вида:
. Тогда нечеткое отношение удобно задавать матрицей вида:
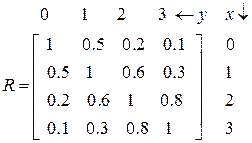
Замечание:В случае конечных или счетных универсальных множеств очевидна интерпретация нечеткого отношения в виде взвешенного графа, в котором пара вершин (xi,xj) в случае XRX соединяется ребром с весом μR(xi,xj), в случае XRY пара вершин (xi,yj) соединяется ребром с весом μR(xi,yj).
4). Пусть Х = {x1, x2, x3}, и задано нечеткое отношение R: X´X® [0,1], представимое графом:
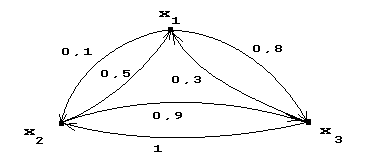
5). Пусть X = {x1, x2} и Y = {y1, y2, y3} и нечеткое отношение XRYзадает нечеткий граф вида:
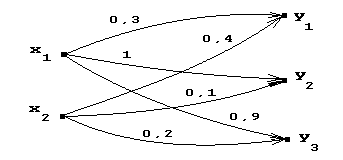
Определение. Носителем нечеткого отношения R называется обычное множество упорядоченных пар (x, y), для которых функция принадлежности положительна:
S(R) = {(x, y): mR(x, y) > 0}.
3.2.2. Основные операции над нечеткими отношениями
1) Объединение двух отношений R1 и R2.
Объединение двух нечетких отношений обозначается R1ÈR2 и определяется выражением:
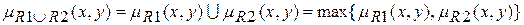
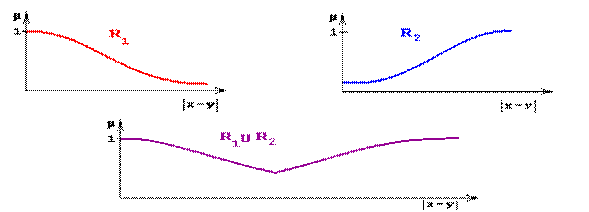
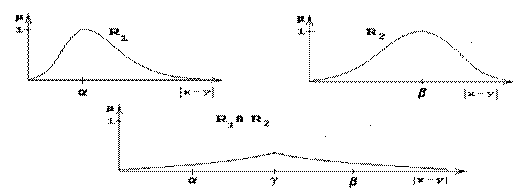
Пример. Ниже изображены отношения действительных чисел, содержательно означающие: xR1y – «числа x и y очень близкие», xR2y – «числа x и y очень различны" и их объединение xR1ÈR2y – «числа x и y очень близкие или очень различные».
Функции принадлежности отношений заданы на модуле разности |x-y|.
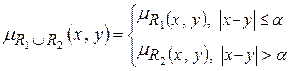 ,
,
где α – такое |x-y|, что μR1(x,y) = μR2(x,y).
2) Пересечение двух отношений R1 и R2.
Пересечение двух нечетких отношений R1и R2 обозначается R1ÇR2 и определяется выражением:
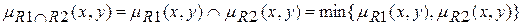
Пример.
3.2.2.1.Проекция нечеткого отношения
Пусть R – нечеткое отношение R: (x, y) ® [0,1]. Первой проекцией 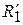 отношения R (проекция на X) называется нечеткое множество
отношения R (проекция на X) называется нечеткое множество 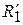 , заданное на множестве X, с функцией принадлежности:
, заданное на множестве X, с функцией принадлежности:  .
.
Аналогично, второй проекцией 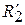 (проекцией на Y) называется нечеткое множество
(проекцией на Y) называется нечеткое множество 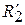 , заданное на множестве Y, с функцией принадлежности:
, заданное на множестве Y, с функцией принадлежности: 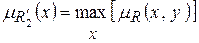 .
.
Вторая проекция первой проекции (или наоборот) называется глобальной проекцией нечеткого отношения и обозначается h(R). Таким образом, 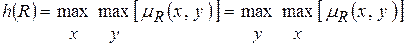 .
.
Если h(R)=1 – отношение нормально, если h(R)<1 – субнормально.
Пример:
| R | y1 | y2 | y3 | y4 | 1-я | |
| x1 | 0.1 | 0.2 | 0.3 | |||
| x2 | 0.6 | 0.8 | 0.1 | 0.8 | ||
| x3 | 0.3 | 0.6 | ||||
| x4 | 0.8 | 0.1 | ||||
| x5 | 0.9 | 0.7 | 0.5 | 0.9 | ||
| x6 | 0.9 | 0.3 | 0.7 | 0.9 | ||
| 2-я | 0.9 | 0.7 | h(R)=1 |
Проекции 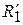 и
и 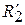 нечеткого отношения XRY в свою очередь определяют в X´Y нечеткие отношения
нечеткого отношения XRY в свою очередь определяют в X´Y нечеткие отношения 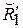 и
и 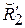 с функциями принадлежности:
с функциями принадлежности: 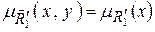 при любом y,
при любом y, 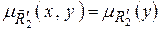 при любом x, называемые, соответственно, цилиндрическим продолжением
при любом x, называемые, соответственно, цилиндрическим продолжением 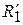 и цилиндрическим продолжением
и цилиндрическим продолжением 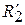 .
.
Замечание: Очевидно, что для любых нечетких подмножеств А и В, определенных, соответственно, на X и Y, можно построить их цилиндрические продолжения А и В.
Пример (продолжение):
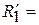
| 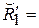
| y1 | y2 | y3 | y4 | |||
| x1 | x1 | |||||||
| x2 | 0.8 | x2 | 0.8 | 0.8 | 0.8 | 0.8 | ||
| x3 | x3 | |||||||
| x4 | x4 | |||||||
| x5 | 0.9 | x5 | 0.9 | 0.9 | 0.9 | 0.9 | ||
| x6 | 0.9 | x6 | 0.9 | 0.9 | 0.9 | 0.9 |
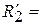
| 
| y1 | y2 | y3 | y4 | |||||
| x1 | 0.9 | 0.7 | ||||||||
| y1 | y2 | y3 | y4 | x2 | 0.9 | 0.7 | ||||
| 0.9 | 0.7 | x3 | 0.9 | 0.7 | ||||||
| x4 | 0.9 | 0.7 | ||||||||
| x5 | 0.9 | 0.7 | ||||||||
| x6 | 0.9 | 0.7 |
Нечеткое отношение XRY называется сепарабeльным, если оно равно пересечению цилиндрических продолжений своих проекций, т.е. если 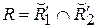 , т.е.
, т.е.  .
.
Замечание: Если определено декартово произведение нечетких множеств (выше оно введено), то, очевидно, нечеткое отношение XRY сепарабельно, если оно является декартовым произведением своих проекций, т.е. R=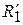 Ç
Ç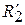 .
.
Пример (продолжение):

| y1 | y2 | Y3 | Y4 | ¹R | |
| x1 | 0.9 | 0.7 | ||||
| x2 | 0.8 | 0.8 | 0.8 | 0.7 | ||
| x3 | 0.9 | 0.7 | ||||
| x4 | 0.9 | 0.7 | ||||
| x5 | 0.9 | 0.9 | 0.9 | 0.7 | ||
| x6 | 0.9 | 0.9 | 0.9 | 0.7 |
т.е. исходное отношение R несепарабельно.
3.2.3. Композиция двух нечетких отношений
Большое значение в теории нечетких множеств имеет композиция (или произведение) нечетких отношений. В отличие от обычных (четких) отношений композицию (произведение) нечетких отношений можно определить разными способами.
Определение. ПустьR1 – нечеткое отношение R1: (X´Y) ® [0, 1] между X и Y, и R2 – нечеткое отношение R2: (Y´Z) ® [0, 1] между Y и Z. Нечеткое отношение между X и Z, обозначаемое R2·R1, определенное через R1 и R2 выражением: 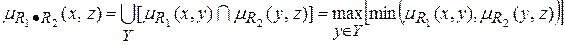 ,
,
называется (max-min)-композицией отношений R1 и R2.
Пример.
| R1 | R2 | R2·R1 | |||||||||||||
| y1 | y2 | y3 | z1 | z2 | z3 | z4 | z1 | z2 | z3 | z4 | |||||
| x1 | 0,1 | 0,7 | 0,4 | y1 | 0,9 | 0,2 | x1 | 0,3 | 0,6 | 0,1 | 0,7 | ||||
| x2 | 0,5 | y2 | 0,3 | 0,6 | 0,9 | x2 | 0,9 | 0,5 | 0,5 | ||||||
| y3 | 0,1 | 0,5 |
Операция (max-min)-композиции ассоциативна, т.е.
R3· (R2·R1) = (R3·R2 ) ·R1.
Операция (max-min)-композиции дистрибутивна относительно объединения, но не дистрибутивна относительно пересечения:
R3· (R2ÈR1) = (R3·R2)È(R3·R1),
R3· (R2ÇR1) ¹ (R3· R2)Ç(R3· R1).
Замечание:В выражении  для (max-min)-композиции операцию Ç можно заменить любой другой, для которой выполняются те же ограничения, что и для Ç: ассоциативность и монотонность по каждому аргументу.
для (max-min)-композиции операцию Ç можно заменить любой другой, для которой выполняются те же ограничения, что и для Ç: ассоциативность и монотонность по каждому аргументу.
Определение. ПустьR1 – нечеткое отношение R1: (X´Y) ® [0, 1] между X и Y, и R2 – нечеткое отношение R2: (Y´Z) ® [0, 1] между Y и Z. Нечеткое отношение между X и Z, обозначаемое R2*R1, определенное через R1 и R2 выражением: 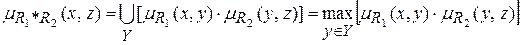 ,
,
называется (max-prod)-композицией отношений R1 и R2.
3.2.4. Условные нечеткие подмножества
Пусть X и Y – универсальные множества, взаимосвязь которых задана нечетким отношением R: (X´Y) ® [0, 1], т.е. для каждой пары (x, y)ÎX´Y задано значение функции принадлежности mR(x, y) Î [0, 1].
Пусть А – некоторое НМ, заданное на Х, т.е. определена функция принадлежности mA(x) для всех х из Х. Тогда НМ А и нечеткое отношение R индуцируют в Y нечеткое подмножество B (обозначение B=A·R) с функцией принадлежности 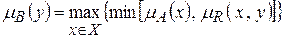 .
.
Пример:
Пусть X = {x1, x2, x3}, Y = {y1, y2, y3, y4} и заданы нечеткое множество A = {0,3/x1, 0,7/x2, 1/x3} и нечеткое отношение XRY:
| XRY = | y1 | y2 | y3 | y4 | |
| x1 | 0,8 | 0,3 | |||
| x2 | 0,8 | 0,3 | 0,8 | 0,2 | |
| x3 | 0,2 | 0,3 | 0,4 |
Проведем операцию «min» для А и столбца y1 :
| min | y1 | = | y1 | = | y1 | |||
| x1 | x2 | x3 | 0,8 | 0,3Ç0,8 | 0,3 | |||
| 0,3 | 0,7 | 0,8 | 0,7Ç0,8 | 0,7 | ||||
| 0,2 | 1Ç0,2 | 0,2 |
После выполнения операции «max» на элементах полученного столбца имеем: mB(y1) = 0,3È0,7È0,2 = 0,7.
Проделав аналогичные вычисления для y2, y3, y4 имеем:
mB(y2) = 0,3; mB(y3) = 0,7; mB(y4) = 0,4.
И окончательно:
| А | · | R | = | B | ||||||
| x1 | x2 | x3 | 0,8 | 0,3 | y1 | y2 | y3 | y4 | ||
| 0,3 | 0,7 | 0,8 | 0,3 | 0,8 | 0,2 | 0,7 | 0,3 | 0,7 | 0,4 | |
| 0,2 | 0,3 | 0,4 | ||||||||
| 0,8 | 0,3 |
Если
А1 индуцирует А2 посредством R1,
А2 индуцирует А3 посредством R2,
.............................................
Аn-1 индуцирует Аn посредством Rn-1,
то
А1 индуцирует Аn посредством Rn-1·Rn-2· ... ·R1,
где Rn-1·Rn-2· ... ·R1 – композиция нечетких отношений R1, R2, ..., Rn.
Пример:
Вернемся к примеру (max-min)-композиции.
| R1 | R2 | R2·R1 | |||||||||||||
| y1 | y2 | y3 | z1 | z2 | z3 | z4 | z1 | z2 | z3 | z4 | |||||
| x1 | 0,1 | 0,7 | 0,4 | y1 | 0,9 | 0,2 | x1 | 0,3 | 0,6 | 0,1 | 0,7 | ||||
| x2 | 0,5 | y2 | 0,3 | 0,6 | 0,9 | x2 | 0,9 | 0,5 | 0,5 | ||||||
| y3 | 0,1 | 0,5 |
Пусть А = {0,3/x1, 0,7/x2 }, тогда
| A1 | · | R1 | = | A2 | |||
| x1 | x2 | 0,1 | 0,7 | 0,4 | y1 | y2 | y3 |
| 0,3 | 0,7 | 0,5 | 0,7 | 0,5 | 0,3 |
| A2 | · | R2 | = | A3 | ||||||
| y1 | y2 | y3 | 0,9 | 0,2 | z1 | z2 | z3 | z4 | ||
| 0,7 | 0,5 | 0,3 | 0,3 | 0,6 | 0,9 | 0,7 | 0,5 | 0,7 | 0,5 | |
| 0,1 | 0,5 |
| A1 | · | R1· R2 | = | A3 | |||||
| x1 | x1 | 0,3 | 0,6 | 0,1 | 0,7 | z1 | z2 | z3 | z4 |
| 0,3 | 0,3 | 0,9 | 0,5 | 0,5 | 0,7 | 0,5 | 0,7 | 0,5 |
3.3. Нечеткая и лингвистическая переменные
Понятие нечеткой и лингвистической переменных используется при описании объектов и явлений с помощью нечетких множеств.
Определение. Нечеткая переменная характеризуется тройкой <α, X, A>, где
α – наименование переменной,
X – универсальное множество (область определения α),
A – нечеткое множество на X, описывающее ограничения (т.е. m A(x)) на значения нечеткой переменной a.
Определение. Лингвистической переменной называется набор <b ,T,X,G,M>, где
b – наименование лингвистической переменной;
Т – множество ее значений (терм-множество), представляющих собой наименования нечетких переменных, областью определения каждой из которых является множество X. Множество T называется базовым терм-множеством лингвистической переменной;
G – синтаксическая процедура, позволяющая оперировать элементами терм-множества T, в частности, генерировать новые термы (значения). Множество TÈG(T), где G(T) – множество сгенерированных термов, называется расширенным терм-множеством лингвистической переменной;
М – семантическая процедура, позволяющая превратить каждое новое значение лингвистической переменной, образуемое процедурой G, в нечеткую переменную, т.е. сформировать соответствующее НМ.
Пример. Рассмотрим лингвистическую переменную с именем b=«температура в комнате». Тогда оставшуюся четверку <T,X,G,M>, можно определить так:
1) универсальное множество 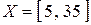 ;
;
2) терм-множество T = {"холодно", "комфортно", "жарко"} с такими функциями принадлежностями:  ;
; 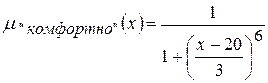 ;
; 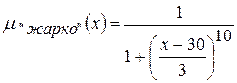 .
.
3) синтаксические правила G, порождающее новые термы с использованием связок "и", "или" и модификаторов типа "очень", "не", "более-менее" и других;
4) М будет являться процедурой, ставящей каждому новому терму в соответствие нечёткое множество из Х по правилам: если термы А и В имели функции принадлежности μА(x) и μB(x) соответственно, то новые термы будут иметь следующие функции принадлежности, заданные в таблице 3.1.
Таблица 3.1. Пример семантической процедуры
| Квантификатор | Функция принадлежности |
| не t | 
|
| очень t | 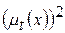
|
| более-менее t | 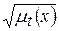
|
| А и В | min(μA(x),μB(x)) |
| А или В | max(μA(x),μB(x)) |
Графики функций принадлежности термов "холодно", "не очень холодно" и других термов лингвистической переменной "температура в комнате" показаны на рисунке 3.1.
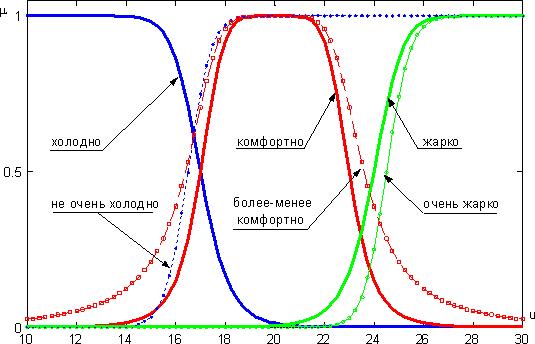
Рис. 3.1. Примеры термов лингвистической переменной "температура в комнате"
3.4. Нечеткие высказывания
3.4.1. Определение нечеткого высказывания
Определение. Нечеткие высказывания – конструкции следующего вида:
1) Высказывание <β есть β'>, где b – наименование лингвистической переменной, b'– ее значение, которому соответствует нечеткое множество на универсальном множестве Х.
Пример. Высказывание <давление большое> предполагает, что лингвистической переменной "давление" придается значение "большое", для которого на универсальном множестве Х переменной "давление" определено соответствующее данному значению "большое" нечеткое множество.
2) Высказывание <β есть mβ'>, где m – модификатор, которому соответствуют слова "ОЧЕНЬ", "БОЛЕЕ ИЛИ МЕНЕЕ", "МНОГО БОЛЬШЕ" и др.
Пример. <давление очень большое>, <скорость много больше средней> и др.
3) Составные высказывания, образованные из высказываний видов 1 и 2 и союзов "И", "ИЛИ", "ЕСЛИ.., ТО...", "ЕСЛИ.., ТО.., ИНАЧЕ".
3.4.1.1. Высказывания на множестве значений фиксированной лингвистической переменной
То, что значения фиксированной лингвистической переменной соответствуют нечетким множествам одного и того же универсального множества Х, позволяет отождествлять модификаторы "очень" или "не" с операциями "CON" и "дополнение", а союзы "И", "ИЛИ" с операциями "пересечение" и "объединение" над нечеткими множествами.
Пример. Лингвистическая переменная "толщина изделия" с базовым терм-множеством Т = {"малая", "средняя", "большая"}. При этом на Х=[10,80] определены нечеткие множества А1, А2, А3, соответствующие базовым значениям: "малая", "средняя", "большая".
В этом случае высказыванию <толщина изделия очень малая> соответствует НМ CONA = A2; высказыванию <толщина изделия не большая или средняя> – НМ 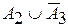 высказыванию <толщина изделия не малая и не большая> – НМ
высказыванию <толщина изделия не малая и не большая> – НМ 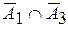 .
.
Высказывания <толщина изделия много больше средней> или <толщина изделия близка к средней> требуют использования нечетких отношений R («много больше, чем») и R («близко к»), заданных на Х´Х. Тогда этим высказываниям будут соответствовать нечеткие множества A·R1 и A·R2, индуцированные нечеткими отношениями R1 и R2.
3.4.1.2. Случай двух и более лингвистических переменных
Пусть <a, Ta, X, Ga, Ma> и <b, Tb, Y, Gb, Mb> – лингвистические переменные, и высказываниям <a есть a'>, <b есть b'> соответствуют нечеткие множества А и В, заданные на X и Y.
Составные нечеткие высказывания вида 3, связывающие значения лингвистических переменных a и b, можно привести к высказываниям вида 1, введя лингвистическую переменную (a, b), значениям которой будут соответствовать нечеткие множества на X´Y.
Напомним, что НМ А и В, заданные на X и Y, порождают на X´Y НМ 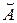 и
и  , называемые цилиндрическими продолжениями, с функциями принадлежности:
, называемые цилиндрическими продолжениями, с функциями принадлежности: 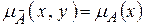 , при любых y,
, при любых y, 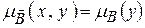 , при любых x, где (x,y) Î X´Y.
, при любых x, где (x,y) Î X´Y.
3.4.2. Правила преобразований нечетких высказываний
Нечеткие множества, соответствующие составным высказываниям <a есть a' и b есть b'> и <a есть a' или b есть b'>, определяются по следующим правилам (преобразования к виду 1), справедливым при условии невзаимодействия переменных, т.е. множества X и Y таковы, что их элементы не связаны какой-либо функциональной зависимостью.
3.4.2.1. Правило преобразования конъюнктивной формы
Справедливо выражение: <a есть a' и b есть b'> Þ <(a, b) есть (a'Çb')>. Здесь Þ – знак подстановки, a'Çb' – значение лингвистической переменной (a, b), соответствующее исходному высказыванию <a есть a' и b есть b'>, которому на X´Y ставится в соответствие НМ 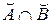 с функцией принадлежности:
с функцией принадлежности: 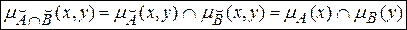 .
.
3.4.2.2. Правило преобразования дизъюнктивной формы
Справедливо выражение: <a есть a' или b есть b'> Þ <(a, b) есть (a'Èb')>, где значению (a'Èb') лингвистической переменной (a, b) соответствует НМ 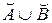 , с функцией принадлежности:
, с функцией принадлежности: 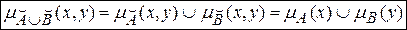 .
.
Замечание:Правила справедливы также для лингвистических переменных вида <a, T1, X, G1,M1> и <a, T2, Y, G2, M2>, когда в форме значений лингвистических переменных формализованы невзаимодействующие характеристики одного и того же объекта. Например, для построения НМ высказывания <ночь теплая и очень темная> нужно использовать правило конъюнктивной формы, а для высказывания <ночь теплая или очень темная> – правило дизъюнктивной формы.
3.4.2.3. Правило преобразования высказываний импликативной формы
Справедливо выражение: <если a есть a', то b есть b'> Þ<(a, b) есть (a'®b')>, где значению (a'®b') лингвистической переменной (a, b) соответствует нечеткое отношение XRY на X´Y. Функция принадлежности mR(x, y) зависит от выбранного способа задания нечеткой импликации.
3.4.3. Способы определения нечеткой импликации
Будем считать, что заданы универсальные множества X и Y, содержащие конечное число элементов. Под способом определения нечеткой импликации "если А, то В"(где А и В нечеткие множества на X и Y соответственно) будем понимать способ задания нечеткого отношения R на X´Y, соответствующего данному высказыванию. С целью обоснованного выбора определения нечеткой импликации, японскими математиками Мидзумото, Танака и Фуками было проведено исследование всех известных в литературе определений. Рассмотрим здесь наиболее распространенные определения, задающие следующие нечеткие отношения для высказывания "если А, то В":
1) R1: