Дисперсионный анализ

При исследовании однотипных величин возникают задачи их сравнения. Сравнение случайных величин производится путем сопоставления законов распределения или их моментов.

Законы распределения можно сопоставить на основе критерия Вилкоксона при нулевой гипотезе Н₀ о равенстве законов распределения двух случайных величин F_x=F_y и конкурирующей гипотезе Н₁ в виде:

F_x<F_y или F_x>F_y.

В этих случаях критическая область является односторонней. Поэтому нижнюю критическую точку и квантиль распределения находят при уровне значимости . Содержание остальных этапов проверки гипотез сохраняется. Следует отметить, принятие гипотезы Н₁ о том, что

F_x<F_y, означает X>Y.

Действительно, неравенство F_x(x)<F_y(x) равносильно неравенству

P(X<x)<P(Y<x),

следовательно, X>Y. Аналогично, если справедлива гипотеза F_x>F_y, то X<Y.

Вполне естественно сопоставление случайных величин на основе моментов проводить путем сравнения их математических ожиданий. Однофакторный дисперсионный анализ позволяет установить, оказывает ли существенное влияние некоторый фактор Ф, который имеет несколько уровней, на исследуемую случайную величину.

Задача сравнения выборок случайных величин формулируется следующим образом.

Имеются результаты наблюдений в виде совокупности слоев типа (6.1), задан уровень значимости a для проверки статистической гипотезы. В данном случае отдельные слои трактуются как выборки одной и той же случайной величины, полученные по результатам наблюдения за одним объектом при различных значениях фактора Ф (количество уровней фактора равно m).

Требуется проверить нулевую гипотезу Н₀ о равенстве математических ожиданий случайных величин всех выборок. Иначе говоря, требуется установить, значимо или незначимо различаются выборочные средние значения, вычисленные для каждого слоя.

Допущения: генеральные совокупности, соответствующие каждому слою, распределены нормально; дисперсии слоев одинаковы; математические ожидания, дисперсии, законы распределения случайных величин для различных слоев неизвестны, сами случайные величины являются непрерывными. Вполне понятно, что первые два условия являются наиболее существенными и весьма ограничивают область применения методов дисперсионного анализа.

Основная идея дисперсионного анализа состоит не в сопоставлении математических ожиданий случайных величин, а в сравнении оценки "факторной дисперсии", порождаемой воздействием фактора, и оценки "остаточной дисперсии", обусловленной случайными причинами. Если различие между этими оценками значимо, то фактор оказывает существенное влияние на случайную величину, в противном случае влияние фактора несущественно. Если установлено существенное влияние фактора, то каждому слою соответствует своя оценка математического ожидания. Упорядочение значений оценок математического ожидания позволит выявить влияние фактора.

Эту же задачу можно было бы решить путем проверки нулевой гипотезы о равенстве минимального и максимального значений оценок математического ожидания, вычисленных по всем слоям. Но такое сопоставление выборок игнорирует информацию, содержащуюся во всех слоях, кроме выбранных, и поэтому нецелесообразно.

Дисперсионный анализ выполняется поэтапно. Такими этапами являются следующие:

проверка выборок на принадлежность к нормальному закону распределения. Этап необходим, когда нет априорной информации о законах распределения слоев. Сущность такой проверки была рассмотрена в разделе 3 пособия. Если принадлежность нормальному закону не подтвердится, то аппарат дисперсионного анализа, вообще говоря, применять нельзя. Некоторые исследователи допускают его применение при больших объемах выборок (объем каждой выборки должен быть не менее 30) независимо от вида закона распределения;

проверка равенства оценок дисперсий во всех слоях выборки (проверка однородности дисперсий). Если однородность не подтвердится, то методы дисперсионного анализа не применимы;

вычисление оценки факторной и остаточной дисперсии;

сравнение средних значений величин методом дисперсионного анализа и формирование выводов по результатам сравнения.

Проверка однородности совокупности дисперсий

Для каждого слоя вычисляется несмещенная оценка дисперсии, обозначим эти оценки через σ₂(х), σ ₂(y), …, σ ₂(w) соответственно. Числа степеней свободы этих оценок

k₁=п₁–1, k₂=п₂–1, …, k_w = п_w–1.

Гипотеза Н₀ состоит в том, что выборки, по которым определены оценки дисперсии, получены из генеральных совокупностей, обладающих одинаковыми дисперсиями

σ ₂(x)= σ ₂(y)= … = σ ₂(w)= σ ₂,

при этом величина дисперсии σ ₂ остается неизвестной. Следует выяснить, являются ли величины σ ₂(х), σ ₂(y), …, σ ₂(w) оценками одной и той же генеральной дисперсии σ ₂.

Сравнение факторной и остаточной дисперсий

 

Пусть все выборки (6.1) характеризуют одну случайную величину Х при различных значениях фактора Ф, т.е. каждый слой соответствует одному количественному или качественному значению фактора. Сравнение дисперсий производится в следующем порядке:

рассчитывается среднее значение (оценка математического ожидания) по всей совокупности наблюдений , где п=п₁+п₂+…+п_т, а х_ij – j-й элемент i-го слоя;

вычисляются средние значения для всех слоев (групп)

, ;

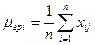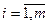определяется общая сумма квадратов отклонений наблюдаемых значений от оценки математического ожидания

; (6.7)

определяется факторная сумма квадратов отклонений средних по слоям от оценки математического ожидания (характеризует рассеяние между слоями)

; (6.8)

определяется остаточная сумма квадратов отклонений наблюдаемых значений внутри слоя от своей средней

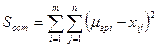(6.9)

Величина S_факт характеризует влияние фактора Ф. Это положение можно пояснить следующим образом. Пусть фактор оказывает существенное влияние на величину Х. Тогда результаты наблюдения для одного слоя, вообще говоря, отличаются от результатов, представленных в других слоях. Следовательно, различаются и средние значения по слоям, причем они тем больше отличаются от оценки математического ожидания по всей выборке, чем больше проявляется влияние фактора. Таким образом, сумма квадратов отклонений средних по слоям от общей средней и характеризует влияние фактора (возведение отклонений во вторую степень исключает взаимную компенсацию положительных и отрицательных отклонений).

Наблюдения внутри одного слоя различаются из-за воздействия случайных причин. Именно сумма квадратов отклонений наблюдаемых значений в каждом слое от среднего значения в слое и характеризует воздействие этих причин, т.е. величина S_ост отражает суммарное влияние случайных причин на значение величины Х.

Величина S_общ, как сумма квадратов отклонений конкретных значений от среднего значения, характеризует суммарное влияние фактора и случайных причин. Можно показать, что

S_общ=S_ост+S_факт,

тогда для вычисления остаточной суммы квадратов можно воспользоваться более простым соотношением

S_ост=S_общ–S_факт .

Разделив суммы квадратов отклонений на соответствующее число степеней свободы, получим оценки общей, факторной и остаточной дисперсий:

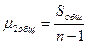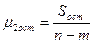; ; . (6.10)

Если средние значения случайной величины, вычисленные по отдельным выборкам одинаковы, то оценки факторной и остаточной дисперсий являются несмещенными оценками генеральной дисперсии и различаются несущественно. Тогда сопоставление оценок этих дисперсий по критерию Р. Фишера

F=_2факт/_2ост

должно показать, что нулевую гипотезу о равенстве факторной и остаточной дисперсий отвергнуть нет оснований. Если_2факт<_2ост, то нет необходимости прибегать к вычислению критерия Р. Фишера – из неравенства сразу следует вывод о выполнении нулевой гипотезы. Итак, из справедливости гипотезы о равенстве средних величин по группам следует соблюдение гипотезы о равенстве факторной и остаточной дисперсий.

Если нулевая гипотеза о равенстве средних величин по слоям является ложной, то с увеличением расхождения между слоями возрастает оценка факторной дисперсии, а вместе с ней и величина критерия F= σ _2факт/ σ _2ост . В результате значение F превысит критическое значение, и гипотеза о равенстве дисперсий будет отвергнута.

Рассуждая от противного, можно доказать справедливость утверждений: из справедливости (ложности) гипотезы о дисперсиях следует истинность (ложность) гипотезы о математических ожиданиях. Таким образом, вместо проверки нулевой гипотезы Н₀ о равенстве средних значений для совокупности выборок следует проверить гипотезу о равенстве факторной и остаточной дисперсий.

Существует несколько видов дисперсионного анализа. Нужный вариант выбирается с учетом числа факторов и имеющихся выборок из генеральной совокупности

Введение. Задачей дисперсионного анализа является исследование влияния различных факторов на изменчи­вость средних значений наблюдаемых случайных вели­чин. План дисперсионного анализа предполагает прове­дение эксперимента, позволяющее разложить сложную дисперсию на составляющие (при выполнении гипотезы об аддитивности дисперсий изучаемой случайной величи­ны). Далее полученные дисперсии оцениваются по опре­деленному критерию. Наиболее удобно и оправдано сравнивать полученные дисперсии с ошибкой опытных данных, которую получают по параллельным опытам на каждом (или на некоторых) уровне факторов.

1.1.1. Алгоритм однофакторного дисперсионного ана­лиза. Исходные данные. Необходимо выяснить влияние фактора А на выходную переменную у. Предполагается, что результаты наблюдений можно представить мо­делью

(1.1)

где 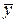– суммарный эффект во всех опытах (среднее зна­чение); –эффект фактора А на i-ом уровне; – ошибка измерения на i-ом уровне; т – число параллель­ных опытов; р – число уровней фактора А.

Очевидно, общее число опытов

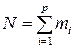(1.2)

или при одинаковом числе параллельных опытов

N=рт. (1.3)

Предполагается, что закон распределения случайной величины нормальный, а рассеяние опытов на каждом уровне фактора А не превышает некоторой величины или дисперсии на каждом уровне однородны.

План эксперимента и подготовительные расчеты пред­ставлены в табл. 1.1.

Таблица 1.1. Результаты расчетов при однофакторном дисперсионном анализе

План	Результаты расчетов
j i	Параллельные опыты 1,2, …,	Суммы результатов по параллельным опытам	Средний по параллельным опытам
Уровни (1) фактора А (2) . . . p	y11, y12,…,   y21, y22,…,   … , …   yp1, yp2,…,	. . .	. . .

 

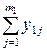
Расчет средних:

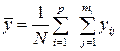– общее среднее; (1.4)

– среднее по уровням фактора А(строкам).(1.5)

Расчет чет сумм квадратов отклонений. Сумма квадратов отклонений, связанная с рассеиванием относительно общего среднего:

; (1.6)

сумма квадратов отклонений, связанная с рассеиванием между уровнями фактора А (междууровневая):

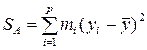; (1.7)

сумма квадратов отклонений, связанная с рассеиванием внутри выборки по уровням (внутриуровневая):

; (1.8)

сумма квадратов отклонений, свазанная с рассеиванием по параллельным опытам на i-ом уровне:

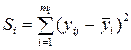. (1.9)

Расчет дисперсии. Рассчитанные суммы имеют соответственно следующие степени свободы f:

; (1.10)

; (1.11)

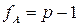; (1.12)

. (1.13)

Из условия (1.8)

,

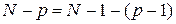т.е. получается тождество.

Рассчитаем дисперсии:

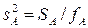– дисперсия фактора А; (1.14)

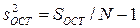– остаточная дисперсия; (1.15)

– ошибка опыта (дисперсия (1.16)

воспроизводимости);

– дисперсия параллельных (1.17)

опытов на i-ом уровне.

Проверка однородности дисперсий. Однородность дисперсий на каждом уровне фактора А можно проверить по критерию Кохрена, расчетное значение которого определяют по уравнению:

, (1.18)

где – максимальная из рассчитанных дисперсий параллельных опытов (построчных дисперсий, см. табл. 1.1); 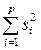– сумма всех дисперсий по уровням фактора А.

Если выполняется условие

, (1.19)

то гипотеза об однородности дисперсий правомерна. находят по таблице критерия Кохрена для степеней свободы (максимальная дисперсия), 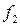(число уров­ней) и заданного уровня значимости q. В технических расчетах принят 5%-ный уровень значимости.

Оценка различия дисперсий. Строится отношение ди­сперсий фактора А к ошибке опыта и получается расчет­ное значение критерия Фишера: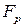

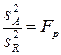. (1.20)

Принятие решений. Если расчетное значение крите­рия Фишера

(1.21)

 

(– табличное значение критерия Фишера для степе­ней свободы , 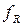и заданного уровня значимости q), то влияние уровней фактора А существенно. Условие (1.20) означает, что влияние фактора А, разделенного по уров­ням, превышает уровень ошибки опытных данных.

Результаты однофакторного дисперсионного анализа удобно представить в виде табл. 1.2, где расчет произво­дился по преобразованным формулам (1.6), (1.7) и (1.8).

1.1.2. Алгоритм двухфакторного дисперсионного ана­лиза. Исходные данные. Необходимо выяснить влияние двух факторов на некоторую выходную переменную (функцию отклика). Предполагается, что исследуется влияние факторов А и В, варьируемых на р- и k-ом уров­нях соответственно. Математическая модель эксперимен­та следующая:

. (1.22)

гдеи – эффекты факторов А и В соответственно на i-ом и j-ом уровнях; 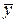– суммарный эффект факторов во всех опытах; – ошибка измерения (помеха), имею­щая нормальное распределение, нулевое математическое ожидание и определенную дисперсию. Общее число опы­тов при однократных наблюдениях

. (1.23)

Таблица 1.2. Результаты расчетов при однофакторном дисперсионном анализе

Источник изменчивости	Расчетные формулы и значения
S	j
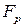
Между уровнями фактора
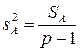
Внутри уровней фактора

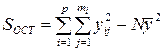
План эксперимента и некоторые расчеты сумм и средних представлены в табл. 1.3.

Таблица 1.3. План эксперимента и расчеты при двухфакторном дисперсионном анализе

j i	Уровни фактора В 1, 2, …, k	Средние по строкам
Уровни фактора А . . . p	y11, y12, …, y1k y21, y22, …, y2k . . . . . … . . . … . yp1, yp2, …, ypk	. . .
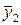Средние по столбцам	, , 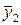…,	Общее среднее

Расчет средних. Можно получить следующие выборочные средние:

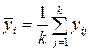– среднее по строкам; (1.24)

– среднее по столбцам; (1.25)

– общее среднее. (1.26)

Расчет сумм квадратов отклонений:

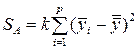; (1.27)

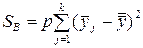; (1.28)

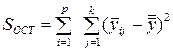; (1.29)

. (1.30)

Расчет дисперсий. Рассчитанные суммы имеют следующие степени свободы:

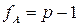; (1.31)

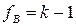; (1.32)

. (1.33)

Тогда дисперсии можно рассчитывать по формулам:

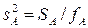; (1.34)

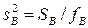; (1.35)

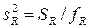. (1.36)

Оценка отношений дисперсий. Строятся отношения дисперсий факторов А и В к ошибке опыта и получаются расчетные значения критерия Фишера:

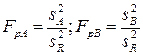. (1.37)

Принятие решений. Если расчетные значения крите­рия Фишера

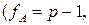или или

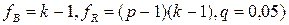, (1.38)

(– табличное значение критерия Фишера для степе­ней свободы или и заданного уровня значимости q), то влияние факторов A и В на выходную переменную су­щественно (при выбранных р- и k-ом уровнях).

Результаты и расчеты двухфакторного дисперсионно­го анализа удобно представить в виде табл. 1.4.

Примечание. Линейная модель (1.22) справедлива, если между факторами А и В отсутствует взаимодейст­вие, т. е. дисперсия. Если такое взаимодействие имеется, то входит в дисперсию ошибки опыта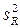и выделить ее можно только при наличии параллельных опытов по уровням факторов А и В. Такой алгоритм хотя принципиально и не отличается от приведенного выше, но имеет особенности.

1.1.3. Алгоритм дисперсионного анализа при исполь­зовании схемы латинского квадрата. Введение. В преды­дущих алгоритмах число необходимых опытов определя­лось произведением уровней исследуемых факторов. Ес­ли предположить, что число уровней одинаково, то в двухфакторном дисперсионном анализе необходимо про­вести N=р² (при р=k) опытов. Все возможные сочета­ния уровней и факторов дают так называемый полный факторный эксперимент (ПФЭ). Так, для двухфакторного дисперсионного анализа ДА на трех уровнях ПФЭ дает N=3²=9 опытов, для трехфакторного ДА на трех уровнях ПФЭ дает N=3³=27 опытов п т. д.

Возможно сокращение количества опытов и использование дробного факторного эксперимента (ДФЭ). Количество опытов в дисперсионном анализе сокращается в 1/p раз, если использовать в плане эксперимента латинский квадрат. Так, трехфакторный ДА по плану ДФЭ даст всего 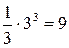опытов.

Таблица 1.4. Результаты расчетов при двухфакторном дисперсионном анализе

Источник изменчивости	Расчетные формулы и значения
S	j
Фактор А
Фактор В
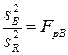
Ошибка опыта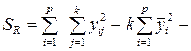

 

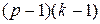
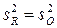
Определение. Латинским квадратом называется такая квадратная матрица р×р из р элементов, что каждый из элементов встречается в каждой строке и каждом столбце только один раз.

Из трех элементов образуется латинский квадрат 3×3:

ABC 123

BCA или 231; (1.39)

CAB 312

Из четырех элементов – латинский квадрат 4×4:

ABCD 1234

BCDA или 2341 (1.40)

CDAB 3412

DABC 4123.

В дисперсионном анализе используются стандартные латинские квадраты [см. формулы (1.39), (1.40)], у ко­торых первая строка и первый столбец построены в ал­фавитном порядке (элементы – буквы) или в порядке натурального ряда (элементы – цифры). Способ построе­ния таких квадратов – одношаговая циклическая пере­становка.

Применение. К планированию эксперимента по схеме дисперсионного анализа с латинским квадратом прибе­гают обычно при исследовании влияния на процесс трех дискретно-меняющихся факторов А, В, С. При этом фак­торы А и В могут быть связаны с переменными, а фак­тор С – с помехами.

Исходные данные. Необходимо выяснить влияние трех источников изменчивости – факторов А, В, С: фак­тор А – строка плана, фактор В – столбец плана, фак­тор С – элемент плана. Результаты эксперимента мож­но представить моделью

, (1.41)

в которой имеются кроме линейных эффектов еще три парных эффекта и один тройной эффект взаимодействия факторов; – ошибка с нормальным распределением. Если предположить, что взаимодействия факторов незна­чимы, то результаты эксперимента можно представить моделью

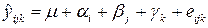. (1.42)

где 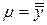– общий эффект во всех опытах; - эффект фактора А (строки); 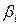– эффект фактора В (столбца); – эффект фактора С (элемента квадрата).

План эксперимента без повторных опытов представлен в табл. 1.5.

Расчет итогов по строкам , столбцам 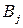и элементам квадрата :

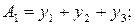
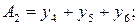
(1.43)

Таблица 1.5. Трехуровневый латинский квадрат

Фактор А	Фактор В	Итоги по строкам
b1	b2	b3
a1	c1 y1	c2 y2	c3 y3	A1
a2	c2 y4	c3 y5	c1 y6	A2
a3	c3 y7	c1 y8	c2 y9	A3
Итоги по столбцам	B1	B2	B3	Общий итог

 

; ; ; (1.44)

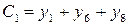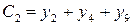; ; ; (1.45)

Расчет суммы квадратов всех наблюдений:

. (1.46)

Расчет суммы квадратов итогов по строкам, столбцам и элементам квадрата, деленных на соответствующее число элементов:

; (1.47)

; (1.48)

; (1.49)

Расчет корректирующего члена, равного квадрату общего итога, деленное на общее число опытов:

. (1.50)

Расчет сумм квадратов:

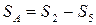– для строки; (1.51)

– для столбца; (1.52)

– для элементов квадрата; (1.53)

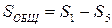– общая; (1.54)

– остаточная. (1.55)

Расчет дисперсий:

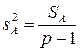– фактор А; (1.56)

– фактора В; (1.57)

– фактора С; (1.58)

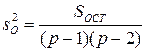– ошибка опыта. (1.59)

Оценка дисперсий осуществляется по критерию Фишера. Составляются дисперсионные отношения (расчетные)

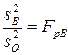, , . (1.60)

Принятие решения. Если расчетные значения критерия Фишера удовлетворяют неравенствам

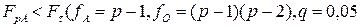; (1.61)

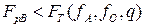; (1.62)

, (1.63)

то влияние всех факторов несущественно.

Если какое-нибудь из отношений (1.60) оказывается большим , то влияние этого фактора существенно.

Примечание. Для четырех факторов используется дисперсионный анализ по схеме греко-латинского квадрата, при большем числе уровней – гипергреко-латинские квадраты и латинские кубы.

 

В программе Excel предусмотрено проведение однофакторного дисперсионного анализа, двухфакторного дисперсионнного анализа без повторений, двухфакторного дисперсионнного анализа с повторениями (рис.40).

Рис. 40