рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Философия
- /
- Подходящий закон распределения
Реферат Курсовая Конспект
Подходящий закон распределения
Подходящий закон распределения - раздел Философия, Эмпирические распределения случайной величины 1. На Рис. 5. Изображен График Закона Распределения Для Данной Выборки. Этот ...
1. На рис. 5. изображен график закона распределения для данной выборки. Этот график больше всего похож на кривую нормального закона распределения, которая имеет симметричный холмообразный вид [2, c.117].
2. Для нормального закона распределения характерны следующие равенства:
1) 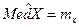
2) 
3) 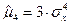
Проверим выполнение этих равенств для выборки  .
.
1) 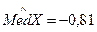 ,
, 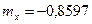 , следовательно,
, следовательно, 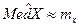
2) 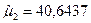 ,
, 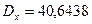 ,
, 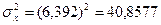 , следовательно,
, следовательно, 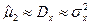
3) 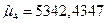 ,
, 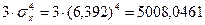 , следовательно,
, следовательно, 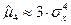
Характерные для нормального распределения равенства выполняются.
3. Для симметричного закона распределения, а нормальный закон распределения – это симметричный закон, необходимо выполнение следующих равенств: 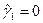 ,
, 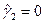 , т.е. равенство нулю несмещенных оценок коэффициента асимметрии и коэффициента эксцесса.
, т.е. равенство нулю несмещенных оценок коэффициента асимметрии и коэффициента эксцесса.
Проверим выполнение этих равенств для выборки  :
:
 , следовательно,
, следовательно, 
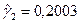 , следовательно,
, следовательно, 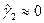
Характерные для симметричного закона распределения равенства выполняются.
4. Правило трех сигм: если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратичного отклонения.

Проверим выполнение этого правила для нашей выборки.
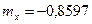
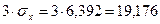
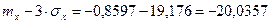
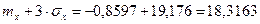
Все элементы выборки входят в отрезок  , т.е. условие, указанное в правиле трех сигм, выполняется, значит есть основание предполагать, что изучаемая величина распределена нормально.
, т.е. условие, указанное в правиле трех сигм, выполняется, значит есть основание предполагать, что изучаемая величина распределена нормально.
6.2 Критерий Пирсона 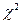
Критерий согласия - критерий проверки гипотезы о предполагаемом законе неизвестного распределения.
Существует несколько критериев согласия: 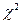 К. Пирсона, Колмогорова, критерий
К. Пирсона, Колмогорова, критерий 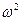 , Смирнова и т.д. Сначала рассмотрим критерий Пирсона – критерий
, Смирнова и т.д. Сначала рассмотрим критерий Пирсона – критерий 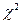 .
.
Критерий Пирсона отвечает на вопрос о том, случайно ли расхождение частот. Правда, как и любой критерий, он не доказывает справедливость гипотезы, а лишь устанавливает на принятом уровне значимости е согласие или несогласие с данными наблюдений.
Прежде чем проверять гипотезу о выбранном законе распределения, сначала необходимо выдвинуть эту гипотезу (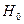 ) и конкурирующую ей (
) и конкурирующую ей (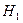 ):
):
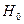 : случайная величина подчиняется нормальному закону распределения
: случайная величина подчиняется нормальному закону распределения
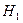 : случайная величина подчиняется другому закону распределения
: случайная величина подчиняется другому закону распределения
Для применения критерия Пирсона воспользуемся интервалами построенными ранее (таблица 4), но так как не в каждый интервал гистограммы попадает более пяти данных (интервалы 1,6,7, здесь  , см. таблицу 4), то для применения этого критерия объединим соседние столбцы гистограммы, т.е. объединяем 1,2 интервалы и 6,7 интервалы.
, см. таблицу 4), то для применения этого критерия объединим соседние столбцы гистограммы, т.е. объединяем 1,2 интервалы и 6,7 интервалы.
Для каждого интервала вычислим теоретическую вероятность попадания случайной величины в i-ый интервал гистограммы, при условии, что гипотеза 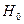 справедлива:
справедлива:  ,
,
Для каждого интервала вычислим теоретическое количество точек, попадающих в i-ый интервал: 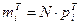 .
.
Для каждого интервала находим меру близости теоретических и практических данных i-ого интервала 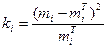
Вычислим общую меру близости:  , где r – число интервалов на гистограмме.
, где r – число интервалов на гистограмме.
Перед тем как считать теоретическую вероятность попадания случайной величины в i-ый интервал гистограммы  , необходимо нормировать случайную величину
, необходимо нормировать случайную величину 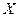 , т.е. вычислить значения
, т.е. вычислить значения  и
и 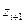 , причем наименьшее значение
, причем наименьшее значение 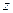 положим равным
положим равным 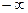 , а наибольшее -
, а наибольшее -  . Следует также напомнить значения, необходимые для вычисления
. Следует также напомнить значения, необходимые для вычисления 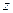 :
: 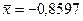 ,
, 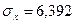 . Вычисление данных значений приводится в таблице 6.
. Вычисление данных значений приводится в таблице 6.
Результаты вычислений представлены в таблице 7.
Таблица 6
Нормирование случайной величины
| № | 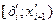
| 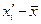
| 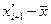
| 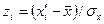
| 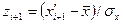
|
(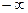 ; -6,8542) ; -6,8542)
| 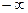
| -5,9945 | 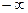
| -0,9378 | |
| [-6,8542; -2,1713) | -5,9945 | -1,3116 | -0,9378 | -0,2052 | |
| [-2,1713; 2,5116) | -1,3116 | 3,3713 | -0,2052 | 0,5274 | |
| [2,5116; 7,1945) | 3,3713 | 8,0542 | 0,5274 | 1,26 | |
[7,1945;  ) )
| 8,0542 | 
| 1,26 | 
|
Таблица 7
Результаты вычислений для критерия Пирсона
| № | 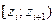
| 
| 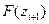
| 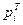
| 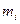
| 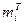
| 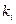
|
(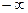 ; -0,9378) ; -0,9378)
| 0,1741 | 0,1741 | 16,5395 | 0,0176 | |||
| [-0,9378; -0,2052) | 0,1741 | 0,4189 | 0,2448 | 23,256 | 0,7789 | ||
| [-0,2052; 0,5274) | 0,4189 | 0,7009 | 0,282 | 26,79 | 3,8911 | ||
| [0,5274; 1,26) | 0,7009 | 0,8962 | 0,1953 | 18,5535 | 0,6806 | ||
[1,26;  ) )
| 0,8962 | 0,1038 | 9,861 | 0,3512 | |||
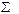
| 5,7194 |
Значит 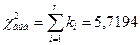
Найдем число степеней свободы распределения 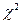 :
:  , где
, где  - количество интервалов ,
- количество интервалов , 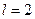 – число параметров предполагаемого закона распределения. Получим
– число параметров предполагаемого закона распределения. Получим 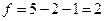
По таблице процентных точек распределения 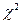 [1] находим критические значения
[1] находим критические значения 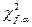 при
при 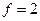 для уровней значимости
для уровней значимости  = 0,01; 0,05; 0,1:
= 0,01; 0,05; 0,1:
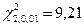
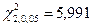
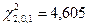
Поскольку 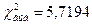 меньше критических значений
меньше критических значений 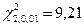 ,
, 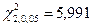 , то для уровней значимости
, то для уровней значимости  = 0,01; 0,05, согласно критерию Пирсона, нет оснований отвергнуть нулевую гипотезу. Так как
= 0,01; 0,05, согласно критерию Пирсона, нет оснований отвергнуть нулевую гипотезу. Так как 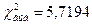 больше критического значения
больше критического значения 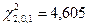 , то для уровня значимости
, то для уровня значимости  = 0,1 нулевая гипотеза отвергается.
= 0,1 нулевая гипотеза отвергается.
– Конец работы –
Эта тема принадлежит разделу:
Эмпирические распределения случайной величины
Предположение о виде закона распределения о РВЗ... На данном этапе анализа исходных данных по эмпирической функции распределения...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Подходящий закон распределения
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов