Расчетный метод.

Метод частных производных. Этот метод предполагает наличие аналитического выражения, связывающего выходной параметр с производственными погрешностями. Разложив уравнение (4) в ряд Тэйлора (ограничиваясь членами первого порядка малости), вычитая из него выходной параметр, переходя к конечным приращениям и деля полученное выражение на исходное для выходного параметра, получим:

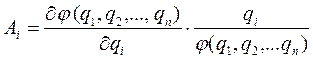(10)

Таким образом, имея аналитическое выражение выходного параметра функционального узла и произведя его дифференцирование, можно получить уравнение погрешности этого параметра с вполне определенными значениями коэффициентов влияния.

Определять коэффициенты влияния методом дифференцирования сложно и трудоемко. Вывод уравнения погрешности выходного параметра функционального узла, содержащего 6÷10 деталей, связан с достаточно громоздкими преобразованиями и вычислениями.

Метод раздельного дифференцирования. Этот метод, так же как и метод частных производных, предполагает наличие аналитического выражения выходного параметра узла как функция параметров схемных элементов, но имеет бесспорные преимущества в простоте определения коэффициентов влияния. Пользуясь этим методом, можно, не прибегая к нахождению частных производных, определять коэффициенты влияния в уравнениях погрешности выходного параметра по определенным правилам, которые легко доказываются, если взять полный дифференциал заданной функции выходного параметра и разделить его на исходное выражение.

Примеры.

1. Выходной параметр функционального узла выражен через произведение (отношение) параметров схемных элементов. Коэффициенты влияния в уравнениях погрешности выходного параметра равны показателям степени соответствующих параметров

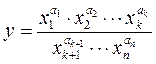, тогда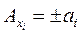

2. Выходной параметр функционального узла является алгебраической суммой ряда слагаемых вида:

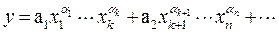
Коэффициенты влияния будут равны отношению соответствующего слагаемого, умноженного на показатель степени при нем, к величине выходного параметра y, т.е.

,

где 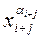- последний множитель, входящий в слагаемое, содержащее данный аргумент.

3. Выходной параметр функционального узла представлен многочленом вида

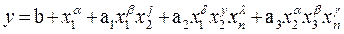
где 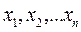- аргументы функции y;

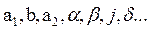и т.д. - любые числа.

Коэффициенты влияния будут равны отношению суммы членов, содержащих данный параметр, умноженный на показатели степени при них (со своими знаками) к выходному параметру y:

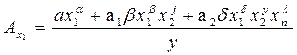
4. Выходной параметр функционального узла представляет собой логарифмическую функцию аргумента x, т.е.

,

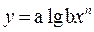Коэффициент влияния погрешности параметра x определяется как отношение произведения коэффициента на показатель степени n к выходному параметру, т.е.

.

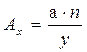5. Выходной параметр функционального узла является показательной функцией аргумента x , т.е.

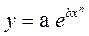
где a, b, n – любые числа.

Коэффициент влияния при в уравнении погрешности будет равен произведению только показателя степени bxⁿ на показатель степени n, т.е.

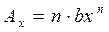
6. Выходной параметр функционального узла имеет вид

.

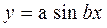Коэффициент влияния параметра x будет равен произведению полного аргумента bx на котангенс аргумента, т.е.

.

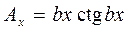7. Выходной параметр функционального узла задан в виде

.

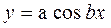Коэффициент влияния параметра x будет равен произведению полного аргумента, взятого с минусом, на тангенс аргумента, т.е.

.

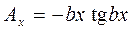В таблице приведены наиболее часто встречающиеся случаи задания функции (выходного параметра) и соответствующие им формулы для определения коэффициентов влияния уравнения погрешности

Заданная функция (выходной параметр в виде)	Формула для определения коэффициента влияния

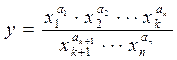
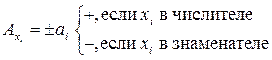
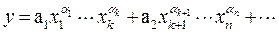
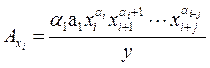
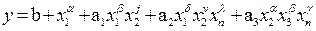
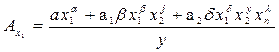
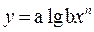
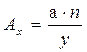
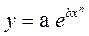
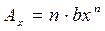
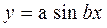
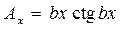
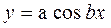
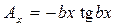
Выходной параметр функционального узла в общем случае может быть выражен произвольной функцией. Тогда для определения коэффициентов влияния следует произвести разложение этой функции на более простые, для которых справедливы соотношения, приведенные в таблице, и по ним вычислять коэффициенты влияния.