рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Философия
- /
- ТЕОРЕТИЧЕСКАЯ МЕХАНИКА- краткий курс КОНСПЕКТ ЛЕКЦИЙ ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ
Реферат Курсовая Конспект
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА- краткий курс КОНСПЕКТ ЛЕКЦИЙ ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА- краткий курс КОНСПЕКТ ЛЕКЦИЙ ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ - раздел Философия, Министерство Образования И Науки Российской Федерации...
Министерство образования и науки российской федерации
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
«МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ»
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА- краткий курс
КОНСПЕКТ ЛЕКЦИЙ
ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ
Направление подготовки 280700 – Техносферная безопасность
Профиль подготовки Инженерная защита окружающей среды
Квалификация (степень) выпускника бакалавр _
Форма обучения очная ________________________
Составители: проф. В.И.Антонов,
доц. И.М.Закалюкина
г. Москва
2012г.
ЛЕКЦИИ 1-2
Основные понятия механики
Теоретическая механика представляет собой науку об общих законах механического движения и механического взаимодействия материальных тел.
В теоретической механике изучается одна из форм движения материи – механическое движение, состоящее в том, что тело с течением времени изменяет свое положение в пространстве по отношению к другим телам. Механическим называют тот вид взаимодействия тел, в результате которого происходит изменение их движения или изменение их формы (деформация).
При исследовании движения какого-либо тела необходимо указать другое тело (тело отсчёта), по отношению к которому рассматривается движение. С телом отсчёта жёстко связывают систему координат. Тело отсчёта, связанная с ним система координат и счётчик времени (часы) образуют систему отсчёта.

|
| Рис.1.1 |
Фундаментальным понятием механики является сила, которая представляет собой количественную меру механического взаимодействия материальных тел. Сила – величина векторная. Ее действие на тело определяется численным значением или модулем силы, направлением действия и точкой приложения (Рис.1.1). Прямая, вдоль которой направлена сила, называется линией действия силы. Единицей измерения силы в системе СИ является ньютон (Н).
Кроме внешних воздействий, т.е. сил, характер движения любого тела определяется его инертностью, которая является одним из основных свойств движущейся материи. Это свойство проявляется в способности тела сохранять свое движение при отсутствии сил и изменять его под действием сил не мгновенно, а постепенно, тем медленнее, чем больше вещества содержится в теле. Одной из важнейших количественных характеристик инертности (инерции) тела является масса.
Модели материальных тел
Теоретическая механика является естественной наукой, опирающейся на результаты опыта и наблюдений и использующей математический аппарат при анализе результатов этих наблюдений. Изучая какое-либо явление, мы не можем охватить его во всем многообразии. Отвлекаясь при изучении механического движения материальных тел от всего частного, менее существенного, второстепенного и учитывая только те свойства, которые в данной задаче являются определяющими, мы приходим к рассмотрению различных моделей материальных тел, представляющих собой ту или иную степень абстракции.
Дадим определения основных моделей, используемых в теоретической механике.
1. Материальное тело, размерами и различием в движении отдельных точек которого можно пренебречь в рамках рассматриваемой задачи, называется материальной точкой.
Любое множество взаимодействующих материальных точек называется механической системой.
3. Если расстояние между любыми двумя точками тела не изменяется при любых механических взаимодействиях, то такое тело называется абсолютно твёрдым.
Правильный выбор модели во многом определяет успех решения поставленной задачи. Заметим, что среди перечисленных моделей наиболее общей, можно сказать всеобъемлющей, является модель механической системы. Следовательно, и все закономерности движения, установленные на основе этой модели, являются наиболее общими. Всякая попытка конкретизации свойств механической системы, учёт особенностей той или иной среды (жидкости, газа, упругого тела и т.д.) приводит, как правило, к столь большому росту объёма информации, что возникает необходимость специализации, возникают новые науки (теория упругости, гидродинамика. аэродинамика и т.д.).
Основные законы механики
Аксиома 1 Существует система отсчёта, по отношению к которой материальная точка…Аксиома 3
Аксиома 4(Принцип независимости действия сил.) Если на материальную точку действует одновременно несколько сил, то ускорение точки складывается из ускорений, которые…Координатный способ задания движения точки
Движение точки по отношению к выбранной системе отсчёта считается заданным, если известен способ, при помощи которого можно определить положение точки в любой момент времени.
|
| Рис.1.3 |
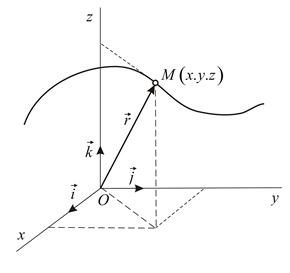
Положение точки 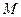 в системе отсчёта полностью определяется её координатами. Если известна зависимость координат от времени, движение точки считается заданным. В зависимости от содержания решаемой задачи можно использовать любую систему координат (декартову, цилиндрическую, сферическую и т.д.), наиболее целесообразную для данной задачи. Мы, в основном, будем использовать прямоугольную декартову систему координат., в которой законы движения точки имеют вид:
в системе отсчёта полностью определяется её координатами. Если известна зависимость координат от времени, движение точки считается заданным. В зависимости от содержания решаемой задачи можно использовать любую систему координат (декартову, цилиндрическую, сферическую и т.д.), наиболее целесообразную для данной задачи. Мы, в основном, будем использовать прямоугольную декартову систему координат., в которой законы движения точки имеют вид:
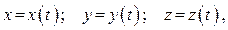 (1.1)
(1.1)
где  – время.
– время.
Вектор 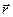 , проведённый из начала координат в точку
, проведённый из начала координат в точку 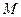 , называется радиусом–вектором точки. Координаты точки
, называется радиусом–вектором точки. Координаты точки 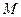 одновременно являются проекциями радиуса–вектора на координатные оси (Рис.1.3):
одновременно являются проекциями радиуса–вектора на координатные оси (Рис.1.3):
 (1.2)
(1.2)
где  – единичные векторы (орты) координатных осей.
– единичные векторы (орты) координатных осей.
Задавая координаты точки, мы тем самым задаем ее радиус-вектор. Наоборот, если задан радиус-вектор, то раскладывая этот вектор по координатным осям, определяем координаты точки. Иногда говорят о векторном способе задания движения точки, предполагая при этом, что радиус-вектор задается как функция времени. Такой способ удобен для решения ряда теоретических вопросов, поскольку он компактен и не связан с выбором конкретной системы координат. Но при решении практических задач необходимо переходить к тому или иному координатному способу задания движения точки.
Непрерывная кривая, которую описывает точка при своем движении, называется траекторией точки.
Скорость точки
Быстроту движения точки характеризует ее скорость, к определению которой мы сейчас переходим. Пусть в момент времени точка находится в положении ,… определяется радиусом–вектором , а в момент переходит в положение ,… Скоростью точки в данный момент времени называется предел отношения вектора перемещения к промежутку времени, за…Ускорение точки
Быстроту изменения вектора скорости характеризует ускорение точки. Пусть в момент времени точка находится в положении и имеет скорость , а в момент… Ускорением точки называется предел отношения приращения вектора скорости к… (1.6)Естественный способ задания движения точки
|
| Рис.1.6 |
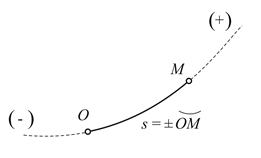
Пусть траектория точки 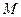 заранее известна. Рассматривая траекторию как криволинейную координатную ось, примем любую точку
заранее известна. Рассматривая траекторию как криволинейную координатную ось, примем любую точку 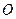 траектории за начало отсчета и установим положительное и отрицательное направления отсчета. Положение точки
траектории за начало отсчета и установим положительное и отрицательное направления отсчета. Положение точки 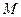 однозначно определяется дуговой координатой, которая равна взятой с соответствующим знаком длине дуги траектории, отделяющей в данный момент времени точку
однозначно определяется дуговой координатой, которая равна взятой с соответствующим знаком длине дуги траектории, отделяющей в данный момент времени точку 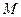 от начала отсчета
от начала отсчета 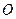 (Рис.1.6). Движение точки будет задано, если задана зависимость дуговой координаты от времени:
(Рис.1.6). Движение точки будет задано, если задана зависимость дуговой координаты от времени: 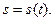 Описанный способ задания движения называется естественным.
Описанный способ задания движения называется естественным.
1.8. Естественный трехгранник
Пусть точка 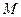 движется по траектории
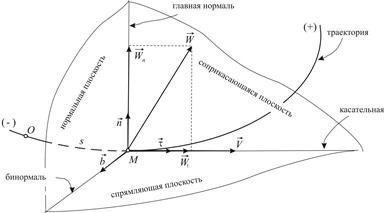
движется по траектории  , на которой установлена криволинейная система отсчета (Рис.1.7).
, на которой установлена криволинейная система отсчета (Рис.1.7).
|
| Рис.1.7 |
В любой точке траектории существует единственная касательная. Обозначим 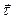 единичный вектор касательной; направлен
единичный вектор касательной; направлен 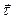 в сторону возрастания дуговой координаты. Нормаль, лежащая в соприкасающейся плоскости, называется главной нормалью. Обозначим
в сторону возрастания дуговой координаты. Нормаль, лежащая в соприкасающейся плоскости, называется главной нормалью. Обозначим  единичный вектор главной нормали;
единичный вектор главной нормали;  направлен в сторону вогнутости траектории. Нормаль, перпендикулярная соприкасающейся плоскости, называется бинормалью. Её единичный вектор
направлен в сторону вогнутости траектории. Нормаль, перпендикулярная соприкасающейся плоскости, называется бинормалью. Её единичный вектор 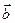 направлен так, чтобы векторы
направлен так, чтобы векторы  и
и 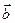 образовывали правую тройку.
образовывали правую тройку.
Соприкасающаяся, нормальная и спрямляющая плоскости образуют естественный трехгранник. Касательная, главная нормаль и бинормаль – оси естественного трехгранника; 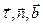 – орты этих осей.
– орты этих осей.
Оси естественного трехгранника играют существенную роль в описании движения точки, поскольку в этих осях вектор скорости и вектор ускорения вычисляются, как будет показано ниже, наиболее удобным образом. Пока отметим только, что разложение этих векторов по осям естественного трехгранника имеет вид:
 (1.8)
(1.8)
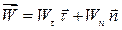 (1.9)
(1.9)
где
 – проекция вектора скорости на направление касательной к траектории;
– проекция вектора скорости на направление касательной к траектории;
 – проекция вектора ускорения на направление касательной к траектории, которая называется касательным ускорением точки;
– проекция вектора ускорения на направление касательной к траектории, которая называется касательным ускорением точки;
 – проекция вектора ускорения точки на направление главной нормали к траектории точки, которая называется нормальным ускорением точки.
– проекция вектора ускорения точки на направление главной нормали к траектории точки, которая называется нормальным ускорением точки.
Оставляя доказательство для самостоятельного изучения, приведём окончательные результаты.
Для вектора скорости получаем:
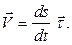 (1.10)
(1.10)
Таким образом,
проекция вектора скорости на направление касательной к траектории точки равна первой производной по времени от дуговой координаты:
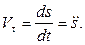 (1.12)
(1.12)
Для вектора ускорения получаем:
 (1.13)
(1.13)
Следовательно, касательное и нормальное ускорения точки определяются по формулам:
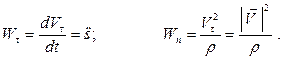 (1.14)
(1.14)
Здесь 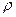 – радиус кривизны траектории в данной точке.
– радиус кривизны траектории в данной точке.
Ускорение точки характеризует изменение вектора скорости. В общем случае вектор скорости может изменять свой модуль и свое направление.
Рассмотрим движение, при котором вектор скорости может изменять свое направление (траектория точки – любая кривая), но модуль скорости остается при этом постоянным. Такое движение называется равномерным. Как видно из формул (1.14) касательное ускорение в этом случае равно нулю. При неравномерном движении касательное ускорение обращается в нуль только в те моменты времени, когда модуль скорости достигает экстремальных значений. Таким образом, касательное ускорение характеризует изменение модуля скорости точки.
Вычисление скорости точки при естественном способе задания ее движения
(Изучить самостоятельно)
Пусть движение точки задано естественным способом. За промежуток времени 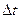 точка переместится по траектории из положения
точка переместится по траектории из положения 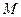 в положение
в положение 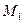 .
.
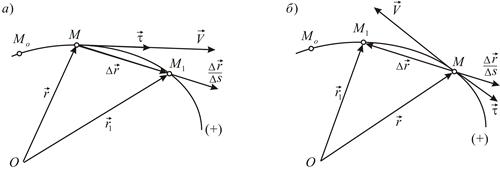
Используя определение вектора скорости, получаем:

Предел отношения длины дуги к длине стягивающей ее хорды по модулю равен единице. Если точка движется в положительном направлении, 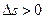 и вектор
и вектор  совпадает по направлению с вектором
совпадает по направлению с вектором 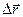 . Если точка движется в отрицательном направлении отсчета,
. Если точка движется в отрицательном направлении отсчета, 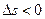 и вектор
и вектор  противоположен по направлению вектору
противоположен по направлению вектору 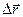 . В обоих случаях предельное направление вектора
. В обоих случаях предельное направление вектора  совпадает с направлением единичного вектора касательной
совпадает с направлением единичного вектора касательной 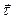 . Таким образом,
. Таким образом, 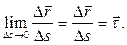
Принимая во внимание, что 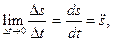 получаем:
получаем:
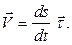
Вычисление ускорения точки при естественном способе задания ее движения
(Изучить самостоятельно)
Используя определение вектора ускорения (1.6) и формулу (2.1), получаем:
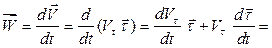
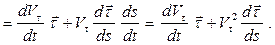 (а)
(а)
Вычислим вектор 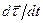 . Прежде всего, найдем направление этого вектора. Рассмотрим тождество
. Прежде всего, найдем направление этого вектора. Рассмотрим тождество
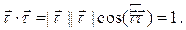
Дифференцируя это тождество по скалярному аргументу  , получаем:
, получаем:
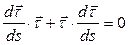 или
или 
Но  в общем случае вектор
в общем случае вектор 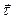 изменяет со временем свое направление, так что
изменяет со временем свое направление, так что  Следовательно, скалярное произведение обратилось в нуль потому, что сомножители взаимно перпендикулярны.
Следовательно, скалярное произведение обратилось в нуль потому, что сомножители взаимно перпендикулярны.
Таким образом, вектор 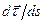 перпендикулярен касательной, т.е. направлен по нормали к траектории. Ранее было показано, что вектор ускорения лежит в соприкасающейся плоскости. Следовательно, речь идет о главной нормали. Таким образом,
перпендикулярен касательной, т.е. направлен по нормали к траектории. Ранее было показано, что вектор ускорения лежит в соприкасающейся плоскости. Следовательно, речь идет о главной нормали. Таким образом,
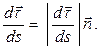 (б)
(б)
Остается вычислить
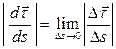
 Пусть
Пусть 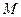 и
и 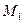 две близкие точки траектории. В точке
две близкие точки траектории. В точке 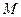 проведем главную нормаль
проведем главную нормаль  В точке
В точке 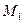 построим нормаль
построим нормаль 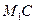 , пересекающую в точке
, пересекающую в точке  главную нормаль, построенную в точке
главную нормаль, построенную в точке 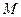 (если траектория плоская кривая, то
(если траектория плоская кривая, то 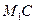 также будет главной нормалью). Угол между двумя близкими касательными, угол
также будет главной нормалью). Угол между двумя близкими касательными, угол  , называется углом смежности. В силу близости точек
, называется углом смежности. В силу близости точек 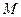 и
и 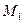 угол между нормалями
угол между нормалями 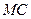 и
и 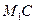 приближенно равен углу
приближенно равен углу  (для плоской кривой это равенство точное). В силу малости дугу
(для плоской кривой это равенство точное). В силу малости дугу  можно считать дугой окружности радиуса
можно считать дугой окружности радиуса  . Тогда
. Тогда  Из равнобедренного треугольника
Из равнобедренного треугольника 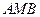 определяем
определяем

Тогда
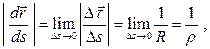
где 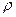 — предельное значение радиуса окружности, дуга которой в бесконечно малой окрестности точки
— предельное значение радиуса окружности, дуга которой в бесконечно малой окрестности точки 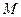 совпадает с дугой траектории. Эта окружность расположена в соприкасающейся плоскости, построенной для точки
совпадает с дугой траектории. Эта окружность расположена в соприкасающейся плоскости, построенной для точки 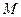 . Ее центр лежит на главной нормали и называется центром кривизны траектории в точке
. Ее центр лежит на главной нормали и называется центром кривизны траектории в точке 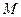 . Ее радиус
. Ее радиус 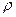 называется радиусом кривизны траектории в точке
называется радиусом кривизны траектории в точке 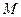 .
.
Окончательно получаем:

Основные определения и аксиомы статики
Совокупность приложенных к телу сил называется системой сил.
Определение 1
Две системы сил называются эквивалентными, если приложение каждой из них к одному и тому же покоящемуся свободному твёрдому телу приводят к одному и тому же движению
Определение 2
Система сил, под действием которой свободное твердое тело может оставаться в покое по отношению к инерциальной системе отсчета, называется уравновешенной или эквивалентной нулю
Определение 3
Если система сил эквивалентна одной силе, то эта сила называется равнодействующей системы сил
В основе действий над силами лежит система простейших правил, которые обычно называют аксиомами статики.
Аксиома 1
Две силы, приложенные в одной точке тела, эквивалентны одной силе (имеют равнодействующую), приложенной в той же точке и равной геометрической сумме этих сил(Рис.3.1)
По существу, приведенное здесь утверждение содержится в сформулированном ранее принципе независимости действия сил.

|
| |
| Рис.2.1 | Рис.2.2 |
Аксиома 2
Не изменяя действия системы сил на тело, к ней можно добавлять или от нее отбрасывать уравновешенную систему сил
Аксиома 3
Сформулированные аксиомы позволяют рассматривать систему сил, приложенную к… Рис.2.3Момент силы относительно точки
Моментом силы относительно точки называется вектор, равный векторному…Момент силы относительно оси
Моментом силы относительно оси называется проекция на ось момента силы, вычисленного относительно любой точки этой оси: Рассмотрим силу , произвольным образом расположенную по отношению к оси . Проведем через точку приложения силы…Пара сил
Парой сил называется система двух сил, равных по модулю и действующих по параллельным прямым в противоположные стороны. Плоскость, в которой расположены силы пары, называется плоскостью действия пары сил. Кратчайшее расстояние между…Классификация сил
При изучении движения или равновесия какого–либо материального объекта (механической системы) его мысленно выделяют из системы окружающих тел. При этом механическое взаимодействие выделенного материального объекта с окружающей средой учитывают, вводя в рассмотрение силы, являющиеся мерой этого механического взаимодействия.
Силы, действующие на механическую систему, разделяют на внешние и внутренние.
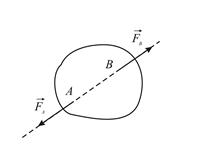
Внутренними 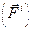 называют силы взаимодействия между точками данной механической системы. Внешними
называют силы взаимодействия между точками данной механической системы. Внешними  называют силы, с которыми на точки данной механической системы действуют окружающие тела, не входящие в систему.
называют силы, с которыми на точки данной механической системы действуют окружающие тела, не входящие в систему.
Часть внешних сил обычно заранее известна — задана. Эти силы называются активными. Как правило, не указывается, со стороны какого тела приложена та или иная активная сила, дан лишь результат взаимодействия механической системы с этим телом — сила.
Другую часть внешних сил составляют реакции связей. Это силы, с которыми на механическую систему действуют тела, находящиеся с ней в непосредственном контакте. Такие тела называются связями. Связи ограничивают перемещения точек механической системы. Под действием активных сил механическая система стремится совершить перемещение, ограниченное связью. При этом она действует на связь с некоторой силой. В соответствии с третьим законом Ньютона связь, в свою очередь, действует на механическую систему с силой реакции. Реакции связей заранее неизвестны, они зависят от вида связи и от приложенных активных сил. Для определения реакций связей необходимо решить соответствующую задачу механики.
ЛЕКЦИЯ 3
Дифференциальные уравнения движения механической системы
(3.1) гдеОсновные свойства внутренних сил
Рассмотрим две любые точки механической системы и . В соответствии с третьим законом Ньютона они взаимодействуют с силами, равными по модулю и… Рис.3.1 илиТеорема об изменении количества движения механической системы
Производная по времени от количества движения механической системы равна геометрической сумме всех приложенных к системе внешних сил.
Теорема об изменении кинетического момента
и сложим все полученные уравнения:Производная по времени от кинетического момента механической системы относительно произвольно выбранного центра равна сумме моментов всех приложенных к системе внешних сил относительно того же центра.
ЛЕКЦИЯ 4
Условия равновесия
Под равновесием в механике традиционно понимают состояние покоя тела по отношению к выбранной системе отсчета. Равновесие по отношению к… Если механическая система покоится по отношению к выбранной системе отсчета,…Для равновесия механической системы необходимо, чтобы сумма проекций всех приложенных к системе внешних сил на каждую из трех взаимно перпендикулярных осей равнялась нулю и сумма моментов всех внешних сил относительно этих осей равнялась нулю.
Вообще говоря, условия (3.10) являются также и достаточными условиями равновесия абсолютно твердого тела, но доказательство этого утверждения выходит за рамки рассматриваемого здесь курса. Для геометрически изменяемой механической системы эти условия будут только необходимыми.
Равновесие системы сил, линии действия которых лежат в одной плоскости
(3.11) Рис.3.2 где – произвольно выбранная точка плоскости . При этом для вычисления момента силы относительно оси применимо простое…Расчет ферм
Особое место в ряду статических задач занимает расчет ферм. Фермой называется жесткая конструкция из прямолинейных стержней (Рис.3.3). Если все… Рис.3.3 В результате полного расчета фермы необходимо определить реакции опор и усилия во всех стержнях фермы.Равновесие тела при наличии трения
Как известно, при скольжении тела по опорной поверхности возникает сопротивление, тормозящее скольжение. Это явление учитывается путем введения в… Рис.3.4Сила трения действует в общей касательной плоскости к поверхностям соприкасающихся тел и противоположна тому направлению, в котором активно действующие силы стремятся сдвинуть тело.
2. Модуль силы трения при покое принимает всякий раз значение, необходимое для предотвращения проскальзывания тела по поверхности, но не может превзойти некоторого предельного значения, которое достигается на грани перехода тела от состояния покоя к состоянию скольжения:
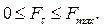
3. Максимальное значение силы трения при покое пропорционально модулю силы нормальной реакции поверхности:
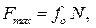
где  — коэффициент трения при покое, который определяется экспериментально. Коэффициент
— коэффициент трения при покое, который определяется экспериментально. Коэффициент  зависит от материала тел, шероховатости, влажности, температуры трущихся поверхностей, но на его значение в широких пределах не влияют размеры площадки контакта тел.
зависит от материала тел, шероховатости, влажности, температуры трущихся поверхностей, но на его значение в широких пределах не влияют размеры площадки контакта тел.
4. При скольжении тела по шероховатой поверхности сила трения пропорциональна силе нормальной реакции поверхности:
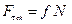
и направлена в сторону, противоположную скольжению. Динамический коэффициент трения 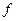 (коэффициент трения скольжения), помимо прочего, может зависеть от относительной скорости скольжения.
(коэффициент трения скольжения), помимо прочего, может зависеть от относительной скорости скольжения.
Центр параллельных сил
Центром параллельных сил называется точка, вокруг которой поворачивается…Центр тяжести тела
Центр масс механической системы. Теорема о движении центра масс
Центром масс механической системы называется точка , радиус–вектор которой… (4.8)ЛЕКЦИЯ 5
Одной из важнейших задач механики является описание движения абсолютно… Следующая проблема состоит в том, чтобы, зная законы движения тела, определить скорость и ускорение любой точки…Поступательное движение твердого тела
Рассмотрим две любые точки и тела. В любой момент времени имеет место… (5.1)Вращение твердого тела вокруг неподвижной оси
Кинематика вращательного движения твердого тела
Рис.5.2 остаются неподвижными. Эта прямая называется осью вращения. Чтобы получить… Проведем в теле сечение, перпендикулярное оси вращения. Через любую точку сечения проведем перпендикуляр к сечению .…Скоростью тела.
(5.4) Формула (5.4) называется формулой Эйлера. На Рис.5.5 представлено распределение скоростей точек сечения тела,…Дифференциальное уравнение вращательного движения твердого тела
(5.6)Плоскопараллельное движение твердого тела
Кинематика плоскопараллельного движения твердого тела
Проведем сечение тела параллельное основной плоскости (Рис.5.8). Через любую точку сечения проведем отрезок , перпендикулярный основной плоскости.… Таким образом, движение сечения полностью определяет плоскопараллельное… Рис. 5.8 …Дифференциальные уравнения плоскопараллельного движения твердого тела
Такой выбор связан, прежде всего, с тем, что теорема о движении центра масс позволяет получить дифференциальные уравнения, служащие для определения… (5.11)Система Кенига. Первая теорема Кенига
Пусть система отсчета неподвижная (инерциальная). Система движется поступательно по отношению к , причем ее начало во все время движения совпадает… Установим связь между кинетическими моментами механической системы…Теорема об изменении кинетического момента относительно центра масс механической системы
(Изучить самостоятельно)
Подставим последний результат в теорему об изменении кинетического момента относительно неподвижного центра 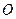 :
:

или

Второе слагаемое в левой части равенства равно нулю, как скалярное произведение коллинеарных сомножителей. Используя теорему о движении центра масс, получаем:
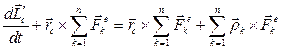
или
 .
.
Таким образом,
Производная по времени от кинетического момента механической системы относительно ее центра масс равна сумме моментов относительно центра масс всех приложенных к системе внешних сил.
ЛЕКЦИЯ 6
Кинетическая энергия механической системы
Работа и мощность силы. Потенциальная энергия
Половина произведения массы точки на квадрат ее скорости называется… (6.1)Теорема об изменении кинетической энергии механической системы
Теорема об изменении кинетической энергии относится к числу общих теорем динамики наряду с доказанными ранее теоремами об изменении количества… Умножим каждое из дифференциальных уравнений движения точек механической… илиРабота внутренних сил геометрически неизменяемой механической системы
Особый случай представляет геометрически неизменяемая механическая система, в частности, абсолютно твердое тело. Скорости двух любых точек и геометрически неизменяемой механической системы…Вычисление кинетической энергии абсолютно твердого тела
1. При поступательном движении в любой момент времени скорости всех точек тела одинаковые. Полагая в формуле (6.1) получаем: (6.10)Работа внешних сил, приложенных к абсолютно твердому телу
гдеНекоторые частные случаи вычисления работы силы
Работа силы тяжести
При вычислении работы силы тяжести будем считать, что мы рассматриваем ограниченную область пространства вблизи поверхности Земли, размеры которой… Направим ось вертикально вверх. Точка с массой перемещается по некоторой… Вычислим работу силы тяжести. Используя формулу (6.3), получаем:Работа упругой силы
Понятие упругой силы обычно ассоциируется с реакцией линейно–упругой пружины. Направим ось вдоль пружины в сторону ее растяжения. Под понимаем… Сила реакции пружины пропорциональна ее удлинению где – коэффициент жесткости… Вычислим мощность упругой силы:Работа вращающего момента
Пусть сила приложена в некоторой точке тела, имеющего ось вращения. Тело вращается с угловой скоростью . Вычислим мощность и работу силы. Точка…ЛЕКЦИЯ 7
Классификация связей
Основная идея, положенная в основу подхода к решению задач в аналитической механике, состоит в том, чтобы разделить задачу определения закона движения механической системы и задачу определения неизвестных реакций связей. Для этого необходимо получить дифференциальные уравнения движения механической системы в виде, не содержащем реакций связей. Напомним основные положения, касающиеся связей, наложенных на механическую систему, и рассмотрим их классификацию.
Механическая система называется свободной, если ее точки могут занимать любые положения в пространстве, а их скорости могут принимать любые значения. В противном случае система называется несвободной. Очевидно, для несвободной системы должны быть заданы ограничения, налагаемые на координаты и скорости точек системы. Эти ограничения называют связями. Они могут быть записаны в виде уравнений или неравенств, связывающих время, координаты и скорости точек системы. Конструктивно связи реализуются в виде шарниров, поверхностей, стержней, нитей и т.п.
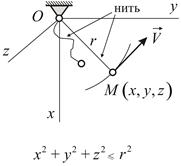
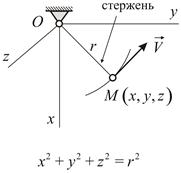
Если механическая система может покинуть связь, то такая связь называется неудерживающей; в противном случае – удерживающей. На Рис.7.1 изображен шарик, привязанный к концу нерастяжимой нити, Такой шарик при натянутой нити движется по сфере радиуса 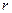 , но может уйти и внутрь этой сферы. При этом нить не натянута (как– бы отсутствует). Это пример неудерживающей связи в отличие от случая, изображенного на Рис.7.2, где такой же шарик находится на конце нерастяжимого стержня. Удерживающие связи записываются в виде уравнений, а неудерживающие – в виде неравенств, связывающих координаты точек системы.
, но может уйти и внутрь этой сферы. При этом нить не натянута (как– бы отсутствует). Это пример неудерживающей связи в отличие от случая, изображенного на Рис.7.2, где такой же шарик находится на конце нерастяжимого стержня. Удерживающие связи записываются в виде уравнений, а неудерживающие – в виде неравенств, связывающих координаты точек системы.
| 
| 
| ||
| Рис. 14.1 | Рис. 14.2 | Рис. 14.3 |
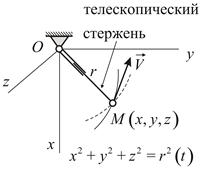
Рассмотренные в этих двух примерах связи являются стационарными, в отличие от случая, изображенного на Рис.7.3, где в качестве опоры используется телескопический стержень, длина которого может изменяться со временем. Итак, если вид связи не изменяется со временем, связь называется стационарной; в противном случае – нестационарной. В уравнения (неравенства) стационарных связей время не входит явным образом.
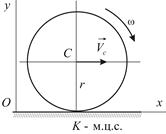
Связи могут налагать ограничения не только на координаты точек, но и на их скорости. Например, при качении без скольжения колеса по неподвижной поверхности (Рис.7.4) ограничения, налагаемые связью (поверхность) могут быть выражены уравнениями:  Хотя второе из этих уравнений носит относительно координат дифференциальный характер, оно может быть проинтегрировано
Хотя второе из этих уравнений носит относительно координат дифференциальный характер, оно может быть проинтегрировано
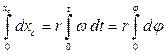
и заменено алгебраическим соотношением 
| 
| |
| Рис. 7.4 | Рис. 7.5 |
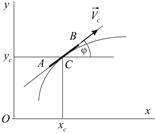
Рассмотрим другой пример. Конек  скользит по ледяной поверхности, принятой за координатную плоскость
скользит по ледяной поверхности, принятой за координатную плоскость  (Рис.7.5). Конек имеет выпуклое лезвие, которое касается льда только в одной точке
(Рис.7.5). Конек имеет выпуклое лезвие, которое касается льда только в одной точке  . Положение конька задается двумя координатами точки
. Положение конька задается двумя координатами точки  и углом
и углом  . Конек затачивается таким образом, чтобы отсутствовало поперечное скольжение в направлении, перпендикулярном
. Конек затачивается таким образом, чтобы отсутствовало поперечное скольжение в направлении, перпендикулярном  . Иначе говоря, скорость точки касания
. Иначе говоря, скорость точки касания  должна быть направлена вдоль конька, т.е.
должна быть направлена вдоль конька, т.е.
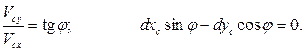
Это уравнение связи (в отличие от предыдущего примера) нельзя проинтегрировать, не зная законов движения конька 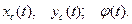
Связи называются голономными, если их уравнения могут быть записаны в виде, не содержащем производных от координат по времени или дифференциалов координат.
Связи называются неголономными, если их уравнения содержат неинтегрируемым образом производные от координат по времени или дифференциалы координат.
В дальнейшем будем рассматривать только голономные удерживающие стационарные 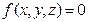 и нестационарные
и нестационарные 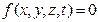 связи. Изучение неголономных систем представляет значительные трудности и не входит в число вопросов, излагаемых в данном курсе. Если же на систему наложены неудерживающие связи, то решение задачи можно разбить на ряд временных интервалов, на одних из которых связь действует как удерживающая (на Рис.7.1 нить натянута), а на других как бы отсутствует (нить не натянута).
связи. Изучение неголономных систем представляет значительные трудности и не входит в число вопросов, излагаемых в данном курсе. Если же на систему наложены неудерживающие связи, то решение задачи можно разбить на ряд временных интервалов, на одних из которых связь действует как удерживающая (на Рис.7.1 нить натянута), а на других как бы отсутствует (нить не натянута).
Возможные скорости и возможные перемещения
Возможной скоростью материальной точки называется любая скорость, которую может иметь несвободная материальная точка, не нарушая наложенных на нее в… Заметим, что возможная скорость не реализуется как следствие действия приложенных к точке сил. Это – мыслимый набор…Идеальные связи
(7.1) Учитывая важность понятия идеальной связи, рассмотрим часто встречающиеся… 1.Пусть опорой для тела служит некоторая поверхность, по которой тело может скользить (Рис.7.8). В общем случае…ЛЕКЦИЯ 8
Принцип возможных перемещений
Рассмотрим механическую систему, состоящую из материальных точек. Для ее равновесия необходимо и достаточно, чтобы суммы всех сил, действующих на… (8.1)Для равновесия механической системы с идеальными, удерживающими, стационарными связями необходимо и достаточно, чтобы сумма мощностей всех приложенных к системе активных сил при любых возможных скоростях ее точек равнялась нулю и скорости всех точек в начальный момент времени равнялись нулю.
Пример 1
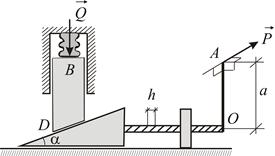
Определить зависимость между модулями сил 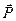 и
и  в клиновом прессе, если сила приложена к концу рукоятки длины
в клиновом прессе, если сила приложена к концу рукоятки длины  перпендикулярно плоскости, содержащей рукоятку и ось винта (Рис.8.1). Шаг винта равен
перпендикулярно плоскости, содержащей рукоятку и ось винта (Рис.8.1). Шаг винта равен  . Угол при вершине клина
. Угол при вершине клина  .
.
Дадим системе возможное перемещение: пусть  – угол поворота рукоятки;
– угол поворота рукоятки; 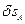 – перемещение точки
– перемещение точки 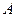 ;
;  – горизонтальное перемещение клина;
– горизонтальное перемещение клина; 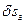 – вертикальное перемещение точки
– вертикальное перемещение точки 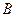 .
.
|
| Рис.8.1 |
При исследовании условий равновесия механизмов в зависимости от конкретной задачи, исходя из соображений удобства, можно использовать как возможные скорости, так и возможные перемещения. Для сравнения в этом первом разбираемом примере рассмотрим и возможные перемещения, и возможные скорости.
Условия равновесия системы можно записать в виде (8.2): 
Возможные перемещения связаны между собой соотношениями
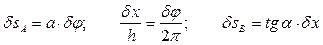 . Отсюда:
. Отсюда: 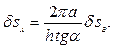
Теперь условия равновесия записываются в виде: 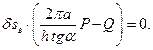
Отсюда: 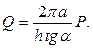
Пример 2
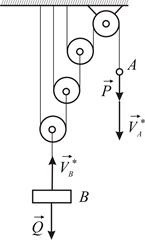
Полиспаст состоит из неподвижного блока и  подвижных блоков (Рис.8.2). Определить в случае равновесия отношение веса
подвижных блоков (Рис.8.2). Определить в случае равновесия отношение веса 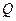 поднимаемого груза
поднимаемого груза 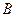 к величине силы
к величине силы 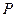 , приложенной к свободному концу
, приложенной к свободному концу 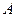 троса.
троса.
|
| Рис.8.2 |
Условие равновесия (8.5) имеет вид 
Рассмотрим первый из подвижных блоков. Точка 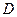 – мгновенный центр скоростей блока. Возможная скорость точки
– мгновенный центр скоростей блока. Возможная скорость точки  численно равна возможной скорости точки
численно равна возможной скорости точки 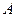 . Следовательно,
. Следовательно, 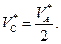 Скорость центра каждого последующего подвижного блока равна половине скорости центра предыдущего подвижного блока. Таким образом,
Скорость центра каждого последующего подвижного блока равна половине скорости центра предыдущего подвижного блока. Таким образом, 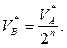
Подставляя полученный результат в условие равновесия, имеем:

Общее уравнение динамики
Рассмотрим механическую систему, состоящую из материальных точек, на которую наложены идеальные удерживающие связи. Уравнения движения точек имеют…В каждый момент времени для механической системы с идеальными удерживающими связями сумма работ всех активных сил и всех сил инерции на любом возможном перемещении системы равна нулю.
Пример
Призма массы  может скользить по идеально гладкой горизонтальной поверхности. В вершине призмы закреплена ось барабана лебедки. Конец троса прикреплен к оси катка, который катится без скольжения по боковой поверхности призмы. Барабан лебедки и каток — сплошные однородные цилиндры одинаковой массы
может скользить по идеально гладкой горизонтальной поверхности. В вершине призмы закреплена ось барабана лебедки. Конец троса прикреплен к оси катка, который катится без скольжения по боковой поверхности призмы. Барабан лебедки и каток — сплошные однородные цилиндры одинаковой массы 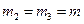 и одинакового радиуса
и одинакового радиуса 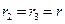 . К барабану лебедки приложен постоянный вращающий момент
. К барабану лебедки приложен постоянный вращающий момент 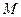 . Составить дифференциальные уравнения движения системы.
. Составить дифференциальные уравнения движения системы.

|
| Рис.8.3 |
Силовая и кинематическая схемы представлены на Рис.8.3. Общее уравнение динамики в рассматриваемом случае имеет вид:

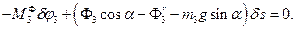
Система имеет две степени свободы. В качестве независимых координат примем координату призмы  и относительную координату оси катка
и относительную координату оси катка  . Кинематические условия, налагаемые связями, имеют вид:
. Кинематические условия, налагаемые связями, имеют вид: 
Отсюда:  и
и 
Учитывая, что



получаем общее уравнение динамики в виде:
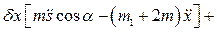

Поскольку возможные перемещения  и
и 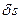 могут принимать любые значения и не зависят друг от друга, общее уравнение динамики распадается на систему двух дифференциальных уравнений относительно координат
могут принимать любые значения и не зависят друг от друга, общее уравнение динамики распадается на систему двух дифференциальных уравнений относительно координат  и
и  :
:

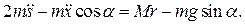
– Конец работы –
Используемые теги: Теоретическая, Механика, Краткий, курс, Конспект, лекций, ПО, теоретической, механике0.118
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: ТЕОРЕТИЧЕСКАЯ МЕХАНИКА- краткий курс КОНСПЕКТ ЛЕКЦИЙ ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов