Представление пространственных форм.

 

Пусть надо изобразить пространственную кривую:

 

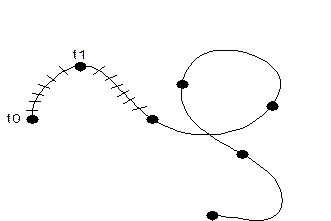
Всю кривую разобьём на криволинейные отрезки. В пределах кусочка {t0-t1}

зададим некоторый параметр t. t изменяется в диапазоне от 0 до 1.

Пространственные координаты этих кусочков:

(*)

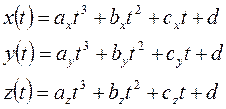Но чтобы обеспечить хорошую стыковку этих кусочков нужно соблюдать сле-

дующие условия:

1) При стыковке по уровню - непрерывность по координатам;

2) При стыковке по уровню - непрерывность по первой производной;

3) При стыковке по уровню 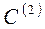- непрерывность на уровне второй произ-

Водной.

 

Математическое вычисление коэффициентов полиномов (*):

 

1) В форме Эрмитта:

Для куска кривой должны быть известны:

а) координаты начальной и конечной точек:

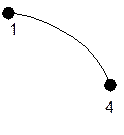
Координаты:

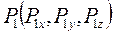и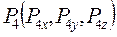

 

Рассмотрим вычисления только относительно X:

;

 

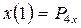
б) производные (по каждой из координат) в начальной и конечной точках:

;

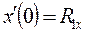Для нахождения коэффициентов полиномов (*) обозначим:

 

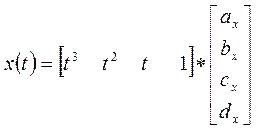
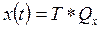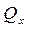, где - матрица коэффициентов

Пусть :

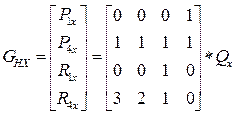
- геометрический вектор Эрмитта (т.е. наши начальные донные).

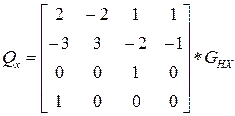
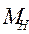, где - матрица Эрмитта.

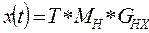
Анологичные вычисления производятся для Y и Z.

Таким образом мы получаем следующие формулы:

и

 

 

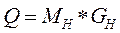
Кривая построенная по этим данным:

V1 и V2 – вектора скорости

 

Касательная к кривой задаётся от-

ношением:

 

 

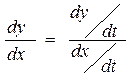
Если мы хотим соединить несколько кусочков, то в месте стыковки направле-

ние касательных для конца 1-го и начала 2-го отрезков должно совпадать.

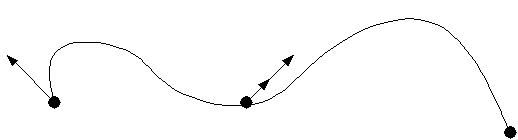
Скорости могут отличаться по длине, но они должны лежать на одной касатель-

ной.

 

2) Задание коэффициентов в форме Безье:

В этом случае точки 2 и 3 являются управляющими(управляют формой кривой),

а точки 1 и 4 являются опорными точками (кривая проходит через них).

Представление по Эрмиту:

;

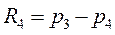
А Безье предложил следующее:

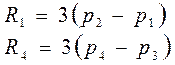
Т.е. кривая должна выити из точки 1 и прийти в точку 4, а лежать она будет вну-

три четырёхугольника, образованного точками 1, 2, 3, 4.

 

 

По Эрмиту:

, где под p может подразумеваться либо x, либо y, либо z

Запишем эту формулу для Безье:

;

 

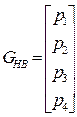Откуда следует, что:

,

где - матрица Безье.

 

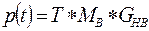, где - матрица коэффициентов.

 

Когда мы имеем несколько кусочков кривой описанных Безье, то для стыков-

ки надо соблюсти следующее условие:

т.е точки 3 и 5 должны лежать на одной прямой (для данного случая). Это

обеспечивает одинаковую касательную в точке стыковки.

 

3) Форма сплайна:

Идея: хотим провести гладкую прямую через набор точек.

Пример 1:

 

 

1) Берём первые 4-ре точки и по ним считаем уравнение кусочка кривой, но

это уравнение опишет нам кусочек кривой между точками 2 и 3.

2) Берём следующие 4-ре точки и получаем кусочек кривой между точками 3

и 4, причём можно подобрать такие коэффициенты , что в точке 3 стыков-

ка будет гладкостью .

Тогда:

;

 

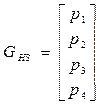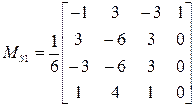
Примечание:

В рассмотренном выше примере все точки являются управляющими, т.е. кривая

проходит вблизи точек, а не по ним.

Обеспечивается гладкость .

Относительно решения проблемы кусочка кривой между точками 1 и 2 можно

предложить следующие варианты:

1) можно добавить фиктивные точки;

2) сделать замкнутую кривую;

3) “слить” две точки в одну.

 

Пример 2:

Нам нужно чтобы кривая прошла через какие-то фиксированные точки:

 

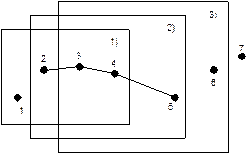Процесс обработки тот же, что и в примере 1.

Отличие в том, что в данном случае все точки опорные и кривая проходит не

вблизи , а точно по точкам. Следовательно мы проигрываем в гладкости, обе-

спечивая только уровень .

 

Для данного случая:

;