Частные случаи линейных преобразований
1.) Разделимые линейные преобразования
A(n1, n2, m1, m2) = Ac(n1, m1) ∙ As(n2, m2)
B(n1, n2, m1, m2) = Bc(n1, m1) ∙ Bs(n2, m2)
F = Ac ∙ F ∙ AsT

F = Bc ∙  ∙ BsT ; Bc = Ac-1; Bs = As-1.
∙ BsT ; Bc = Ac-1; Bs = As-1.
2.) Свёртка
 VR(x, y) =
VR(x, y) = 
 VS(i, j) ∙ Q’(x-i, y-j)
VS(i, j) ∙ Q’(x-i, y-j)
|
|

|

 Vs Fs
Vs Fs
|
|
|
 | |||||
 | |||||
| |||||
|
|
|
 Q’ FQ
Q’ FQ
VR(r1, r2) = 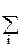
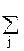 VS(i, j) ∙ Q’(r1-i, r2-j) (1)
VS(i, j) ∙ Q’(r1-i, r2-j) (1)
Fs(m1, m2) = 
 VS(n1, n2) ∙ A(n1, n2, m1, m2) (2)
VS(n1, n2) ∙ A(n1, n2, m1, m2) (2)
FQ(q1, q2) = 
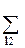 Q’(l1, l2) ∙ A(l1, l2, q1, q2) (3)
Q’(l1, l2) ∙ A(l1, l2, q1, q2) (3)
VR(r1, r2) = 
 FR(p1, p2) ∙ B(p1, p2 , r1, r2) (4)
FR(p1, p2) ∙ B(p1, p2 , r1, r2) (4)
FR(i ,j) = FS(i ,j) ∙ FQ(i ,j) (5)
i , j = 0……………N-1.
Подставим величины из формул (2), (3), (5) в формулу (4).
В результата этого мы получим :
VR(r1, r2) = 
 (
(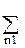
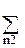 VS(n1, n2) ∙ A(n1, n2, p1, p2) ∙
VS(n1, n2) ∙ A(n1, n2, p1, p2) ∙
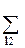 Q’(l1, l2) ∙
Q’(l1, l2) ∙
A(l1, l2, p1, p2)) ∙ B(p1, p2 , r1, r2) = 


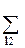 VS(n1, n2) ∙ Q’(l1, l2) ∙
VS(n1, n2) ∙ Q’(l1, l2) ∙ 
 A(n1, n2, p1, p2) ∙ A(l1, l2, p1, p2) ∙ B(p1, p2 , r1, r2)
A(n1, n2, p1, p2) ∙ A(l1, l2, p1, p2) ∙ B(p1, p2 , r1, r2)
Выделенная в формуле подчёркиванием часть зависит только от ядер.
 Она равна 1 при n1= r1 – l1 или n2= r2 – l2
Она равна 1 при n1= r1 – l1 или n2= r2 – l2
 |
 0 , иначе
0 , иначе
d(n1+l1– r1) ∙ d(n2+l2– r2) (дельта – функция.)
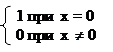 |
d(x)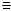
A(n1, n2, p1, p2) = AS(n1, p1) ∙ AC(n2, p2)
|
 AS = AC = A
AS = AC = A
BS = BC = B
B(p1, p2, r1, r2) = BS(p1, r1) ∙ BC(p2, r2)
|

 A(n1, n2, p1, p2) ∙ A(l1, l2, p1, p2) ∙ B(p1, p2 , r1, r2) = d(n1+l1– r1) ∙ d(n2+l2– r2)
A(n1, n2, p1, p2) ∙ A(l1, l2, p1, p2) ∙ B(p1, p2 , r1, r2) = d(n1+l1– r1) ∙ d(n2+l2– r2)
 |
d(x)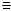
A(n1, n2, p1, p2) = AS(n1, p1) ∙ AC(n2, p2) (1)
AS = AC 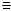 A’
A’
B(p1, p2, r1, r2) = B’(p1, r1) ∙ B’(p2, r2) (2)
Воспользовавшись формулами (1) и (2) преобразуем выражение (**) :
 A’(n1, p1) ∙A’(l1, p1) ∙ B’(p1, r1) ∙
A’(n1, p1) ∙A’(l1, p1) ∙ B’(p1, r1) ∙ A’(n2, p2) ∙A’(l2, p2) ∙ B’(p2, r2) =
A’(n2, p2) ∙A’(l2, p2) ∙ B’(p2, r2) =
= d(n1+l1– r1) ∙ d(n2+l2– r2)
A’(n, p) = anp ; A’(l, p) = alp ; B’(p, r) = a-pr
a-pr

 ap(n+l-r) = d (n+l– r)
ap(n+l-r) = d (n+l– r)
n+l– r 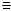 n
n
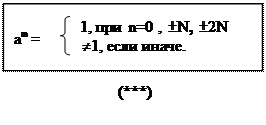 | |||||
 | |||||
 | |||||
Пусть n = 0,  N.
N.
Эквивалентность выражения (*) докажем , домножив обе части уравнения на
(1 - an).

| |
 apn =
apn =  apn -
apn -  an(p+1) = 1+
an(p+1) = 1+ 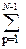 apn -
apn -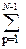 apN – anN =1 – (aN)n = 0
apN – anN =1 – (aN)n = 0
 1 = N∙ d(0) ; аналогично для n=N,-N.
1 = N∙ d(0) ; аналогично для n=N,-N.
Теперь уравнение (***) будет основным
Решим его :
aN =1 = ei∙2p - комплексное преобразование 1.
a = ei∙2p/N – решение в области комплексных чисел.
|
 ) =
) = anm ∙F(n) =
anm ∙F(n) =  ei∙(2p/N) ∙n∙m ∙F(n) =
ei∙(2p/N) ∙n∙m ∙F(n) =
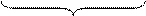
 =
= F(n) ∙cos (
F(n) ∙cos ( ∙n ∙m ) + i ∙
∙n ∙m ) + i ∙  F(n) ∙sin(
F(n) ∙sin( ∙n ∙m ) =
∙n ∙m ) =
|
| ||||
F(n) =  ∙
∙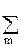 a-nm ∙
a-nm ∙  ) =
) = 
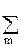 ei∙(2p/N) ∙n∙m ∙
ei∙(2p/N) ∙n∙m ∙  ) =
) = 
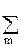
 ) ∙cos (
) ∙cos ( ∙n ∙m ) –
∙n ∙m ) –
- i∙ 
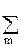
 ) ∙ sin(
) ∙ sin( ∙n ∙m )
∙n ∙m )
Связь между спектральными коэффициентами и корреляционной функцией
Пусть имеется входной сигнал, описываемый функцией F(n). Тогда квадрат коэффициента корреляции k равен:
k2 = 
 F(n) ∙ sin(
F(n) ∙ sin( ∙n ∙m +y) =
∙n ∙m +y) = 
 F(n) ∙ sin(
F(n) ∙ sin( ∙n ∙m) ∙ cos(y) +
∙n ∙m) ∙ cos(y) + 
 F(n) ∙ cos(
F(n) ∙ cos( ∙n ∙m) ∙ sin(y)
∙n ∙m) ∙ sin(y)
Так как 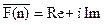
Принимая  , и
, и 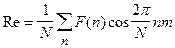 , получим:
, получим:
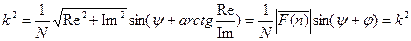
 ;
;  ;
; 
Оценка сложности:
1. Вычисляются спектральные коэффициенты строк
2. Вычисляются спектральные коэффициенты столбцов
Для каждого отсчета надо сделать N операций
 ,
,
где N — сложность вычисления одного коэффициента, k — коэффициент сложности работы с комплексными числами
Сложность прямого преобразования:
 — это только по строкам
— это только по строкам
Аналогично получается сложность по столбцам
Тогда общая сложность:
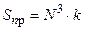 — суммарная сложность прямого преобразования
— суммарная сложность прямого преобразования


SS = Sпр + Sобр = 2N3∙k
k – коэффицент , отражающий специфику работы с комплексными числами.
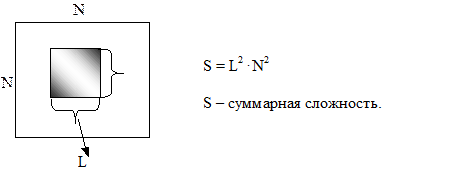
Сравним SS и S :
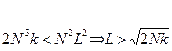
Проверка
Пусть N=512 ; k=2.
Ответ : L > 45. – выгодно использовать пространственное преобразование при больших фильтрах.