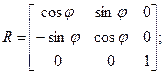Двумерные геометрические преобразования
Параллельный перенос

Параллельный перенос в плоском случае имеет вид:
 |
x` = x + Dx
y` = y + Dy
[x’, y’] = [x, y] + [Dx, Dy]
 |  |  |
P’ P T
или в векторной форме:
| P` = P + T, |
где P` = [x` y`] - вектор-строка преобразованных координат,
где x, y - исходные координаты точки,
Tx, Ty - величина сдвига по осям,
x`, y` - преобразованные координаты.
P = [x y] - вектор-строка исходных координат,
P` = [x` y`] - вектор-строка преобразованных координат,
T = [Tx Ty] - вектор-строка сдвига.
Масштабирование

Преобразование масштабирования относительно начала координат имеет вид:
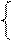 x` = x ·Sx
x` = x ·Sx
y` = y ·Sy или
 |
Sx 0
[x`, y`] = [x, y] ·
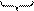
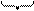 0 Sy
0 Sy
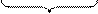 P` P
P` P
S
или в матричной форме:
| P` = P ·S, |
где Sx, Sy - коэффициенты масштабирования по осям, а
S - матрица масштабирования
Поворот
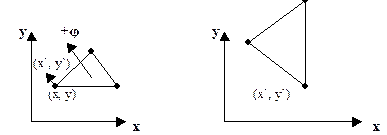
Преобразование поворота относительно начала координат имеет вид:

x`= x·cos(φ) – y·sin(φ)
y`= x·sin(φ) + y·cos(φ)
или
 cos(φ) sin(φ)
cos(φ) sin(φ)
[x`, y`] = [x, y] ·
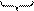
 –sin(φ) cos(φ)
–sin(φ) cos(φ)
 P` P
P` P
R
Где R – матрица поворота
φ – положительный угол поворота
или в матричной форме:
| P` = P ·R, |
Столбцы и строки матрицы поворота представляют собой взаимно ортогональные единичные векторы. В самом деле квадраты длин векторов-строк равны единице:
| cosf·cosf+sinf·sinf = 1 и |
| (-sinf) ·(-sinf)+cosf·cosf = 1, |
а скалярное произведение векторов-строк есть
| cosf·(-sinf) + sinf·cosf = 0. |
Так как скалярное произведение векторов A ·B = |A| ·|B| ·cosy, где |A| - длина вектора A, |B| - длина вектора B, а y - наименьший положительный угол между ними, то из равенства скалярного произведения двух векторов-строк длины 1 следует, что угол между ними равен 90°.
Аналогичное можно показать и для векторов-столбцов. Кроме того вектора-столбцы представляют собой такие единичные векторы, которые после выполнения преобразования, заданного этой матрицей, совпадут с осями. В самом деле, произведение первого столбца на матрицу есть
 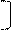 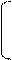   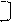
| cosf | -sinf | · | cosf | sinf | = | , | |||||||||||||||
| -sinf | cosf |
т.е. это единичный вектор вдоль оси X. Аналогично, произведение второго столбца на матрицу даст вектор [ 0 1 ]. Это позволяет сформировать матрицу, если известны результаты преобразования.
Преобразование в однородную систему координат
Как видно двумерные преобразования имеют различный вид. Сдвиг реализуется сложением, а масштабирование и поворот - умножением. Это различие затрудняет формирование суммарного преобразования и устраняется использованием двумерных однородных координат точки, имеющих вид:
| [ X Y W ]. |
Здесь W - произвольный множитель не равный 0.
Двумерные декартовые координаты точки получаются из однородных делением на множитель W:
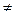 x = X / W, y = Y / W, W 0 x = X / W, y = Y / W, W 0
|
Однородные координаты можно представить как промасштабированные с коэффициентом W значения двумерных координат, расположенные в плоскости с Z = W.
В силу произвольности значения W в однородных координатах не существует единственного представления точки, заданной в декартовых координатах.
Преобразования параллельного переноса, масштабирования и поворота в однородных координатах относительно центра координат все имеют одинаковую форму произведения вектора исходных координат на матрицу преобразования.
Будем брать W=1.
Параллельный перенос:
 |
1 0 0
[X`, Y`, 1]=[X, Y, 1]· 0 1 0
Dx Dy 1

Перемножив, получим: [X + Dx, Y + Dy, 1].
Масштабирование:
P` = P·S; где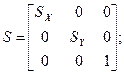
Поворот:
Рё = Р·R; где