Нормы векторов и матриц.

Поскольку численные методы по своей природе являются приближенными (по крайней мере, ввиду наличия вычислительной погрешности, обусловленной приближенностью компьютерной арифметики), важное значение имеют оценки погрешности (разности векторов точного и приближенного решений). Для этих целей используются различные нормы линейного векторного пространства. Напомним, что нормой вектора называется произвольный линейный положительно определенный функционал (скалярная функция векторного аргумента), который для любого элемента векторного пространства удовлетворяет трем условиям, известным как аксиомы нормы:

1. – положительная определенность;

2. , – линейность при умножении на скаляр;

3. 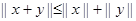– неравенство треугольника.

Векторные нормы, получившие наиболее широкое распространение в численном анализе:

– Евклидова норма (при соответствующем определении скалярного произведения);

– максимальная норма;

– энергетическая норма, порожденная положительно определенным самосопряженным оператором .

Аксиоматику матричной нормы, в отличие от нормы вектора, полезно пополнить дополнительным условием. Поскольку для матриц определена операция умножения, то естественным является требование

– аксиома мультипликативности матричной нормы.

Аксиома мультипликативности матричной нормы тесно связана с требованием согласованности норм матриц и векторов. В частности, для мультипликативной нормы автоматически выполняется оценка 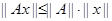(вектор 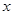в данном случае может трактоваться как матрица, имеющая размерность 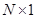). Для получения не улучшаемых оценок произведения матрицы на вектор используют нормы матриц, подчиненные соответствующим векторным нормам.

Определение.Норма матрицы 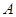, подчиненная векторной норме 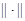определяется числом

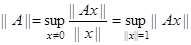(1.1)

В случае квадратных матриц из определения подчиненной матричной нормы следует ее согласованность, мультипликативность и минимальность среди всех возможных согласованных норм. Подчиненные матричные нормы для приведенных выше основных векторных норм вычисляются следующим образом.

– матричная норма, подчиненная векторной Евклидовой норме, равна максимальному сингулярному числу матрицы. Сингулярные числа матрицы вычисляются как корень квадратный из собственных значений матрицы 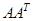. Для симметричной, положительно определенной матрицы сингулярные числа совпадают со спектром собственных значений данной матрицы.

. В качестве данной нормы выступает максимальное значение сумм абсолютных величин элементов строк матрицы.

Выбор конкретной нормы для получения оценок приближенного решения определяется в основном целью исследований и спецификой задачи. При этом следует иметь в виду, что нормы конечномерного линейного векторного пространства эквивалентны с точностью до постоянного множителя. Например, для норм и 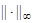имеют место оценки

. (1.2)