Метод Гаусса

Большинство прямых методов решения систем ЛАУ в той или иной мере наследуют идею алгоритма последовательного исключения неизвестных – метода Гаусса. Идея достаточно прозрачна. Если матрица задачи, например, является верхней треугольной, в которой 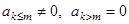, то произвольное уравнение системы имеет вид

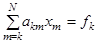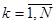, . (2.1)

Последнее уравнение системы содержит всего лишь одно неизвестное 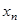,.и его значение вычисляется первым:

. (2.2)

Остальные неизвестные вычисляются последовательно по явным формулам

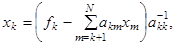
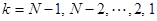. (2.3)

Совершенно аналогичный алгоритм может быть построен и для задачи с нижней треугольной матрицей.

Суть метода Гаусса состоит в приведении матрицы задачи к верхнему (нижнему) треугольному виду. Для этих целей используются тождественные преобразования системы. В частности, решение задачи не меняется при замене произвольной строки системы на линейную комбинацию данной строки и произвольного числа других строк системы. Используя такого рода преобразования, можно последовательно, столбец за столбцом, исключить переменные, находящиеся ниже главной диагонали системы ЛАУ. Элементарный шаг такого преобразования можно выразить с помощью операции умножения левой и правой части системы на элементарную нижнюю треугольную матрицу вида

(2.4)

Матрицы 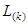отличаются от единичной тем, что 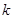-ый столбец данной матрицы, начиная с элемента 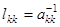, и ниже 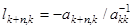, , 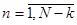формируется специальным образом из соответствующих значений элементов преобразуемой матрицы. В результате умножения

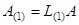(2.5)

преобразованная матрица 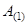будет иметь нулевые значения элементов первого столбца ниже главной диагонали: 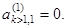Далее, на основе элементов матриц 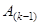, 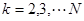последовательно формируются матрицы 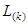и находятся

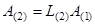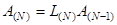, , … . (2.6)

Нетрудно убедиться, что после выполнения описанных действий матрица 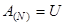будет верхней треугольной матрицей с единицами на главной диагонали.

Таким образом, метод последовательного исключения Гаусса состоит в преобразовании исходной системы уравнений путем умножения ее на элементарные треугольные матрицы, в результате чего исходная система уравнений преобразуется в эквивалентную систему с верхней треугольной матрицей

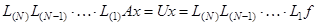. (2.7)

Решение полученной системы уравнений находится с помощью описанного выше алгоритма (2.2), (2.3).

Процедуру (2.5) – (2.7) принято называть прямым ходом метода Гаусса, а (2.2), (2.3) – соответственно обратный ход. Оценим вычислительные затраты прямого и обратного хода метода Гаусса.

Одна операция умножения 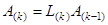имеет вычислительную сложность порядка . В самом деле, каждый элемент матричного произведения находится как скалярное произведение двух векторов, причем вектор первого из сомножителей имеет не более двух ненулевых элементов. В результате каждый из 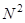элементов матрицы 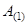вычисляется не более чем за два умножения и одно сложение. Несложно заметить, что в процессе умножения 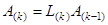элементы матрицы 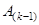, расположенные выше -ой строки и левее -го столбца остаются неизменными: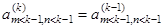. По этой причине вычислительная сложность умножения матриц 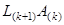уменьшается с ростом 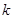и не превосходит 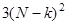. Таким образом, вычислительные затраты на реализацию прямого хода метода Гаусса составляют 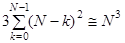операций умножения и сложения. Формирование матриц 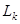требует приблизительно операций. С учетом вышесказанного для матриц достаточно большой размерности 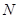можно оценить вычислительную сложность прямого хода метода Гаусса величиной .

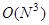Для обратного хода метода Гаусса из выражения (2.3) легко подсчитать, что для вычисления 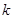-ой компоненты решения требуется 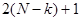операций. Суммирование вычислительных затрат для определения всех 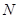неизвестных дает приблизительно 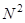операций, что на порядок меньше вычислительной сложности прямого метода Гаусса.

Относительно применимости метода Гаусса можно утверждать, что данный метод является наиболее универсальным в своем классе и может быть использован для решения произвольных систем ЛАУ с неособенной (не вырожденной) матрицей. Тем не менее, источником проблем, с которыми приходится иметь дело при использовании описанного выше алгоритма, являются нулевые (близкие к нулю) значения диагональных элементов, присутствующие в матрице изначально, либо появляющиеся в процессе исключения неизвестных. Как видно из выражения (2.4), при формировании матриц 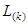выполняется деление на , что в случае 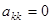приводит к потере корректности алгоритма. Для устранения подобных проблем используется алгоритмы перестановок столбцов (строк) матрицы.