рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Философия
- /
- Свойства собственных значений и собственных векторов матриц.
Реферат Курсовая Конспект
Свойства собственных значений и собственных векторов матриц.
Свойства собственных значений и собственных векторов матриц. - раздел Философия, Численные методы линейной алгебры Пусть Дана Квадратная Невырожденная Матрица ...
Пусть дана квадратная невырожденная матрица 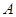 порядка
порядка 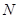 .
.
Число  называется собственным значением матрицы
называется собственным значением матрицы 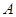 , если существует такой ненулевой вектор
, если существует такой ненулевой вектор 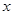 , удовлетворяющий равенству
, удовлетворяющий равенству
 . (4.1)
. (4.1)
Вектор  , удовлетворяющий равенству (4.1), называется собственным вектором матрицы
, удовлетворяющий равенству (4.1), называется собственным вектором матрицы 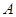 . Совокупность всех собственных значений называется спектром матрицы. Уравнение (4.1) имеет нетривиальные решения тогда и только тогда, когда
. Совокупность всех собственных значений называется спектром матрицы. Уравнение (4.1) имеет нетривиальные решения тогда и только тогда, когда
 . (4.2)
. (4.2)
Функция  называется характеристическим многочленом матрицы. Степень характеристического многочлена равна порядку матрицы, а множество его корней совпадает со спектром. Таким образом, задача поиска собственных значений может быть сведена к задаче вычисления корней характеристического многочлена. Число собственных значений матрицы, с учетом возможной кратности корней характеристического полинома, равно порядку матрицы.
называется характеристическим многочленом матрицы. Степень характеристического многочлена равна порядку матрицы, а множество его корней совпадает со спектром. Таким образом, задача поиска собственных значений может быть сведена к задаче вычисления корней характеристического многочлена. Число собственных значений матрицы, с учетом возможной кратности корней характеристического полинома, равно порядку матрицы.
Спектр действительной матрицы составляют действительные или комплексные числа, образующие комплексно-сопряженные пары. Собственные вектора матрицы определяются с точностью до постоянного множителя. Обычно используют нормированные значения собственных векторов:  . Отметим важные свойства собственных векторов и собственных значений.
. Отметим важные свойства собственных векторов и собственных значений.
1. собственными значениями положительно определенной симметричной матрицы являются действительные положительные числа, причем среди них отсутствуют кратные:  . (4.3)
. (4.3)
2. множество собственных векторов симметричной невырожденной матрицы 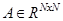 образуют ортогональный базис в пространстве
образуют ортогональный базис в пространстве 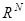 .
.
3. если  – собственное значение матрицы
– собственное значение матрицы 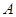 , то
, то  – собственное значение матрицы
– собственное значение матрицы  .
.
4. собственные значения диагональной и треугольной матрицы совпадают с элементами главной диагонали данной матрицы.
5. если  и
и 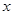 – собственное значение и собственный вектор матрицы
– собственное значение и собственный вектор матрицы 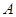 , тогда
, тогда 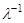 и
и 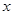 – собственное значение и собственный вектор матрицы
– собственное значение и собственный вектор матрицы 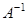 соответственно.
соответственно.
6. для произвольной невырожденной матрицы 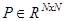 , собственные матрицы
, собственные матрицы 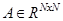 и матрицы
и матрицы  – совпадают. Матрицы
– совпадают. Матрицы 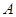 и
и 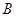 в этом случае называются подобными, а преобразования вида
в этом случае называются подобными, а преобразования вида  называются преобразованиями подобия.
называются преобразованиями подобия.
7.  собственные значения матриц
собственные значения матриц 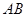 и
и 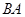 совпадают.
совпадают.
Перечисленные свойства играют важную роль при разработке численных методов решения проблемы собственных значений и собственных векторов. Важно отметить также класс матриц, для которых задача отыскания собственных значений и собственных векторов имеет наиболее простое решение. Это так называемые матрицы простой структуры.
Определение. Если существует невырожденная матрица 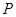 такая, что матрица
такая, что матрица  является диагональной, то матрица
является диагональной, то матрица 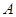 называется матрицей простой структуры.
называется матрицей простой структуры.
Иными словами, матрица простой структуры подобна диагональной матрице, элементами которой являются собственные значения исходной матрицы.
Теорема 4.1. Матрица 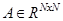 подобна диагональной матрице в том и только в том случае, если она имеет систему
подобна диагональной матрице в том и только в том случае, если она имеет систему 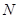 линейно независимых векторов.
линейно независимых векторов.
Доказательство. Докажем вначале, что если все собственные векторы матрицы являются линейно независимыми, то данная матрица – матрица простой структуры. Пусть  ,
,  собственные векторы и собственные значения матрицы
собственные векторы и собственные значения матрицы 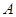 . Пусть матрица
. Пусть матрица 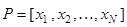 – матрица, столбцами которой являются собственные векторы матрицы
– матрица, столбцами которой являются собственные векторы матрицы 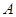 . По определению
. По определению 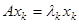 ,
, 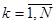 . Последнее равенство для всех
. Последнее равенство для всех 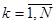 может быть представлено в эквивалентном виде
может быть представлено в эквивалентном виде
 , (4.4)
, (4.4)
где 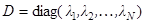 – диагональная матрица элементами которой являются собственные значения. По условию теоремы столбцы матрицы
– диагональная матрица элементами которой являются собственные значения. По условию теоремы столбцы матрицы 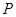 линейно независимы. В силу этого матрица
линейно независимы. В силу этого матрица 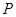 является не вырожденной и существует обратная матрица
является не вырожденной и существует обратная матрица 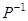 . Умножая равенство (4.4) слева на матрицу
. Умножая равенство (4.4) слева на матрицу 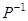 , имеем:
, имеем:
 , (4.5)
, (4.5)
Полученное тождество означает, что матрица 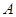 подобна диагональной матрице, что и требовалось доказать.
подобна диагональной матрице, что и требовалось доказать.
Докажем теперь обратное. Пусть матрица 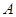 подобна диагональной матрице
подобна диагональной матрице  , элементами которой являются собственные значения матрицы
, элементами которой являются собственные значения матрицы 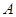 . Тогда выполняется равенство (4.5), умножая которое слева на матрицу
. Тогда выполняется равенство (4.5), умножая которое слева на матрицу 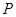 получаем, что в этом случае выполняется и равенство (4.4) . Несложно заметить, что решением матричного уравнения
получаем, что в этом случае выполняется и равенство (4.4) . Несложно заметить, что решением матричного уравнения
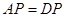 является матрица
является матрица 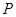 , столбцами которой являются собственные векторы матрицы
, столбцами которой являются собственные векторы матрицы 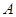 . В силу существования обратной матрицы
. В силу существования обратной матрицы 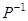 , матрица
, матрица 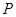 является не вырожденной, откуда следует линейная независимость ее строк и столбцов. Теорема доказана.
является не вырожденной, откуда следует линейная независимость ее строк и столбцов. Теорема доказана.
Упражнения.
1. Доказать, что отношение подобия матриц является отношением эквивалентности.
2. Доказать, что спектральный радиус матрицы не превосходит ее норму.
– Конец работы –
Эта тема принадлежит разделу:
Численные методы линейной алгебры
В М Волков... Численные методы линейной алгебры...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Свойства собственных значений и собственных векторов матриц.
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов