рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Философия
- /
- Лекция 8. ПОНЯТИЕ ФУНКЦИИ
Реферат Курсовая Конспект
Лекция 8. ПОНЯТИЕ ФУНКЦИИ
Лекция 8. ПОНЯТИЕ ФУНКЦИИ - раздел Философия, Лекция 8. ...
Лекция 8.
ПОНЯТИЕ ФУНКЦИИ
Все течет, и все меняется.
Гераклит
ПЛАН 1. Введение. 2. Переменные величины.Таблица 8.1
| Х | 
| х
| х
| 
| … | х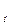
|
| Y | у
| у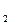
| у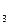
| у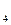
| … | у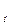
|
Аналитический способ появился с введением систем координат и принятием символической записи различных законов в виде одной формулы  или их совокупности.
или их совокупности.
Иногда функция задается одним аналитическим выражением, например
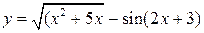 ,
,
или подобными, а иногда несколькими, например, так:

 Наряду с этими двумя способами существует так называемый графический способ задания функции. Говорят, что функция задана графически, если начерчен ее график. Совокупность точек, абсциссы которых являются значениями независимой переменной х, а ординаты – соответствующими значениями функции у, называется графиком данной функции (рис. 8.1).
Наряду с этими двумя способами существует так называемый графический способ задания функции. Говорят, что функция задана графически, если начерчен ее график. Совокупность точек, абсциссы которых являются значениями независимой переменной х, а ординаты – соответствующими значениями функции у, называется графиком данной функции (рис. 8.1).
С момента появления всех трех способов задания функции возникал вопрос о возможности перехода от одного к другому. Для простейших случаев прямой на плоскости или канонических уравнений кривых второго порядка он решался просто – от уравнения переходили к таблице, от таблицы к графику. Этот подход, разработанный математиками 17-18 веков, «работает» до сих пор. Вы с ним знакомились в школе.
Если функция изначально задана аналитически с помощью формулы  , то ее график строят «по точкам». Составляется таблица значений
, то ее график строят «по точкам». Составляется таблица значений
(хn, уn). Точки, имеющие координаты  , наносятся на координатную плоскость, и соединяются плавной линией. Можно считать, что полученная линия является графиком данной функции, но это не всегда правильно. Так как областью определения функции, как правило, является бесконечное множество точек, поэтому невозможно построить график «точно» по точкам, поскольку нельзя нанести на координатную плоскость бесконечное множество точек. А пропуск любой из них может привести к искажению графика. Покажем это на примере.
, наносятся на координатную плоскость, и соединяются плавной линией. Можно считать, что полученная линия является графиком данной функции, но это не всегда правильно. Так как областью определения функции, как правило, является бесконечное множество точек, поэтому невозможно построить график «точно» по точкам, поскольку нельзя нанести на координатную плоскость бесконечное множество точек. А пропуск любой из них может привести к искажению графика. Покажем это на примере.
Пример 8.1.Построить графикфункции 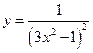 по точкам.
по точкам.
Решение. Составим таблицу частных значений аргумента и соответствующих им значений функции.
| хn | –3 | –2 | –1 | ||||
| yn | 
| 
| 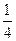
| 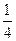
| 
| 
|
Рассмотрение полученной таблицы показывает, что на интервале (–3,0) значение у возрастает, а на интервале (0, 3) – убывает симметрично, поэтому и график функции предположительно будет симметричен относительно оси ОХ. (рис. 8.2а).
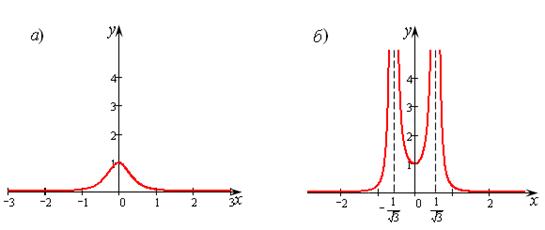
Рис. 8.2
Но в таблице не отражен факт, что при  функция не определена, а при х = 0,5 у = 16, поэтому правильный график этой функции приведен на рис. 8.2б.
функция не определена, а при х = 0,5 у = 16, поэтому правильный график этой функции приведен на рис. 8.2б.
Обычно построение графика функции производится на основании исследования функции и только для уточнения определяется некоторое количество его точек.
Еще более трудной задачей оказался обратный ход в цепочке формула-таблица-график. Уже составление таблицы по данным графика приводило к погрешностям, а уж построением уравнения связи занимаются до сих пор и не всегда успешно.
Есть ли преимущества одного способа задания функции перед другим, и какой из них важнее для экономистов? Так как полем действия экономистов являются числа и таблицы, то на первый взгляд кажется, что следует остановиться именно на табличном способе, а остальные отбросить. Но график функции нагляднее показывает любое изменение, а короткая формула содержит в себе и таблицу и график. Надо знать все три и применять их по мере надобности. Знаний лишних не бывает. Поэтому будем рассматривать все характеристики функций с трех сторон. Как бы не была задана функция, в любом случае:
Функция – это закон (правило), по которому каждому элементу Х из множества М соответствует единственный элемент Y из множества L.
1) Закон может быть задан аналитически, таблично или графически.
2) Множество значений х  М,каждое из которыхприводит к действительным значенияму, называется областью определенияфункции или областью ее существования.
М,каждое из которыхприводит к действительным значенияму, называется областью определенияфункции или областью ее существования.
3) Множество действительных значений 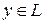 называется областью изменения самой функции.
называется областью изменения самой функции.
Функции, отвечающие этому определению, называются однозначными. Если одному значению Х соответствует два или несколько значений Y, такие функции называются многозначными (рис. 8.3).

Рис. 8.3
8.4. Область определения функции
Область определения функции может быть отрезком, интервалом и всей числовой осью. Это зависит от вида функции и способа ее задания.
Если функция задана таблично, то областью ее существования будет являться перечень всех значений х.
Например, пусть функция задана таблицей, где х – затраты на производство, у – прибыль:
Таблица 8.2
| Х (млн. руб.) | 1,05 | 1,07 | 1,09 | 1,4 | 1,8 | 2,0 |
| Y (млн. рyб.) | 7,54 | 9,56 | 11,67 | 13,90 | 12,73 | 8,09 |
Поскольку в таблице нет указаний на то, что какая-то точка не вошла в рассмотрение, то областью существования этой функции можно считать отрезок [1,05; 2,0].
Если функция задана графически, то нахождение области ее определения так же не составляет труда. Например, функция, изображенная на рис. 8.4а определена на интервале
(–5, 1), а на рис. 8.4б – на объединении двух полуинтервалов [–4,5)È(5,8].
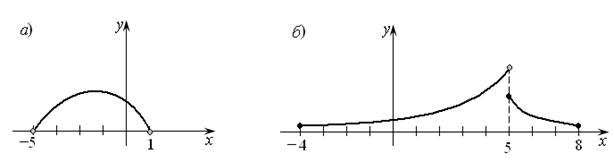
Рис. 8.4
Если функция задана аналитически, с помощью одного или нескольких выражений, то исследование области ее существования определяется не только естественной областью, на которой она существует, но и заданием. Например, функция 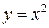 естественной областью определения имеет интервал
естественной областью определения имеет интервал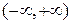 . Но, эта же самая функция также может быть задана на отрезке
. Но, эта же самая функция также может быть задана на отрезке 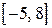 и на любом другом промежутке.
и на любом другом промежутке.
Естественная область существования функции исключает точки, где знаменатель равен нулю, подкоренное выражение для четных радикалов отрицательно, выражение, стоящее под знаком логарифма – неположительно, и т.д.
1) Функция  имеет областью определения отрезок
имеет областью определения отрезок 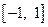 , где подкоренное выражение неотрицательно.
, где подкоренное выражение неотрицательно.
2) Функция  определена на двух полуинтервалах [–1, 0) и (0, 1].
определена на двух полуинтервалах [–1, 0) и (0, 1].
3) Функция 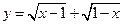 определена только при х = 1, так как первое слагаемое определено на полуинтервале [1,
определена только при х = 1, так как первое слагаемое определено на полуинтервале [1,  , а второе – на
, а второе – на 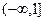 . Их объединение и дает точку
. Их объединение и дает точку
х = 1.
4) Функция 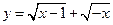 не определена ни при каком х, так как
не определена ни при каком х, так как 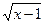 существует при
существует при  , а
, а  – если
– если  .
.
8.5. Область значений функции
Область значений функцииyилиобласть ее изменения показывает, в каких пределах изменяется сама функция.
Если функция задана таблично, то область ее изменений находят по наименьшему и наибольшему значениям для у. В нашем случае – это пределы от 7,54 до 13,90 млн. руб. (табл. 8.2).
Если функция задана графически – так же находят границы по ординате, проводя прямые, параллельные оси ОХ до пересечения с остью ОY, точек, в которых у принимает наибольшее и наименьшее значения.
Нахождение области изменения функции, заданной аналитически, решается в каждом конкретном случае отдельно. Например:
1) Функция 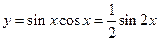 может принимать значения, удовлетворяющие условию
может принимать значения, удовлетворяющие условию  , т.к.
, т.к.  , и множитель 1/2 уменьшает отрезок [–1, 1] вдвое. Аргумент х принимает любые значения:
, и множитель 1/2 уменьшает отрезок [–1, 1] вдвое. Аргумент х принимает любые значения: 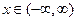 .
.
2) Функция 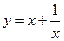 может принимать значения
может принимать значения  при условии, что
при условии, что 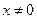 . Действительно, разрешим это уравнение относительно переменной х. Как это делается?
. Действительно, разрешим это уравнение относительно переменной х. Как это делается?
а) Приведем все к общему знаменателю, получим: 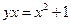 или
или  .
.
б) Выделим полный квадрат по х:
 , или
, или 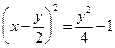 .
.
3) Извлечем корень квадратный из левой и правой части:
 .
.
4) Найдем х:
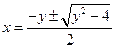 .
.
Для того, чтобы х принимал действительные значения, необходимо, чтобы 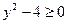 , откуда
, откуда  , что и требовалось доказать.
, что и требовалось доказать.
(Не самая простая задача, но иногда ее решение дает большую пользу).
Если областью значений функции являются все значения (–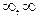 ), то ее называют неограниченной. Если
), то ее называют неограниченной. Если 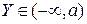 , то ее называют ограниченной сверху,
, то ее называют ограниченной сверху,  , то она ограничена снизу и если
, то она ограничена снизу и если 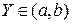 то ее называют просто ограниченной (рис.8.6).
то ее называют просто ограниченной (рис.8.6).

Рис. 8.5
Если функция задается несколькими выражениями, например, так:
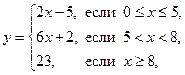
то область допустимых значений находится по заданию, а область значений функции по оценке наибольших и наименьших значений для каждой составляющей функции.
В данном случае х изменяется от 0 до 8, а у – от –5 до 50. Проверьте правильность наших рассуждений самостоятельно, составив таблицы соответствующих функций и построив их графики.
Напомним, что функции могут быть четными, нечетными и общего вида.
Функция называется четной, если для нее выполняется равенство:  , и нечетной, если
, и нечетной, если  . Четная функция симметрична относительно оси ОY, нечетная – относительно начала координат.
. Четная функция симметрична относительно оси ОY, нечетная – относительно начала координат.
Примером четной функции является степенная функция вида  , т.е. с четным показателем степени, а нечетная – с нечетным показателем степени –
, т.е. с четным показателем степени, а нечетная – с нечетным показателем степени –  .
.
Кроме того, функции могут быть периодическими и непериодическими. Функция называется периодической, если существует такое положительное число Т, что для всех x из области определения, выполняется равенство: 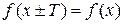 .К периодическим, в основном, относятся тригонометрические функции, или функции, заданные специальным образом. Из школьного курса известно, что
.К периодическим, в основном, относятся тригонометрические функции, или функции, заданные специальным образом. Из школьного курса известно, что  ,
, 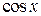 имеют минимальный период, равный 2
имеют минимальный период, равный 2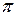 , а
, а 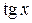 ,
, 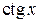 – период
– период 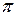 .
.
8.6. Основные элементарные функции
К основным элементарным функциям относятся следующие:
1. Степенная функция 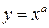 , где a – действительное число.
, где a – действительное число.
2. Показательная функция  , где а – положительное число, не равное единице.
, где а – положительное число, не равное единице.
3. Логарифмическая функция: 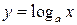 , где основание логарифмов а – положительное число, не равное единице.
, где основание логарифмов а – положительное число, не равное единице.
4. Тригонометрические функции:  ,
, 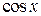 ,
, 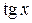 ,
, 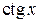 .
.
5. Обратные тригонометрические функции: 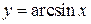 ,
, 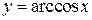 ,
, 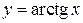 ,
,  .
.
Графики всех функций приведены ниже (см. рис. 8.6-10). Эти функции достаточно хорошо изучались в школе.
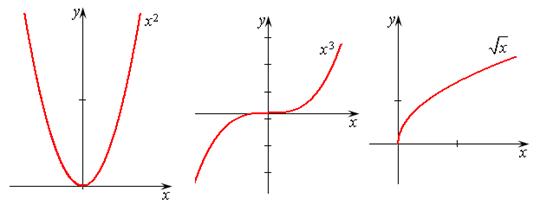

Рис.8.6.Степенные функции
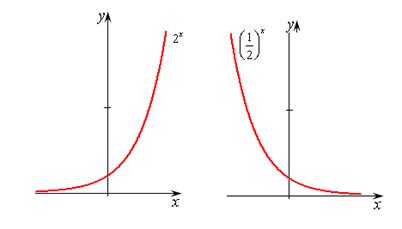
Рис.8.7.Показательные функции

Рис.8.8.Логарифмические функции
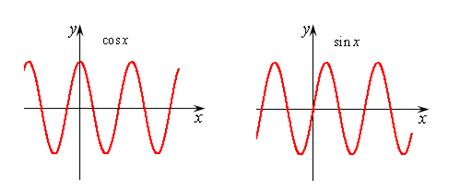

Рис.8.9.Тригонометрические функции

Рис.8.10.Обратные тригонометрические функции
Элементарной функцией называется функция, которая может быть помощи конечного числа основных элементарных функций при помощи основных арифметических действий и взятия функции от функций.
Примеры элементарных функций:
 ,
, 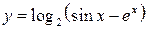 .
.
Примеры неэлементарных функций:
 – целая часть x,
– целая часть x, 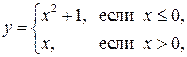
 .
.
С последней функцией мы еще встретимся при изучении теории вероятностей.
В свою очередь элементарные функции делятся на алгебраические и неалгебраические (трансцендентные).
Алгебраической называется функция, в которой над аргументом проводится конечное число арифметических действий. К числу алгебраических относятся:
1) целая рациональная функция (многочлен или полином):
 ;
;
2) дробно-рациональная функция – отношение двух многочленов;
3) иррациональная функция – функция, полученная путем конечного числа арифметических действий и операции функции от функции над степенными функциями с целыми и дробными показателями и не являющаяся рациональной, например
 ,
, 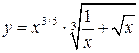 .
.
Всякая неалгебраическая функция называется трансцендентной. К числу трансцендентных функций относятся функции: показательная, логарифмическая, тригонометрическая, обратная тригонометрическая.
8.7. Заключение
Мы будем изучать разные функции. Это изучение имеет не только познавательный, но и практический смысл, как и все, о чем мы говорили раньше.
Первые выводы:
1) Функция – это закон, связывающий две переменные величины.
2) Функцию можно задать таблично, графически, аналитически.
3) Для каждой функции определяется область определения и область значений.
Фундаментальное значение для дальнейшего рассмотрения поведения функций играет понятие предела.
Лекция 9.
ПРЕДЕЛ ФУНКЦИИ
И долго я блуждал, и часто утомленный
Я думал о тебе, предел благословенный.
А.С. Пушкин
ПЛАН
1. Введение.
2. Определение предела функции.
3. Бесконечно малые функции. Ограниченные функции
4. Бесконечно большие функции и их связь с бесконечно малыми
5. Сравнение бесконечно малых функций
6. Основные теоремы о пределах.
7. Техника раскрытия неопределенностей.
8. Первый замечательный предел
9. Второй замечательный предел
10. Начисление непрерывных процентов
9.1. Введение
Анализ продаж за три года показал следующую зависимость прибыли Y (млн. руб.) от времени Х, измеряемого в месяцах. Экономист предприятия свел данные в таблицу (см. табл. 9.1) и нарисовал график изменения Y от Х (см. рис. 9.1).
Таблица 9.1
| Х (месяцы) | ||||
| Y (млн. руб.) | 1,5 | 1,75 | 1,99 | 1,999 |
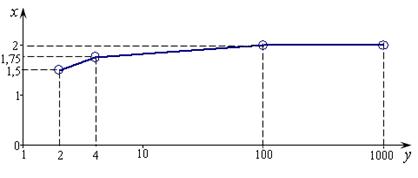
Рис. 9.1
Аналитическое выражение этой функциональной зависимости может быть определено как 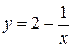 , где х – время, у – прибыль. (Подставьте в нее значения аргумента – получите значение функции).
, где х – время, у – прибыль. (Подставьте в нее значения аргумента – получите значение функции).
Рассматривая таблицу и график можно предположить, что с возрастанием аргумента х эта функция неограниченно будет приближаться к числу 2, или, как говорят, имеет при х пределом число 2. Вывод: если предприятие ничего не изменит при продажах своей продукции, ее прибыль не сможет стать больше 2 млн. руб.
пределом число 2. Вывод: если предприятие ничего не изменит при продажах своей продукции, ее прибыль не сможет стать больше 2 млн. руб.
Отвлечемся от конкретной экономической задачи и рассмотрим ее в общем виде.
9.2. Определение предела функции
Пусть М(х, у) – текущая точка на графике функции  . Найдем расстояние от точки М до прямой у = 2.
. Найдем расстояние от точки М до прямой у = 2.
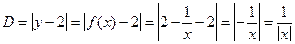 .|
.|
Это расстояние зависит от х и может быть сделано меньше любого положительного наперед заданного числа для достаточно больших х. Так, например, 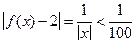 , если х > 100,
, если х > 100,
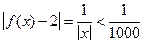 , если х > 1000,
, если х > 1000,
И вообще, если 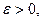 то
то 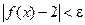 , если
, если  .
.
Введем определение предела функции при различных устремлениях Х.
Предел функции при.
Это значит, что при неограниченном возрастании х функция сколь угодно мало отличается от числа b и на чертеже ординаты графика функции попадают в… Символическая запись предела функции выглядит так: .Рис. 9.3
Пример 9.1. Доказать, что 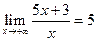 .
.
Решение. Следуя определению предела, зададим произвольное число 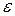 и составим абсолютную величину разности
и составим абсолютную величину разности
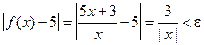 .
.
Это неравенство будет выполняться для любых x, больших чем 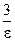 .
.
2. Предел функции при 
Определение 9.2. Число b называется пределом функции при  , если для любого положительного числа
, если для любого положительного числа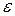 найдется такое число
найдется такое число  , что для всех
, что для всех 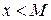 выполняется неравенство
выполняется неравенство 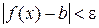 .
.
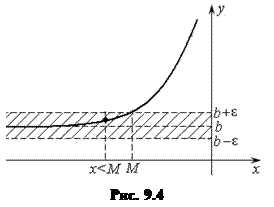 Геометрический смысл предела функции при х аналогичен геометрическому смыслу при
Геометрический смысл предела функции при х аналогичен геометрическому смыслу при 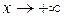 (рис. 9.4).
(рис. 9.4).
Символическая запись предела функции выглядит так:
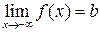 .
.
Следующие определения традиционно является одними из самых трудно понимаемых и воспроизводимых студентами определений.
Предел функции при слева, справа, двусторонний предел
Геометрически это означает следующее: ординаты точек графика попадут в полосу, ограниченную прямыми у =b –и у = b + , как только x станет больше,… Символическая запись левостороннего предела функции выглядит так: .Рис. 9.5 Рис. 9.6
Определение 9.4.Число b называется пределом функции при  справа (
справа (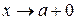 ), если для любого положительного числа
), если для любого положительного числа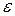 найдется такое число M, что для всех х, таких что
найдется такое число M, что для всех х, таких что  выполняется неравенство
выполняется неравенство 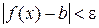 .
.
Геометрическая интерпретация остается прежней: точки графика функции попадут в полосу, ограниченную прямыми у = b – 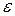 и у = b+
и у = b+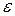 , для всех х, заключенных между a и М (рис. 9.6).
, для всех х, заключенных между a и М (рис. 9.6).
Символическая запись правостороннего предела функции выглядит так:
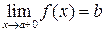 .
.
Пределы функции при  слева и справа называются односторонними пределами. Мы с ними встретимся, когда будем проходить тему «Непрерывность функции в точке».
слева и справа называются односторонними пределами. Мы с ними встретимся, когда будем проходить тему «Непрерывность функции в точке».
Если оба односторонних предела существуют и равны между собой, то говорят, что функция имеет предел при  . Определение предела функции в точке
. Определение предела функции в точке 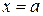 звучит так.
звучит так.
Определение 9.5. Число b называется пределом функции при  , если для любого положительного числа
, если для любого положительного числа 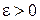
 найдется такое число
найдется такое число 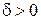 , что для всех х, таких что
, что для всех х, таких что 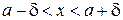 , будет выполняться неравенство
, будет выполняться неравенство 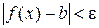 .
.
Покажем некоторые логические символы, которые можно применять для более краткой записи этих определений.
Символ  означает «для всех», «для каждого», «какого бы ни было». Например, запись
означает «для всех», «для каждого», «какого бы ни было». Например, запись 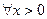 означает «для любого х > 0».
означает «для любого х > 0».
Символ 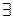 х означает «существует такое х» или «можно найти такое х». Запись
х означает «существует такое х» или «можно найти такое х». Запись  означает «существует такое положительное число х».
означает «существует такое положительное число х».
Символ принадлежности  : х
: х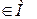 . Символы логического следствия
. Символы логического следствия  .Знак логической равносильности
.Знак логической равносильности 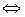 . Их вы знаете из школы.
. Их вы знаете из школы.
Запись 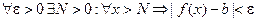 означает: каково бы ни было число
означает: каково бы ни было число 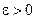 , существует такое число
, существует такое число 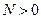 , что для любого
, что для любого 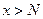 имеет место неравенство
имеет место неравенство  .
.
Можно доказать, что если функция имеет предел, то он единственный.
9.3. Бесконечно малые функции. Ограниченные функции
Введем новый класс функций, имеющих большое значение в математическом анализе – бесконечно малые и бесконечно большие величины.
Определение 9.6. Функция  называется бесконечно малой при
называется бесконечно малой при  , если
, если 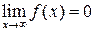 .
.
Примерами бесконечно малых функций при  являются функции
являются функции 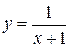 ,
,  и другие.
и другие.
Аналогично можно ввести определение бесконечно малой величины при  или
или  . Например, функции
. Например, функции  ,
,  являются бесконечно малыми при
являются бесконечно малыми при  . Функции
. Функции 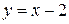 ,
,  являются бесконечно малыми при
являются бесконечно малыми при 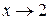 .
.
Определение 9.7. Функция  называется ограниченной на некотором множестве М значений аргумента х, если существует такое положительное число С, что для всех
называется ограниченной на некотором множестве М значений аргумента х, если существует такое положительное число С, что для всех  выполняется неравенство
выполняется неравенство 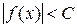 .
.
Понятие бесконечно малой и ограниченной функции только на первый взгляд кажутся похожими. Например, функция  при
при  не имеет предела, она ограничена сверху числом
не имеет предела, она ограничена сверху числом 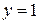 и снизу
и снизу 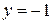 .
.
Дадим несколько утверждений, касающихся действий над бесконечно малыми величинами. Их доказательство можно найти в учебниках. Все утверждения дадим в предположении, что х , так как в остальных случаях формулировки будут аналогичными.
, так как в остальных случаях формулировки будут аналогичными.
Утверждение 1. Сумма конечного числа бесконечно малых величин есть величина бесконечно малая.
(А бесконечного числа бесконечно малых величин?)
Утверждение 2. Произведение бесконечно малой величины на число k есть величина бесконечно малая.
Утверждение 3. Произведение двух бесконечно малых функций есть функция бесконечно малая.
Утверждение 4. Произведение бесконечно малой функции на ограниченную есть функция бесконечно малая.
Прежде, чем давать определение частного двух бесконечных величин, введем понятие бесконечно больших величин.
9.4. Бесконечно большие функции и их связь с бесконечно малыми
Определение 9.8.Функция  называется бесконечно большой при
называется бесконечно большой при  или
или  , если ее предел равен –
, если ее предел равен –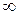 или +
или +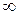 .
.
Примерами бесконечно большой функции при  являются функции
являются функции 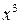 ,
,  .
.
Функции  ,
, 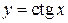 являются бесконечно большими при
являются бесконечно большими при 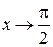 и
и  соответственно, а
соответственно, а  – бесконечно большая при
– бесконечно большая при  .
.
Утверждения 1-4 остаются в силе и для бесконечно больших величин.
Введем еще два утверждения.
Утверждение 5.Величина, обратная бесконечно большой, есть величина бесконечно малая.
Утверждение 6.Величина, обратная бесконечно малой, есть величина бесконечно большая.
Бесконечно малые величины будем обозначать a1, a2 или б.м.в., бесконечно большие – b1, b2 или б.б.в.
Следующие примеры являются гимнастикой для ума.
Пример 9.2. Будет ли величина, равная  +7 бесконечно малой?
+7 бесконечно малой?
Решение. Нет, т.к. сумма первых трех слагаемых будет бесконечно малой величиной, стремящейся к нулю, но последнее слагаемое 7 – постоянное число, поэтому общая сумма будет равна 7.
Пример 9.3. Будет ли величина  величиной б.б.в? Или б.м.в.?
величиной б.б.в? Или б.м.в.?
Решение. Первое, третье и последнее слагаемые будут б.м.в., а второе и четвертое – бесконечно большими, причем понятно, что произведение б.б.в. больше одного из сомножителей. Поэтому вся величина есть бесконечно большая.
Итак, с суммой и произведением б.б.в. и б.м.в. понятно. И даже с разностью бесконечно малых величин – тоже, потому что из соображений здравого смысла можно ожидать, что разность двух бесконечно малых величин есть величина бесконечно малая. Но разность бесконечно больших величин уже не определяется так просто. Например, величина 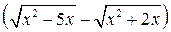 при
при  будет б.б.в., б.м.в. или обычной величиной? Пока трудно сказать. Введем дополнительные определения, позволяющие сравнивать их по порядку великости, а бесконечно малые величины – по порядку малости.
будет б.б.в., б.м.в. или обычной величиной? Пока трудно сказать. Введем дополнительные определения, позволяющие сравнивать их по порядку великости, а бесконечно малые величины – по порядку малости.
Порядок малости и великости величины x определяется положительной степенью, в которую она возводится.
Например, x3 имеет третий порядок малости при x→0, а  – бесконечно большая величина второго порядка великости при x→∞.
– бесконечно большая величина второго порядка великости при x→∞.
9.5. Сравнение бесконечно малых функций
Определение 9.9.Две бесконечно малые функции 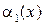 и
и 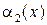 в окрестности точки a называются эквивалентными, если предел их отношения при
в окрестности точки a называются эквивалентными, если предел их отношения при  равен 1:
равен 1:
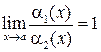 .
.
Например, функции  и
и  будут эквивалентными б.м.в. при
будут эквивалентными б.м.в. при  , потому что
, потому что 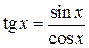 будет эквивалентен
будет эквивалентен  , т.к.
, т.к. 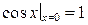 .
.
Определение 9.10. Две бесконечно малые функции 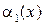 и
и 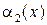 называются б.м.в. одного порядка малости, если предел их отношения равен числу, не равного нулю:
называются б.м.в. одного порядка малости, если предел их отношения равен числу, не равного нулю:
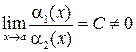 .
.
Например, х и 3х при  будут одного порядка малости, т.к.
будут одного порядка малости, т.к. 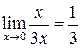 .
.
Определение 9.11. Функция 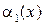 называется бесконечно малой более высокого порядка малости, чем
называется бесконечно малой более высокого порядка малости, чем 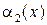 , если предел их отношения равен нулю:
, если предел их отношения равен нулю:
 .
.
Функция 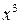 будет иметь третий порядок малости относительно x, а х – первый при
будет иметь третий порядок малости относительно x, а х – первый при  , поэтому предел их отношения
, поэтому предел их отношения 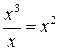 будет равен нулю, т.е.
будет равен нулю, т.е. 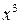 является б.м.в. более высокого порядка малости, чем x:
является б.м.в. более высокого порядка малости, чем x:
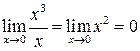 .
.
Определение 9.12.Функция 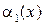 называется бесконечно малой более низкого порядка малости чем
называется бесконечно малой более низкого порядка малости чем 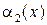 , если предел их отношения равен
, если предел их отношения равен 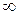 :
:
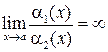 .
.
Функция х будет иметь первый порядок малости при  , а
, а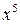 – пятый, поэтому предел их отношения
– пятый, поэтому предел их отношения 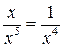 будет равен бесконечности:
будет равен бесконечности:
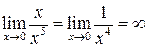 .
.
Сравнение бесконечно больших функций вводится аналогично.
Определение 9.13. Две бесконечно большие функции 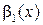 и
и 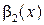 в окрестности точки a называются эквивалентными, если предел их отношения при
в окрестности точки a называются эквивалентными, если предел их отношения при  равен 1:
равен 1:
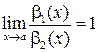 .
.
Например, функции 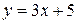 и
и 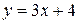 будут эквивалентными при
будут эквивалентными при  , так как их отношение будет равно единице. Действительно,
, так как их отношение будет равно единице. Действительно, 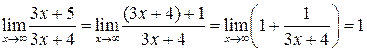 , потому что второе слагаемое есть величина бесконечно малая.
, потому что второе слагаемое есть величина бесконечно малая.
Определение 9.14. Две бесконечно большие функции 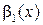 и
и 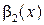 называются б.б.в. одного порядка великости, если предел их отношения равен числу, не равного нулю:
называются б.б.в. одного порядка великости, если предел их отношения равен числу, не равного нулю:
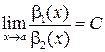 .
.
Так, функции 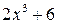 и
и 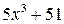 будут одного порядка великости, т.к.
будут одного порядка великости, т.к.  .
.
Определение 9.15. Функция 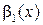 называется б.б.в. более высокого порядка великости, чем
называется б.б.в. более высокого порядка великости, чем 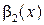 , если предел их отношения равен
, если предел их отношения равен 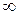 :
:
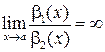 .
.
Например, 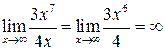 , то
, то 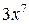 является б.б.в. более высокого порядка великости, чем 4x.
является б.б.в. более высокого порядка великости, чем 4x.
Определение 9.16.Функция 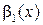 называется б.б.в. более низкого порядка великости чем
называется б.б.в. более низкого порядка великости чем 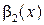 , если предел их отношения равен нулю:
, если предел их отношения равен нулю:
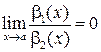 .
.
Функции 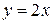 и
и 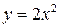 будут отвечать этому условию при
будут отвечать этому условию при  , потому что степень первой функции равна единице, а второй – двум. Предел их отношения
, потому что степень первой функции равна единице, а второй – двум. Предел их отношения 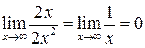 . Следовательно, 2x – б.б.в. более низкого порядка великости, чем
. Следовательно, 2x – б.б.в. более низкого порядка великости, чем  .
.
Зная определение бесконечно малой величины, введем новое определение предела функции, которое поможет нам сформулировать основные теоремы о пределах.
Определение 9.17. Если функцию  при стремлении
при стремлении  (или к любому другому пределу) можно представить в виде суммы числа b и бесконечно малой величины
(или к любому другому пределу) можно представить в виде суммы числа b и бесконечно малой величины 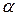 , то число b называется пределом функции f(x) при
, то число b называется пределом функции f(x) при  , т.е.
, т.е.  .
.
В этом определении роль наперед заданной величины 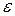 из первого определенияиграет
из первого определенияиграет 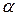 . Она может быть больше нуля, и тогда функция будет стремиться к своему пределу, оставаясь больше него, т.е. сверху (см. рис. 9.6а). Если
. Она может быть больше нуля, и тогда функция будет стремиться к своему пределу, оставаясь больше него, т.е. сверху (см. рис. 9.6а). Если  , то функция стремится к числу b снизу, оставаясь меньше него (см. рис. 9.6б).
, то функция стремится к числу b снизу, оставаясь меньше него (см. рис. 9.6б).
Последнее определение позволяет заменять выражение, стоящее под знаком предела, его предельным значением, т.е. вместо x подставлять его предел. Например,  .
.
Этоже определение позволяет сформулировать и доказать основные теоремы о пределах.
9.6. Основные теоремы о пределах
Если существуют пределы 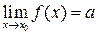 ,
,  , то:
, то:
1. ,илипредел суммы двух функций равен сумме пределов этих функций.
,илипредел суммы двух функций равен сумме пределов этих функций.
2.  ,или предел произведения двух функций равен произведению пределов этих функций.
,или предел произведения двух функций равен произведению пределов этих функций.
3. 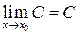 , илипредел постоянной величины равен самой постоянной.
, илипредел постоянной величины равен самой постоянной.
4. , илипостоянную величину можно выносить за знак предела.
, илипостоянную величину можно выносить за знак предела.
5. 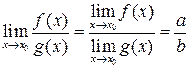 ,илипредел частного двух функций равен частному пределов этих функций, при условии, что предел знаменателя отличен от нуля.
,илипредел частного двух функций равен частному пределов этих функций, при условии, что предел знаменателя отличен от нуля.
6.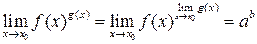 , илипредел степени равен степени предела.
, илипредел степени равен степени предела.
Доказательство этих теорем предлагаем провести самостоятельно, основываясь на втором определении предела и учитывая, что предел бесконечно малой величины равен нулю.
Пример 9.4.Вычислить пределы функций:
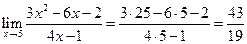 ,
,  .
.
К сожалению, эти теоремы мало помогают, если выражение, стоящее под знаком предела стремится к бесконечности или нулю, и в результате получаем неопределенности типа 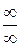 ,
,  ,
,  . Рассмотрим технику вычисления подобных примеров. Ее называют техникой раскрытия неопределенностей.
. Рассмотрим технику вычисления подобных примеров. Ее называют техникой раскрытия неопределенностей.
9.7. Техника раскрытия неопределенностей типа 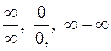
При раскрытии неопределенностей первых двух типов полезно знать следующие теоремы, доказательства которых основываются на свойствах бесконечно малых и бесконечно больших функций.
Теорема 9.1. Сумма конечного числа бесконечно больших функций различных порядков эквивалентна слагаемому наибольшей степени великости.
Теорема 9.2. Сумма конечного числа бесконечно малых функций различных порядков эквивалентна слагаемому наименьшей степени малости.
О чем говорят эти теоремы? Нужно выбирать наибольшие слагаемые, а остальные можно отбросить.
Докажем первую теорему.
Рассмотрим предел суммы бесконечно больших величин при  . Вынесем член с наибольшей степенью за скобки. Тогда все остальные разделятся на него, и из бесконечно больших превратятся в бесконечно малые. Их предел равен нулю. Под знаком предела останется только член, который мы первоначально вынесли, что и требовалось доказать. Например,
. Вынесем член с наибольшей степенью за скобки. Тогда все остальные разделятся на него, и из бесконечно больших превратятся в бесконечно малые. Их предел равен нулю. Под знаком предела останется только член, который мы первоначально вынесли, что и требовалось доказать. Например,
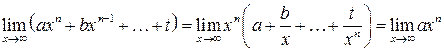 .
.
Пример 9.4.
1)  . 2)
. 2) 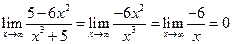 .
.
3)  . 4)
. 4) 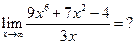
Какой можно сделать вывод из рассмотренных примеров?
Предел частного двух многочленов с разными степенями великости при x→∞ будет равен:
а) числу, если их степени равны;
б) нулю, если степень знаменателя выше степени числителя;
в) бесконечности, т.е. не существует, если степень числителя выше степени знаменателя.
Аналогично рассматриваются примеры отношения бесконечно малых величин, когда мы имеем неопределенность вида  . В данном случае следует оставлять члены с наименьшей степенью, так как именно они будут вносить наибольший вклад в общую сумму.
. В данном случае следует оставлять члены с наименьшей степенью, так как именно они будут вносить наибольший вклад в общую сумму.
5) 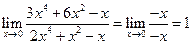 . 6)
. 6) 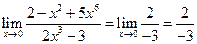 . 7)
. 7) 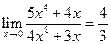 .
.
Рассмотрим еще один пример на неопределенность типа 0/0.
8) 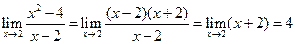 .
.
Почему стало возможным сократить на «нулевой» множитель? Потому что х только стремится к 2, но никогда его не достигает, между ним и 2 всегда есть «зазор» – бесконечно малая величина, которую сократить можно.
Рассмотрим последний тип неопределенности 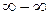 , означенный в заголовке на примере.
, означенный в заголовке на примере.
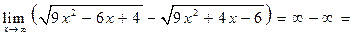
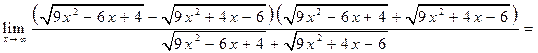
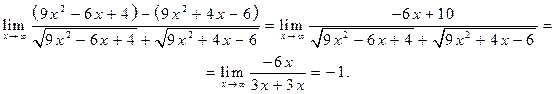
Здесь мы применили искусственный прием – умножили и разделили на множитель, сопряженный данному выражению, а потом к получившейся дроби применили то же правило выделения «старшего слагаемого», который рассмотрели выше.
Рассмотрим еще два предела, которые получили название замечательных в силу неожиданности ответа.
9.8. Первый замечательный предел
Рассмотрим две теоремы, которые нам понадобятся при выводе формулы первого замечательного предела.
Теорема 9.3.Пусть даны три функции f(x), g(x), h(x), связанные неравенствами f(x) < g(x) < h(x), причем функции f(x) и h(x) стремятся к одному пределу b при  (или
(или  ). Тогда и функция g(x) также будет стремиться к числу b при
). Тогда и функция g(x) также будет стремиться к числу b при  (
( ).
).
Математики шутливо называют эту ее теоремой о двух милиционерах.
Иллюстрацией этой теоремы служит рис. 9.7.

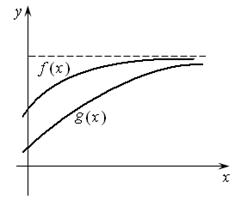
Рис. 9.7 Рис. 9.8
Теорема 9.4.Пусть функции f(x) и g(x), связанные неравенством f(x)>g(x), имеют пределы при х (х
(х ). Тогда
). Тогда  (рис. 9.8).
(рис. 9.8).
Используем эти теоремы для определения предела 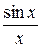 при
при  .
.
Эта функция не определена при х®0, т.к. знаменатель дроби обращается в нуль. Рассмотрим окружность радиуса 1 (рис.9.9). Обозначим центральный угол МОA через x. Будем считать х лежит в первой четверти. Из рисунка следует, что площадь треугольника МОА меньше площади сектора МОА и меньше площади треугольника СОА:
МОА меньше площади сектора МОА и меньше площади треугольника СОА:

 ,
,
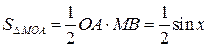 ,
,
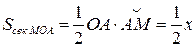 ,
,
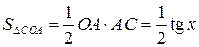 .
.
После сокращения на ½ неравенство перепишется так:
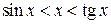
Разделим на  , в результате получим
, в результате получим
 ,
,
т.к. 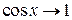 при
при  .
.
Итак, с одной стороны отношение 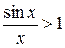 , а с другой – меньше. На основании теоремы 9.3 приходим к выводу, что предел этого отношения равен 1, т.е.
, а с другой – меньше. На основании теоремы 9.3 приходим к выводу, что предел этого отношения равен 1, т.е.
 (9.1)
(9.1)
Это и есть формула первого замечательного предела.
Обсудим ее. При стремлении х к нулю и числитель, и знаменатель стремятся к нулю, т.е. являются бесконечно малыми величинами. Так как их отношение равно 1, то по определению 9.9, они являются эквивалентными бесконечно малыми величинами и при вычислении пределов частного одну из них можно заменять на другую. Это дает большое преимущество при решении примеров. Запишем еще несколько эквивалентных пар:
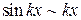 ,
, 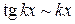 ,
, 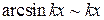 ,
,  .
.
Пример 9.5. Вычислить предел функции
 .
.
В числителе дроби произвели замену тригонометрических функций на эквивалентные, в знаменателе вспомнили, что слагаемое 2х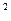 б.м.в. более высокого порядка малости, чем 5х, и его можно отбросить (по теореме 9.2).
б.м.в. более высокого порядка малости, чем 5х, и его можно отбросить (по теореме 9.2).
Если одна из эквивалентных величин возводится в степень, то и другая – тоже, т.е.  .
.
9.9. Второй замечательный предел. Число e
Рассмотрим переменную величину  , где n – переменная, принимающая значения из натурального ряда чисел: 1, 2, 3, ...
, где n – переменная, принимающая значения из натурального ряда чисел: 1, 2, 3, ...
Ее значениями будут числа (1+1), (1+1/2)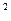 , (1+1/3)
, (1+1/3)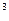 , …. , т.е. наименьшим значение будет число 2, а наибольшее не превышает 3. Проверьте это утверждение на калькуляторе, давая n различные значения (не забывайте про степень). При стремлении n в бесконечность, предел, к которому будет стремиться данное выражение, будет выражаться иррациональным числом
, …. , т.е. наименьшим значение будет число 2, а наибольшее не превышает 3. Проверьте это утверждение на калькуляторе, давая n различные значения (не забывайте про степень). При стремлении n в бесконечность, предел, к которому будет стремиться данное выражение, будет выражаться иррациональным числом
е = 2,7182818284…, которое получило название числа Эйлера. А сам предел получил название второго замечательного предела.
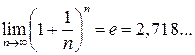 (9.2)
(9.2)
Доказательство этого факта можно найти в рекомендуемой литературе по математическому анализу.
Показательная функция с основанием е: 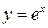 играет большую роль не только в математике, физике, но и экономике, что вы увидите при изучении экономической теории. Мы это увидим на примере начисления непрерывных процентов.
играет большую роль не только в математике, физике, но и экономике, что вы увидите при изучении экономической теории. Мы это увидим на примере начисления непрерывных процентов.
Логарифмы, в основании которых лежит число e, называют натуральными логарифмами. Их значения сведены в таблицу и могут быть найдены с помощью калькуляторов. Свойства натуральных логарифмов аналогичны свойствам остальных логарифмов:
1) 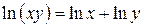 , 2)
, 2) 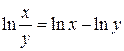 , 3)
, 3) 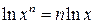 , 4)
, 4) 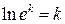 .
.
Обратите внимание, что в формуле второго замечательного предела первое слагаемое равно 1, а показатель степени и второе слагаемое взаимно обратные. Эти обязательные условия следует учитывать и сначала преобразовывать функцию к виду (9.2), а потом проводить вычисления.
Пример 9.6. Вычислить пределы функций.
1) 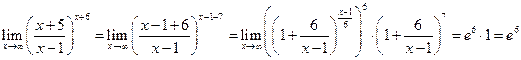 .
.
2)  .
.
3)  , т.к.
, т.к. 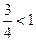 .
.
4)  , т.к.
, т.к.  .
.
9.10. Начисление непрерывных процентов
Пусть к началу года в нашем распоряжении имеется сумма Q0 рублей. Как добиться к концу года максимального роста этой суммы? Один из способов – воспользоваться услугами банка. Предположим, что банк дает 100% годовых; это означает, что за год хранения вклад возрастет на 100%. За любой меньший срок вклад возрастает пропорционально этому сроку (например, за один месяц прирост составит 100/12 процентов).
Итак, после года хранения, вклад станет 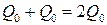 , т.е. удвоится. Можно, однако, добиться большего эффекта, если по истечении полугода закрыть счет и тут же открыть его снова на очередные полгода. В этом случае к концу первого полугода вклад станет равным
, т.е. удвоится. Можно, однако, добиться большего эффекта, если по истечении полугода закрыть счет и тут же открыть его снова на очередные полгода. В этом случае к концу первого полугода вклад станет равным 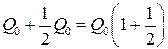 , а к концу года будет равным
, а к концу года будет равным 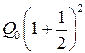 . Вспомните как мы исчисляли проценты в первой лекции!
. Вспомните как мы исчисляли проценты в первой лекции!
Если операцию по закрытию и открытию счета производить чаще, то получим еще больший эффект: например, если эту операцию проводить в конце каждого месяца, то к концу года будем иметь 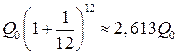 , а если закрывать и открывать счет каждый день, то конечная сумма составит
, а если закрывать и открывать счет каждый день, то конечная сумма составит
 .
.
Если представить себе (что, конечно, является абстракцией), что операция закрытия-открытия производится непрерывно, то в итоге к концу года вклад составит
 руб.
руб.
Таким образом, при номинальной ставке 100% эффективная ставка может составить 172%, что существенно лучше.
Аналогично рассуждения можно провести для случая, когда номинальная ставка будет p% (вмест0 100%). Тогда (теоретически) возможная конечная ставка вклада будет
 .
.
Если вклад хранится не один год, а любое количество t лет, то получим формулу
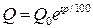 ,
,
которая называется формулой непрерывных процентов.
Замечание. Хотя в практических финансово-кредитных операциях непрерывное исчисление процентов не применяется, оно оказывается весьма эффективным при анализе сложных финансовых проблем, в частности при объективном выборе инвестиционных решений.
Лекция 10.
НЕПРЕРЫВНОСТЬ ФУНКЦИИ
ПЛАН 1. Введение. 2. Определение непрерывности функции.Лекция 11.
ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
ПЛАН 1. ВведениеРис. 11.1
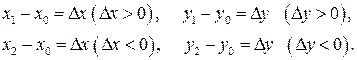
Приращения аргумента  могут быть разных знаков – в первом случае положительное, во втором – отрицательное. И связанные с ними приращения функции
могут быть разных знаков – в первом случае положительное, во втором – отрицательное. И связанные с ними приращения функции 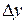 также могут быть иметь разные знаки. Главное, внимательно смотреть и учитывать эту разницу, что поможет в дальнейшем при исследовании функции.
также могут быть иметь разные знаки. Главное, внимательно смотреть и учитывать эту разницу, что поможет в дальнейшем при исследовании функции.
Если функция задана таблично, то ее приращения находят как разности значений, стоящих в соседних клетках. Их величины вписывают в отдельную строку в левое, правое или промежуточное положение.
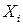 /квартал /квартал
| I | II | III | IV |
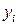 прибыль, млн. руб. прибыль, млн. руб.
| ||||
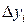 цепной прирост, цепной прирост,
| +30 | -40 | +30 |
В экономике эти разности 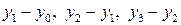 и т.д. называют абсолютным или цепным приростом. В математике – конечными разностями первого порядка. Разности для аргумента
и т.д. называют абсолютным или цепным приростом. В математике – конечными разностями первого порядка. Разности для аргумента  всюду одинаковые и равны, в нашем случае, 1 кварталу (а могут быть равными 1 мес., 1 год и т. д. – то есть шагу таблицы).
всюду одинаковые и равны, в нашем случае, 1 кварталу (а могут быть равными 1 мес., 1 год и т. д. – то есть шагу таблицы).
11.4. Задачи, приводящие к понятию производной
 Рассмотрим кусочек мела, лежащий на столе. Подкинем его вверх с некоторой начальной скоростью, и он за некоторое время
Рассмотрим кусочек мела, лежащий на столе. Подкинем его вверх с некоторой начальной скоростью, и он за некоторое время 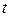 поднимется на высоту
поднимется на высоту 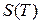 . Его скорость в каждый момент движения будет разной (рис.11.2). Как ее найти? И вот тут вступает в силу древний как мир совет королям: «Разделяй и властвуй». Он «работает» и в математике, особенно в дифференциальном и интегральном исчислении.
. Его скорость в каждый момент движения будет разной (рис.11.2). Как ее найти? И вот тут вступает в силу древний как мир совет королям: «Разделяй и властвуй». Он «работает» и в математике, особенно в дифференциальном и интегральном исчислении.
Поскольку нас интересует скорость в каждый момент времени (и, следовательно, в каждой точке пространства), то логично разбить весь временной интервал Т, за который мел летит вверх, на 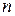 равных частей
равных частей 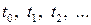 ,
, 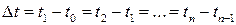 .
.
Пусть к моменту времени 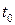 мел был на высоте
мел был на высоте 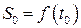 . В момент времени
. В момент времени 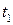
 . Скорость на участке времени от
. Скорость на участке времени от 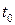 до
до 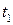 определяется отношением
определяется отношением
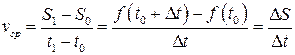 .
.
Так как тело движется вверх и на него действует сила тяжести, то скорость в точках 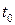 и
и 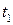 будет отличаться друг от друга. Это различие можно уловить, если
будет отличаться друг от друга. Это различие можно уловить, если 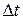 устремить к нулю. А как было показано в лекции 9 – если кто-то куда-то стремиться – нужно вычислять предел. Поэтому мгновенная скорость равна пределу отношения приращения пути к вызвавшему его приращению времени, при стремлении последнего к нулю, т.е.
устремить к нулю. А как было показано в лекции 9 – если кто-то куда-то стремиться – нужно вычислять предел. Поэтому мгновенная скорость равна пределу отношения приращения пути к вызвавшему его приращению времени, при стремлении последнего к нулю, т.е.
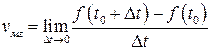 .
.
Вычисление пределов подобного рода – не единичная задача. Рассмотрим тонкий прямолинейный неоднородный стержень длиной l (рис. 11.3). Определим плотность стержня в каждой его точке. Положим его на ось 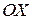 , тогда каждая точка будет иметь свою координату
, тогда каждая точка будет иметь свою координату 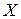 .
.
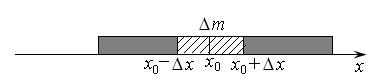
Рис. 11.3
Обозначим через 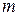 массу отрезка стержня. В силу неоднородности стержня его масса будет зависеть от координаты
массу отрезка стержня. В силу неоднородности стержня его масса будет зависеть от координаты 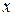 , т.е.
, т.е. 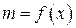 . Рассмотрим некоторую фиксированную точку
. Рассмотрим некоторую фиксированную точку 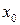 и переменную точку
и переменную точку  . Если положить, что длина стержня равна его массе
. Если положить, что длина стержня равна его массе 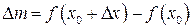 , то его средняя плотность
, то его средняя плотность 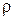 определится как отношение
определится как отношение
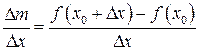 .
.
При стремлении к нулю  получим плотность стержня в точке
получим плотность стержня в точке 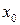 , т.е.
, т.е.
 .
.
Третий пример относится к производственной задаче с определением производительности труда в разные моменты рабочей смены при конвейерной сборке автомобилей. Первыми ее решали американцы. Для того, чтобы снизить затраты на электроэнергию, и на конвейере не было простоев и «запарок,» были проведены энергометрические исследования. В утренние часы в начале смены производительность труда – отношение числа сделанных операций к единице времени, была низкой, потом повышалась, к обеду вновь уменьшалась, т.е. зависела от времени:
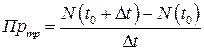 ,
,
где  – количество произведенных операций,
– количество произведенных операций, 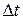 – отрезок времени. В соответствии с проведенными исследованиями был установлен скоростной режим для ленты транспортера, управляемый компьютером. В каждый момент времени он учитывал физические способности человека и двигался так, чтобы процесс производства протекал наименее утомительно и эффективно.
– отрезок времени. В соответствии с проведенными исследованиями был установлен скоростной режим для ленты транспортера, управляемый компьютером. В каждый момент времени он учитывал физические способности человека и двигался так, чтобы процесс производства протекал наименее утомительно и эффективно.
Как и в первых двух примерах, производительность труда в данный момент времени (и скорость ленты транспортера), определяется через знакомый предел
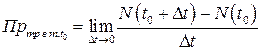 .
.
11.5. Производная функции, заданной аналитически
Отвлечемся от конкретных задач. Пусть дана функция 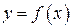 , определенная в точке
, определенная в точке 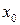 . Дадим приращение аргументу
. Дадим приращение аргументу  , тогда функция получит приращение
, тогда функция получит приращение 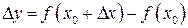 .
.
Определение 11.1. Производной функции 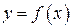 в точке
в точке 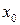 называется предел отношения приращения функции
называется предел отношения приращения функции 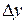 к вызвавшему его приращению аргумента
к вызвавшему его приращению аргумента  при стремлении
при стремлении  к нулю произвольным образом.
к нулю произвольным образом.
Итак,
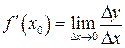 ,
,
или
 .
.
Термин «производная» – «derivative» (англ.) – «die ableutung» (нем.) означает «выведенное из функции, добытое, произведенное по определенному правилу» – как предел отношений бесконечно малых приращений.
Для одной и той же функции производную можно вычислить в различных точках. Множество значений  будет также являться функцией от аргумента
будет также являться функцией от аргумента 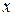 . Эту новую функцию обозначают символами
. Эту новую функцию обозначают символами  и называют производной функции
и называют производной функции 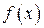 . Тогда
. Тогда 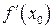 – ее частное значение в точке
– ее частное значение в точке 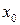 .
.
Операция нахождения производной называется дифференцированием функции. Она проводится по правилу, описанному в определении производной.
Пример 11.2. Найти производную функции  в общем виде и в точке
в общем виде и в точке 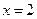 .
.
Решение. Пусть x – любая точка. Дадим приращение аргументу  . Тогда функция получит приращение
. Тогда функция получит приращение 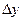 , равное разности между новым и старым значениями функции:
, равное разности между новым и старым значениями функции:
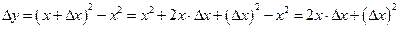 .
.
Найдем
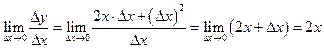 .
.
Таким образом,  . В точке
. В точке  .
.
11.6. Таблица производных
Естественно, что все элементарные функции были продифференцированы еще в 18 веке, и мы пользуемся готовыми формулами, которые сведены в таблицу. Советуем выучить ее наизусть, как таблицу умножения, потому что это тот язык, на котором говорит высшая математика.
Посмотрите внимательно на эти формулы. Некоторые из них вам знакомы из школы, остальные вы видите впервые. Какой вывод можно сделать? – Производная отличается от своей первообразной функции почти всегда: дифференцирование приводит не только к изменению показателя степени для 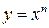 , но и к изменению вида аналитического выражения:
, но и к изменению вида аналитического выражения: 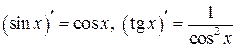 . И только одна функция осталась неизменной: это
. И только одна функция осталась неизменной: это 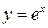 , которую назвали экспонентой. Позднее мы увидим, что и
, которую назвали экспонентой. Позднее мы увидим, что и  . Число
. Число  – это число Эйлера, с которым мы познакомились во втором замечательном пределе.
– это число Эйлера, с которым мы познакомились во втором замечательном пределе.
Таблица производных простейших элементарных функций
1.  , ,
| 5. 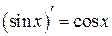 , ,
|
2.  , ,
| 6. 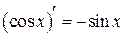 , ,
|
2а.  , ,
| 7. 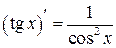 , ,
|
2б.  , ,
| 8.  , ,
|
2в.  , ,
| 9. 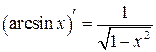 , ,
|
3.  , ,
| 9а.  , ,
|
3а.  , ,
| 10.  , ,
|
4.  , ,
| 10а. 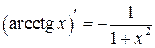 . .
|
4а. 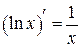 , ,
|
Вопрос: любую ли функцию можно продифференцировать, во всех ли точках функция может иметь производную? На него ответит следующий пункт.
11.7. Связь между непрерывностью и дифференцируемостью функции
В лекции 10 «Непрерывность функции» мы дали следующее определение непрерывности функции в точке 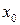 :
:
Функция 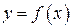 непрерывна в точке
непрерывна в точке 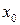 , если бесконечно малому приращению аргумента
, если бесконечно малому приращению аргумента  соответствует бесконечно малое приращение функции
соответствует бесконечно малое приращение функции 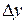 . То есть для непрерывности функции надо, чтобы приращение
. То есть для непрерывности функции надо, чтобы приращение  и
и 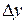 были сравнимы или одного порядка малости.
были сравнимы или одного порядка малости.
Но те же самые 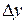 и
и  присутствуют в производной:
присутствуют в производной: 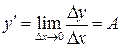 , где
, где 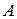 – скорость процесса в рассматриваемой точке. Если известно, что производная в данной точке существует, то отсюда следует, что
– скорость процесса в рассматриваемой точке. Если известно, что производная в данной точке существует, то отсюда следует, что 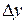 и
и  – б.м.в. одного порядка малости и, следовательно
– б.м.в. одного порядка малости и, следовательно  – непрерывна в данной точке.
– непрерывна в данной точке.
Если функция  дифференцируема в точке
дифференцируема в точке 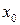 , то она непрерывна в этой точке.
, то она непрерывна в этой точке.
Будет ли верна обратная теорема? Если функция непрерывна в точке 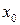 ,будет ли она в ней иметь производную? Не спешите давать утвердительный ответ.
,будет ли она в ней иметь производную? Не спешите давать утвердительный ответ.
Мы должны сказать, что в математике кроме прямых доказательств какого-либо утверждения можно приводить контр-примеры, которые показывают, что данное утверждение ошибочно. И тогда теорема отвергается или принимается с оговорками типа «за исключением некоторых точек». Этой фразой нас предупреждают о подводных камнях.
Итак, контрпример. Функция 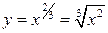 непрерывна для всех
непрерывна для всех 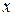 . По формуле 2 из таблицы производных найдем ее производную:
. По формуле 2 из таблицы производных найдем ее производную: 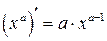 ; у нас
; у нас 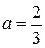 ,
, 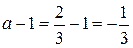 и
и 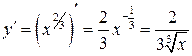 . Эта функция определена для всех
. Эта функция определена для всех 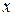 , кроме нуля. То есть несмотря на то, что исходная функция непрерывна, ее производная имеет разрыв в точке
, кроме нуля. То есть несмотря на то, что исходная функция непрерывна, ее производная имеет разрыв в точке 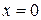 , да еще II рода (бесконечный). График данной функции
, да еще II рода (бесконечный). График данной функции 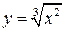 приведен на рисунке 11.4а.
приведен на рисунке 11.4а.
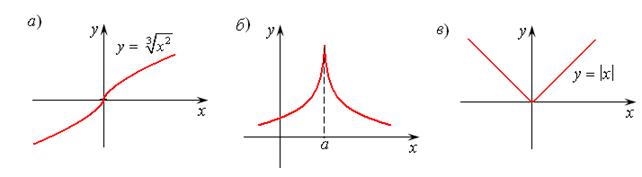
Рис. 11.4
Аналогично функция (рис. 11.4б) будет иметь разрыв производной в точке 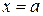 . На рис. 11.4в приведен график функции
. На рис. 11.4в приведен график функции 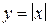 , которая непрерывна для всех
, которая непрерывна для всех 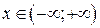 . Так как
. Так как
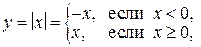 то
то 
То есть производная в точке 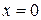 слева равна –1, а справа +1. Но по определению производная не зависит от способа стремления к данной точке,
слева равна –1, а справа +1. Но по определению производная не зависит от способа стремления к данной точке,  произвольно и как слева, так и справа от нуля должно получиться одно число, а у нас – разные. Поэтому производной функции
произвольно и как слева, так и справа от нуля должно получиться одно число, а у нас – разные. Поэтому производной функции  в точке
в точке 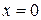 не существует.
не существует.
Поэтому говорят, что функции 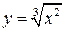 ,
, 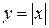 и т. д. непрерывны на интервале
и т. д. непрерывны на интервале  , а дифференцируемы на объединении полуинтервалов
, а дифференцируемы на объединении полуинтервалов  , т.е. всюду, кроме точки
, т.е. всюду, кроме точки 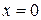 (или любой другой точки).
(или любой другой точки).
Данные примеры показывают, что связь между дифференцированием и непрерывностью односторонняя: из первого следует второе, но из второго первое не всегда, поэтому требование дифференцируемости более жесткое, чем требование непрерывности.
11.8. Геометрический смысл производной.
Графическое дифференцирование
Для того, чтобы усвоение многих понятий математического анализа было легче и зрительно понятнее, рассмотрим второй подход к описанию производной – геометрический, который открыл великий немец Готфрид Вильгельм Лейбниц.
 Но прежде договоримся о терминологии. Что такое касательная? Самый простой ответ – эта прямая, имеющая одну общую точку с кривой. Ответ неправильный, контрпример: ось параболы пересекается с ней в одной точке, но это не касательная (рис. 11.5).
Но прежде договоримся о терминологии. Что такое касательная? Самый простой ответ – эта прямая, имеющая одну общую точку с кривой. Ответ неправильный, контрпример: ось параболы пересекается с ней в одной точке, но это не касательная (рис. 11.5).
Дадим строгое определение касательной к кривой в данной точке.
Рассмотрим плоскую кривую  . Проведем секущую
. Проведем секущую  . Если точка
. Если точка 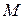 начнет перемещаться к точке
начнет перемещаться к точке 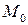 , остающейся неподвижной, то секущая
, остающейся неподвижной, то секущая  начнет менять свое положение, все более приближаясь к некоторой прямой
начнет менять свое положение, все более приближаясь к некоторой прямой 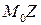 называется касательной (рис. 11.6).
называется касательной (рис. 11.6).
Рис. 11.6 Рис. 11.7
Определение 11.2.Касательная есть прямая, занимающая предельное положение секущей.
Аналогично вводится касательная и к пространственной кривой.
Вернемся к производной. Рассмотрим график функции 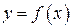 , имеющий в точке
, имеющий в точке 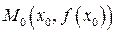 невертикальную касательную (рис. 11.7). Проведем ее до пересечения с осью
невертикальную касательную (рис. 11.7). Проведем ее до пересечения с осью 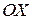 – это будет угол
– это будет угол 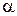 . Угловой коэффициент
. Угловой коэффициент 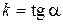 .
.
Теперь рассмотрим секущую  , где точка
, где точка 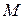 имеет координаты
имеет координаты  . Угол, который она составляет с осью
. Угол, который она составляет с осью 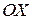 , равен b, и
, равен b, и
 . (11.6)
. (11.6)
Если  , то
, то 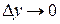 в силу непрерывности функции, и точка
в силу непрерывности функции, и точка 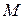 устремится к точке
устремится к точке 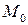 . Секущая
. Секущая  неограниченно приближается к положению касательной
неограниченно приближается к положению касательной  и
и 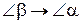 , следовательно
, следовательно 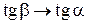 или в форме пределов
или в форме пределов
 . (11.7)
. (11.7)
Но 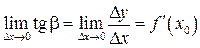 по определению.
по определению.
Таким образом,угловой коэффициент касательной к графику функции в точке  равен значению производной в этой точке
равен значению производной в этой точке
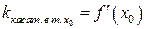 . (11.8)
. (11.8)
Иногда уточняют и говорят, что тангенс угла наклона касательной равен производной функции в этой точке.
Касательную можно проводить к любой гладкой, т.е. не имеющей «изломов», кривой (см. рис. 11.4в). В точках изломов касательную провести невозможно (рис. 11.4а, б).
А теперь покажем, как можно построить график производной функции 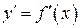 , если известен график исходной функцией
, если известен график исходной функцией 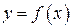 . Эта операция называется графическим дифференцированием.
. Эта операция называется графическим дифференцированием.
Пусть график функции 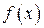 приведен на рис. 11.8. Разобьем отрезок
приведен на рис. 11.8. Разобьем отрезок 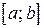 , на котором определена
, на котором определена 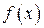 на
на 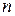 частей с помощью точек
частей с помощью точек  . На данном графике им будут соответствовать точки
. На данном графике им будут соответствовать точки 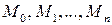 . Через каждую точку проведем касательные. Через точку
. Через каждую точку проведем касательные. Через точку 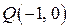 проведем параллельные этим касательным прямые
проведем параллельные этим касательным прямые 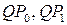 и т.д. до их пересечения с осью
и т.д. до их пересечения с осью 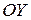 . Отрезки
. Отрезки 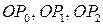 и т.д. равны значениям производной
и т.д. равны значениям производной 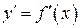 соответственно в точках
соответственно в точках  и т.д. Действительно, например, в треугольнике
и т.д. Действительно, например, в треугольнике  , т.к.
, т.к. 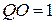 . Но согласно геометрическому смыслу
. Но согласно геометрическому смыслу  , поэтому
, поэтому  . Как получаются точки
. Как получаются точки 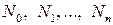 понятно из чертежа. Они имеют координаты
понятно из чертежа. Они имеют координаты 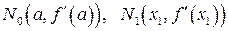 , …,
, …, 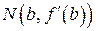 . Соединив эти точки плавной кривой, получим приближенный график производной
. Соединив эти точки плавной кривой, получим приближенный график производной 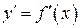 , по которому нетрудно найти приближенное значение этой производной в любой точке отрезка
, по которому нетрудно найти приближенное значение этой производной в любой точке отрезка 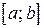 . Ясно, что построение графика производной тем точнее, чем большее число точек деления
. Ясно, что построение графика производной тем точнее, чем большее число точек деления 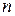 . Значения производной найдутся тем точнее, чем точнее определится длина отрезков
. Значения производной найдутся тем точнее, чем точнее определится длина отрезков  .
.
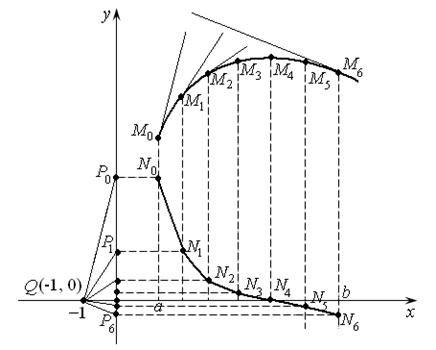
Рис. 11.8
Графическое дифференцирование является хорошим подспорьем, а иногда и единственной возможностью для определения скорости изменения процесса, описанного графиком.
 Пример 11.4. На графике функции
Пример 11.4. На графике функции  найти точку, в которой касательная составляет угол
найти точку, в которой касательная составляет угол  с осью OX. Сделать чертеж.
с осью OX. Сделать чертеж.
Решение. Сделаем рисунок (см. рис. 11.9).
Воспользуемся формулой  в точке x0.
в точке x0.
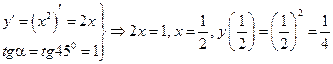 .
.
Таким образом, в точке  касательная будет направлена под углом
касательная будет направлена под углом  к положительному направлению оси OX.
к положительному направлению оси OX.
Пример 11.5. Из всех показательных функций выбрать ту, у которой производная в точке  равна единице.
равна единице.
Решение. В таблице производных найдем 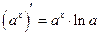 при любом
при любом 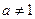 . В точке
. В точке  И
И 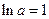 только в том случае, если
только в том случае, если 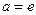 . То есть из всех показательных функций только при
. То есть из всех показательных функций только при  производная
производная 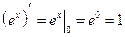 имеет касательную с углом наклона
имеет касательную с углом наклона  к положительному направлению оси OX.
к положительному направлению оси OX.
11.9. Производная функции, заданной таблично
Прежде чем рассматривать этот пункт, вспомним еще раз определение производной.
Производная функции – это предел отношения приращения функции 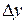 к вызвавшему его приращению аргумента
к вызвавшему его приращению аргумента  при стремлении
при стремлении  к нулю произвольным образом.
к нулю произвольным образом.
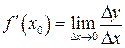 , или
, или  .
.
Оговоримся сразу, что никакая таблица, даже с очень малым шагом 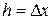 , не может выполнить требование
, не может выполнить требование  . Да в этом часто нет необходимости, особенно если рассматривать экономические процессы, протекающие в длительные временные периоды. Поэтому под табличной производной понимают отношение приращения
. Да в этом часто нет необходимости, особенно если рассматривать экономические процессы, протекающие в длительные временные периоды. Поэтому под табличной производной понимают отношение приращения 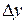 (строка 4 таблицы 11.2) к приращению
(строка 4 таблицы 11.2) к приращению  .
.  , где
, где  – шаг таблицы или
– шаг таблицы или 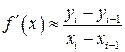 . Неточность будет тем выше, чем больше значение
. Неточность будет тем выше, чем больше значение  или
или 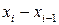 . Эта производная характеризует скорость протекания процесса за данный период времени. Если цифры таблицы нанести на график, и соединить рядом стоящие точки отрезками прямых
. Эта производная характеризует скорость протекания процесса за данный период времени. Если цифры таблицы нанести на график, и соединить рядом стоящие точки отрезками прямых 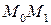 ,
,  (рис. 11.10), то скорости будут пропорциональны тангенсам углов наклона этих отрезков к оси
(рис. 11.10), то скорости будут пропорциональны тангенсам углов наклона этих отрезков к оси 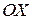 .
.
Таблица 11.2.
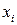 , период , период
| январь | февраль | март | апрель | май | июнь |
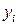 , объем производства, млн. руб. , объем производства, млн. руб.
| ||||||
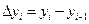
| +5 | +15 | –10 | –30 | +50 | |
 , , 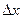 – 1 мес. – 1 мес.
| –10 | –30 |

Рис. 11.10
В данной таблице нас будет интересовать и значение 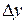 и его знак. Из смысла задачи понятно, что чем больше
и его знак. Из смысла задачи понятно, что чем больше 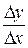 , тем больше скорость возрастания объемов производства в денежном изображении за месяц. В нашем случае наиболее удачным оказался март, убыточным – май.
, тем больше скорость возрастания объемов производства в денежном изображении за месяц. В нашем случае наиболее удачным оказался март, убыточным – май.
Точки 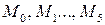 можно соединить плавной прямой и применить метод графического дифференцирования при уверенности, что в промежуточных точках нет изломов.
можно соединить плавной прямой и применить метод графического дифференцирования при уверенности, что в промежуточных точках нет изломов.
Для более строгого определения производной функции, заданной таблицей, вначале рассчитываются интерполяционные формулы Ньютона или Лагранжа, описывающие таблицу с 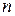 точками в виде многочлена
точками в виде многочлена 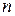 -ой степени, а уже потом для полученного многочлена находят производную Эти задачи решаются на ЭВМ и не входят в рассмотрение данного курса. Их можно найти в литературе.
-ой степени, а уже потом для полученного многочлена находят производную Эти задачи решаются на ЭВМ и не входят в рассмотрение данного курса. Их можно найти в литературе.
Вообще величина 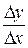 бывает очень полезной для экономистов, потому что в общем случае она показывает во сколько раз приращение
бывает очень полезной для экономистов, потому что в общем случае она показывает во сколько раз приращение 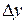 больше (или меньше) приращения
больше (или меньше) приращения  , например, отношение прибыли от каких – либо мероприятий к затратам на эти мероприятия. Позднее мы рассмотрим такую задачу, а пока закончим лекцию еще одним понятием, тесно связанным с приращением функции. Это новое понятие – дифференциал.
, например, отношение прибыли от каких – либо мероприятий к затратам на эти мероприятия. Позднее мы рассмотрим такую задачу, а пока закончим лекцию еще одним понятием, тесно связанным с приращением функции. Это новое понятие – дифференциал.
11.10. Дифференциал функции. Приложение к
приближенным вычислениям.
 Рассмотрим функцию
Рассмотрим функцию 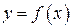 , непрерывную и дифференцируемую на отрезке
, непрерывную и дифференцируемую на отрезке 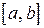 . Ее график представлен на рис. 11.11. Возьмем произвольную точку
. Ее график представлен на рис. 11.11. Возьмем произвольную точку 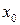 . Отрезок
. Отрезок  равен сумме двух отрезков
равен сумме двух отрезков 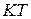 и
и  , причем
, причем 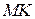 - это приращение всей функции, а
- это приращение всей функции, а  это приращение касательной M0T. Из
это приращение касательной M0T. Из 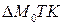

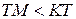 , если
, если  .
.
Величина 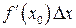 , представляющая главную часть приращения
, представляющая главную часть приращения 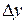 , линейная относительно
, линейная относительно  , называется дифференциалом функциии обозначается
, называется дифференциалом функциии обозначается  , то есть
, то есть
.
Тогда
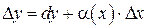 , (11.9)
, (11.9)
где  – величина более высокого порядка малости, чем
– величина более высокого порядка малости, чем  .
.
Если положить 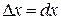 , т. е. считать, что дифференциал независимой переменной
, т. е. считать, что дифференциал независимой переменной  равен ее приращению, то выражение для дифференциала функции запишется в следующей форме:
равен ее приращению, то выражение для дифференциала функции запишется в следующей форме:
 , или
, или 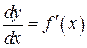 . (11.10)
. (11.10)
Таким образом,производная функции равна отношению ее дифференциала  к дифференциалу независимой переменной
к дифференциалу независимой переменной .
.
Часто отношение дифференциалов рассматривается как символ производной. Именно так его изобразил Лейбниц.
Более детальное рассмотрение темы «Дифференциал» можно найти в рекомендуемой литературе. Укажем лишь практическое применение дифференциала для приближенных вычислений. Воспользуемся формулой (11.9). Отбросим бесконечно малую величину  , тогда получим
, тогда получим
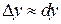 . (11.11)
. (11.11)
Так как 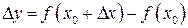 и
и  , то
, то
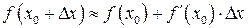 . (11.12)
. (11.12)
Эту формулу используют для приближенного вычисления.
Пример 11.3. Оценить значение 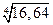 .
.
Решение. Полагая 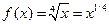 , найдем
, найдем
 .
.
Тогда
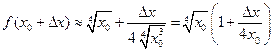 .
.
В качестве x0 возьмем число, близкое к 16,64, но чтобы был известен 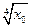 , при этом Dx должен быть достаточно мал. Очевидно, что следует взять
, при этом Dx должен быть достаточно мал. Очевидно, что следует взять 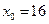 и
и 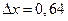 (но, например, не
(но, например, не  и
и 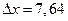 ). Анализ показывает, что точность формулы (11.12) зависит от
). Анализ показывает, что точность формулы (11.12) зависит от 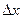 : чем больше
: чем больше 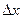 , тем ниже точность. Итак,
, тем ниже точность. Итак,
 .
.
Отметим, что формула (11.12) обычно используется для достаточно грубых оценок, более точные результаты можно получить при помощи степенных рядов, о которых можно прочитать в приведенной литературе.
В настоящее время подобные расчеты никто делать не будет, если под рукой имеется хороший калькулятор, позволяющий вычислять корни любых степеней. В нашем случае калькулятор выдает следующий результат:

Более актуальной является задача об оценке приближенных вычислений. Это связано с тем, что мы, как правило, имеет дело только данными, значения которых известны с некоторой погрешностью. Используя эти данные, мы вычисляем какие-либо показатели или характеристики, но они тоже будут вычислены с некоторой погрешностью. Какой? Вот здесь нам и пригодится формула (11.11). Проиллюстрируем это на простом примере.
Пример 11.4. Пусть имеется квадратный участок со стороной 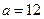 м. Абсолютная погрешность измерения стороны квадрата составила
м. Абсолютная погрешность измерения стороны квадрата составила 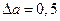 м. Какова абсолютная погрешность вычисления площади участка?
м. Какова абсолютная погрешность вычисления площади участка?
Решение. Вы помните, что площадь квадрата равна
 м2.
м2.
Для оценки погрешности вычислений воспользуемся формулой (11.11):
 м2.
м2.
Ответ запишем следующим образом:
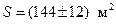 .
.
11.11. Заключение
Итак, сделаем первые выводы по определению производной:
1. Производная функции 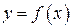 – это новая функция
– это новая функция 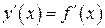 , вычисленная по особым правилам
, вычисленная по особым правилам  .
.
2. Производная применяется для физической и геометрической характеристики изменения функции: с одной стороны она указывает на скорость, а с другой – на угол наклона касательной: чем больше скорость и тангенс угла наклона – тем сильнее будет изменяться функция.
3. С понятием производной тесно связано понятие дифференциала функции  , как главной части приращения, линейного относительно,
, как главной части приращения, линейного относительно, 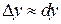 , где
, где 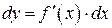 , откуда
, откуда 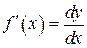 .
.
Для того чтобы найти производную – нужно найти предел отношения приращения дифференциалов 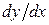 . Для того, чтобы найти дифференциал – нужно найти производную и умножить ее на дифференциал независимой переменной
. Для того, чтобы найти дифференциал – нужно найти производную и умножить ее на дифференциал независимой переменной  .
.
Дифференциалы используются для приближенных вычислений по формуле: 
4. Что нового вы еще узнали?
На следующей лекции перейдем непосредственно к технике дифференцирования и взятия производной.
Лекция 12.
ТЕХНИКА ДИФФЕРЕНЦИРОВАНИЯ РАЗЛИЧНЫХ ФУНКЦИЙ. ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ
ПЛАН 1. Правила дифференцирования арифметических действий. 2. Производная сложной функции.Таблица правил дифференцирования основных арифметических действий.
| Производная | Дифференциал |
1. 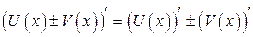 , ,
| 1.  , ,
|
2. 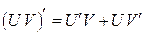 , ,
| 2.  , ,
|
2а.  , где , где  , ,
| 2а.  , где , где  , ,
|
2б.  , ,
| 2б. 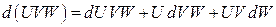 , ,
|
3.  , ,
| 3. 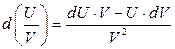 . .
|
Докажем формулу 3, как наименее очевидную. Следуем строго по определению производной:
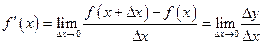 .
.
Пусть  и
и  дифференцируемы в точке х. Дадим
дифференцируемы в точке х. Дадим 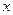 приращение
приращение 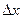 , тогда функции тоже получат приращение
, тогда функции тоже получат приращение
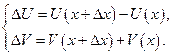
Для частного 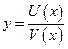 общее приращение найдется из соотношения
общее приращение найдется из соотношения
 .
.
Составим отношение  и перейдем к пределу при
и перейдем к пределу при  :
:
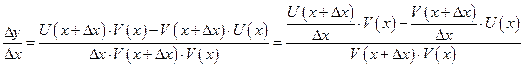 ,
,
 .
.
Для дальнейших вычислений в числителе этой дроби добавим и отнимем выражение 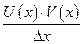 . Дробь при этом не изменится
. Дробь при этом не изменится

что и требовалось доказать.
При вычислении производных, особенно на первых этапах, следует сначала выделять главное действие и к нему подбирать правило, а потом применять соответствующие формулы из таблицы производных.
Пример 12.1. Вычислить производные следующих функций:
а) 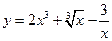 .
.
Здесь главное действие – сумма, поэтому
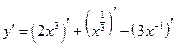 .
.
Постоянные вынесем за знаки производных, к каждому слагаемому применим формулу 2 из таблицы производных, получим:
 .
.
б)  .
.
Здесь тоже главное действие сумма, но второе слагаемое представляет собой частное, а третье – произведение. Учтя эти обстоятельства, имеем:
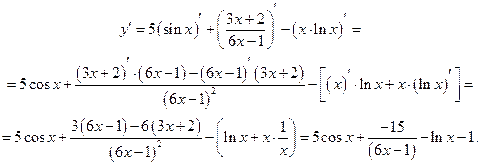
в)  .
.
Здесь главное действие – частное, у которого в числителе разность произведений. Аккуратно следуем за правилами.
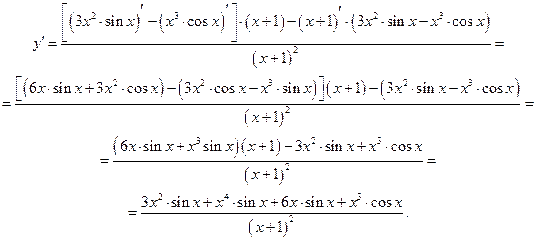
г)  .
.
Воспользуемся формулой 2б (тройное произведение), причем последний множитель – дробь.
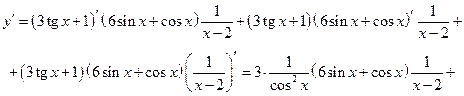

Пример 12.2. Вычислить дифференциалы функций.
а)  – сумма, у которой последнее слагаемое – произведение. Для удобства последующих вычислений вспомним, что
– сумма, у которой последнее слагаемое – произведение. Для удобства последующих вычислений вспомним, что  и будем сразу вычислять производные, поставив сомножитель
и будем сразу вычислять производные, поставив сомножитель  в конце выражения. Вот так:
в конце выражения. Вот так:
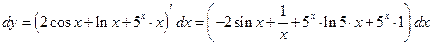 .
.
б) 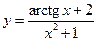
Находим
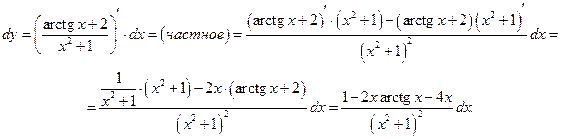
На какие выводы наталкивают рассмотренные примеры?
1. Нужно правильно выделять главное действие;
2. нужно хорошо знать таблицы правил и формул дифференцирования;
3. четко следовать всем инструкциям.
И тогда самые трудные примеры будут решаться просто. Но жизнь – штука сложная, поэтому перейдем к технике дифференцирования сложных, неявных и степенно-показательных функций.
12.2. Производная сложной функции
Определение 12.3. Величина  называется функцией от функции (или сложной функцией), если она является функцией от вспомогательной переменной
называется функцией от функции (или сложной функцией), если она является функцией от вспомогательной переменной  , которая в свою очередь зависит от переменной
, которая в свою очередь зависит от переменной 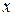 , то есть
, то есть  ,
,  , тогда
, тогда 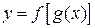 .
.
Например:  , здесь
, здесь  – промежуточный аргумент.
– промежуточный аргумент.
Часто промежуточных аргументов бывает несколько, поэтому перед взятием производной следует хорошо представить себе все промежуточные функции и их аргументы – то есть ясно увидеть цепочку сложности.
Например:  . Рассмотрим всю серию промежуточных аргументов и функций, которые имеет данное выражение. Поскольку все начинается с
. Рассмотрим всю серию промежуточных аргументов и функций, которые имеет данное выражение. Поскольку все начинается с 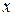 , то цепочку сложности запишем в следующем порядке:
, то цепочку сложности запишем в следующем порядке:
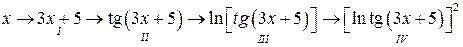 .
.
I звено: функция сумма, аргумент –  ,
,
II звено: функция –  , аргумент –
, аргумент – 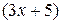 ,
,
III звено: функция –  , аргумент –
, аргумент – 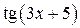 ,
,
IV звено: функция – степень (квадрат), аргумент 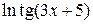 ,
,
то есть то, что раньше было функцией, в последующем звене становиться аргументом.
Если  , то ее цепочка выглядит так:
, то ее цепочка выглядит так:
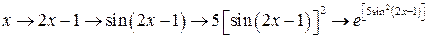 .
.
Умение расписывать эти цепочки становиться особенное актуальным, если учесть следующую теорему о производной сложной функции.
Теорема 12.4. Пусть  и
и  , причем в некоторой точке x существует производная
, причем в некоторой точке x существует производная 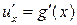 и в соответствующей точке
и в соответствующей точке 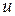
 . Тогда сложная функция
. Тогда сложная функция 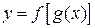 в данной точке
в данной точке 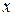 имеет производную
имеет производную  , которая находится по следующей формуле:
, которая находится по следующей формуле:
 , (12.1)
, (12.1)
или в менее точной, но в более короткой формулировке: производная сложной функции равна произведению всех промежуточных функций по промежуточным аргументам, по всем звеньям цепочки сложности.
Доказательство проведем исходя из определения производной на языке приращений.
Дадим 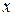 приращение
приращение  . Тогда
. Тогда  и
и  , т. е. u и y получат приращения
, т. е. u и y получат приращения 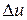 и
и 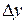 , причем в силу дифференцируемости
, причем в силу дифференцируемости  и
и 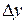 будут сравнимы с
будут сравнимы с  и если
и если  , то и
, то и  ,
, 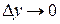 .
.
Запишем очевидное равенство:
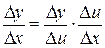 . (12.2)
. (12.2)
Перейдем к пределу при  :
:
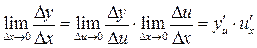 ,
,
где  ,
,  и
и  . Поэтому
. Поэтому  .
.
Что и требовалось доказать.
Понятно, что эта теорема будет верной и для нескольких звеньев промежуточных функций.
Пример 12.3. 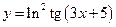 . Найти
. Найти  .
.
Решение. Используем формулу (12.1) этого пункта и разобранную выше цепочку сложности. Имеем:
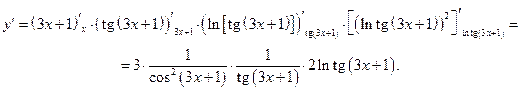
Пример 12.4. Найти производную функции  .
.
Решение.
Окончательный ответ всегда старайтесь максимально упростить, это может очень облегчить жизнь в дальнейшем. При достаточной натренированности нужда в записи цепочки сложности и… Итак, мы разобрали случай, когда функция задана одним, хотя и сложным, выражением.Рис. 12.1
Пример 12.17. Составить уравнение касательной и нормали к графику функции 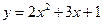 в точке с абсциссой
в точке с абсциссой 
Решение. Найдем значение функции y и ее производную 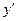 в точке
в точке  :
:
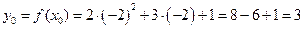 ,
,
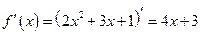 ,
,  .
.
Уравнение касательной: 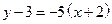 ,
, 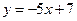 .
.
Уравнение нормали: 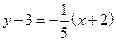 ,
, 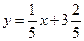 .
.
12.8. Производные и дифференциалы высших порядков
В предыдущих лекциях мы рассмотрели производные многих функций, которые являются в общем случае новыми функциями  , зависящими от аргумента
, зависящими от аргумента 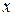 . Поэтому их можно вновь дифференцировать.
. Поэтому их можно вновь дифференцировать.
Определение 12.4. Пусть  есть производная от
есть производная от 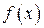 , тогда производная от
, тогда производная от  называется производной второго порядка (или второй производной) от функции
называется производной второго порядка (или второй производной) от функции 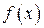 и обозначается
и обозначается 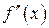 , т. е.
, т. е.
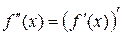 . (12.7)
. (12.7)
Производная от второй производной называется третьей производной или производной третьего порядка и обозначается 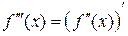 .
.
Аналогично вводятся производные четвертого, пятого и т. д. порядка. Они обозначаются  .
.
Пример 12.18. Найти последовательно все производные от функции 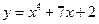 .
.
Решение. 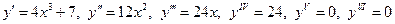 .
.
Понятно, что все правила вычислений производных сложных, неявных и других функций работают в полном объеме и при нахождении производных высших порядков.
Пример 12.19. Найти  функции
функции  .
.
Решение. Найдем  от этой неявной функции.
от этой неявной функции.

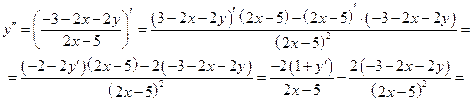
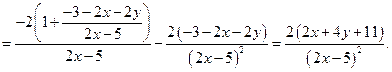
При записи конечного ответа мы вместо 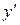 подставили выражение, найденное выше и упростили получившееся выражение.
подставили выражение, найденное выше и упростили получившееся выражение.
Некоторую особенность имеет производная высших порядков функции заданной параметрически.
Пусть
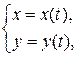
 .
.
Тогда
 . (12.8)
. (12.8)
Иногда для  предпочтительнее другая формула:
предпочтительнее другая формула:
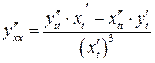 . (12.9)
. (12.9)
Пример 12.20. Найти  , если
, если 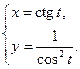
Решение. Воспользуемся формулой (12.8) и найдем сначала 
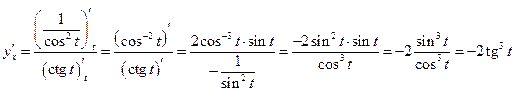 ,
,
 .
.
Пример 12.21. Найти  функции
функции 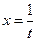 ,
, 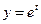 .
.
Решение. Найдем  по формуле 12.9.
по формуле 12.9.
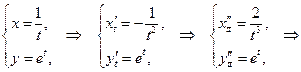
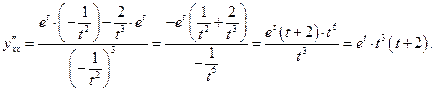
12.9. Дифференциалы высших порядков.
Численное дифференцирование
Поскольку дифференциал (как главная часть приращения функции)  связан с производной
связан с производной 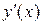 формулой
формулой
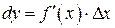 , (12.10)
, (12.10)
где 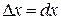 , то естественно ожидать, что и для дифференциалов высших порядков будет выполняться равенство
, то естественно ожидать, что и для дифференциалов высших порядков будет выполняться равенство
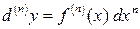 , (12.11)
, (12.11)
где  – дифференциал
– дифференциал  -го порядка функции
-го порядка функции  ,
, 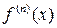 – производная
– производная 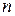 -го порядка этой функции,
-го порядка этой функции, 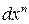 – дифференциал (приращение) независимой переменной
– дифференциал (приращение) независимой переменной 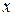 в
в 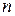 -ой степени.
-ой степени.
Тогда производная  -го порядка в дифференциальной форме запишется так:
-го порядка в дифференциальной форме запишется так:
 . (12.12)
. (12.12)
Если функция задана таблично, то под  понимается разность первого порядка
понимается разность первого порядка
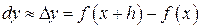 ,
,
где  – шаг таблицы.
– шаг таблицы.
Из разностей первого порядка можно составить разности второго порядка, а из них – третьего и т.д. Их записывают в особые таблицы, которые называются диагональными таблицами разностей.
| 
| 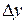
| 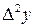
| 
| … |
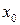
| 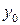
| 
| 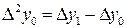
| 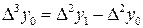
| |

| 
| 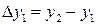
| 
| 
| |
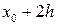
| 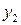
| 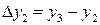
| 
| 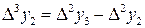
| … |
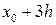
| 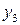
| 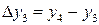
| 
| ||
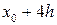
| 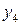
| 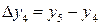
| |||
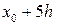
| 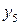
|
В каждой точке 0, 1, 2 … разности имеют свои значения при условии, что  …. В этом случае все
…. В этом случае все  . Они могут быть положительными, отрицательными и равными нулю. Если разность
. Они могут быть положительными, отрицательными и равными нулю. Если разность 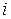 -ого порядка разделить на
-ого порядка разделить на 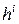 , то получим формулу для вычисления численной производной:
, то получим формулу для вычисления численной производной:
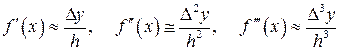 . (12.13)
. (12.13)
Знак приближения связан с тем, что  не стремится к нулю, как это было дано в определении производных. Но чем меньше
не стремится к нулю, как это было дано в определении производных. Но чем меньше  , тем формула точнее.
, тем формула точнее.
Формулы (12.13) – это формулы численного дифференцирования. Более точные (и потому сложные) варианты этих формул можно найти в рекомендуемой литературе. Запомним эти формулы, так как они пригодятся нам в дальнейшем – в экономико-математическом анализе.
Если первая производная кинетически означает скорость любого процесса, то производная второго порядка – ускорение. По аналогии третью производную можно назвать «скорость ускорения», а четвертую – «ускорение ускорения» и т.д.
12.10. Заключение
Остановимся на этом моменте, передохнем. Мы поднялись на такую высоту, на которой даже великие математики 17-18 веков чувствовали себя неуверенно. Они были первыми и искали путь к этой вершине наощупь, с великими догадками и отчаянным непониманием того, что нам теперь кажется хоть и трудоемким, но простым. Оглянемся на пройденный в этой главе путь, сделаем общие выводы. Итак:
1. Производные различных порядков – это новые функции, полученные из исходной по правилу отношения приращений: 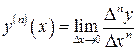
2. Для различных функций – элементарных, сложных, неявных, параметрических – существует своя техника вычислений производной, в основе которых лежит правило дифференцирования сложной функции – правило цепочки. Все действия строго регламентированы правилами и формулами.
3. По большому счету тема «Производная» учит четко выполнять инструкции, данные в особой математической форме, т.е. исполнительской дисциплине, что для экономиста никогда не бывает лишним.
– Конец работы –
Используемые теги: Лекция, Понятие, Функции0.035
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Лекция 8. ПОНЯТИЕ ФУНКЦИИ
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов