ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ

 

ПЛАН

1. Введение.

2. Функция двух переменных. Способы задания. Область определения.

3. Приращения функции: частное и полное.

4. Непрерывность.

5. Частные производные первого порядка

6. Дифференциал

7. Заключение.

 

16.1. Введение

Очень немногие процессы зависят от одной переменной. Жизнь многогранна и зависит от многих факторов. Например, площадь прямоугольника S является функцией его ширины x и длины y, объем параллелограмма V – ширины x, длины y и высоты z и т.д. В первом случае мы имеем дело с функцией двух переменных, во втором – трех переменных. Нетрудно привести примеры, когда в определяющее число факторов будут входить четыре и большее число переменных. Функцию одной переменной мы изучили достаточно полно, перейдем теперь к функции двух переменных.

16.2. Функция двух переменных. Способы задания.
Область определения

Определение 16.1. Если каждой паре (х, у) значений двух независимых друг от друга переменных величин х и у из некоторой области их изменения D соответствует определенное значение величины z, то говорят, что z является функцией от x и y в области D.

Символически функция двух переменных обозначается так:

.

Как и функция одной переменной она может быть задана аналитически, таблично и графически. Переход от одного способа задания к другому осуществляется по тем же правилам, что и для функции одной переменной.

Пусть функция задана формулой 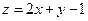. Составим для нее таблицу значений, в первой строке которой будут находиться значения х, а в первом столбце – значения у. Выберем произвольные значения для х и у, а z получается согласно заданному правилу.

x y	0,1	0,2	0,3	0,4
	0,2	0,4	0,6	0,8
	1,2	1,4	1,6	1,8
	2,2	2,4	2,6	2,8
	3,2	3,4	3,6	3,8
	4,2	4,4	4,6	4,8

Для того чтобы построить график этой функции нужно из каждой точки М(х,у) плоскости ХОY поднять перпендикуляр z и потом объединить полученные точки аппликат. Следует учесть, что графическое изображение функции двух переменных в трехмерном декартовом базисе в общем случае представляет некоторую поверхность. В лекции 8 мы показывали, что построение линии «по точкам» страдает приближенностью и даже ошибочностью, потому что не может учесть такие важные точки, как разрывы, экстремумы и т.д. Поэтому если надо построить график поверхности, решают вопрос в общем виде, определив ее тип, а потом переходят к построению.

Если на плоскости самая простая и самая изученная линия – это прямая, то наиболее простая поверхность в пространстве – это плоскость, уравнение которой в общем виде записывается так:

. (16.1)

Разделив обе части равенства на D, получим равносильное уравнение

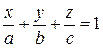, (16.2)

где 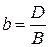, . Его называют уравнением плоскости «в отрезках».

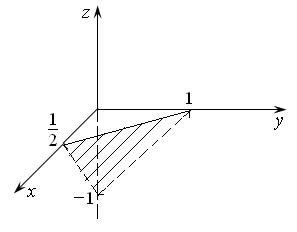
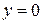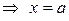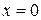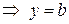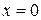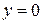
По полученному уравнению (16.2) легко изобразить плоскость в декартовой системе координат. Найдем точки ее пересечения с осями координат: с осью ОХ : , , с осью ОY: , , и с осью ОZ: , 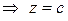. Соединим полученные точки, продолжая их во все стороны, и получим изображение плоскости.

Для нашего случая , , 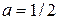, 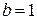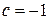. Построим эту плоскость по точкам