Решение.
1.Найдем критические точки:
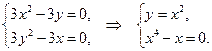
Откуда получим две критические точки 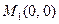 и
и  .
.
2. Производные второго порядка:
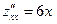 ,
, 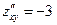 ,
,  .
.
3. В точке 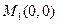
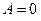 ,
, 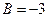 ,
, 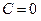 ,
,  .
.
Следовательно в этой точке минимакс.
4. В точке 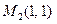
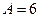 ,
, 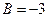 ,
,  ,
, 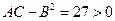 .
.
Следовательно в этой точке функция имеет минимум, так как 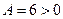 .
.
5. 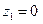 ,
, 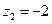 .
.
17.4. Наибольшее и наименьшее значение функции
в замкнутой области
Для того чтобы найти наименьшее и наибольшее значения функции  в ограниченной области D, следует найти значения функции в экстремальных точках и на границах области. Наибольшее и наименьшее из них являются соответственно наибольшим и наименьшим значениями функции
в ограниченной области D, следует найти значения функции в экстремальных точках и на границах области. Наибольшее и наименьшее из них являются соответственно наибольшим и наименьшим значениями функции  в области D. При отыскании этих значений на границе области следует в уравнение
в области D. При отыскании этих значений на границе области следует в уравнение  подставить уравнение границы, разрешенное относительно одной переменной и рассматривать вопрос как для функции одной переменной. Покажем это на примере.
подставить уравнение границы, разрешенное относительно одной переменной и рассматривать вопрос как для функции одной переменной. Покажем это на примере.
Пример 17.6. Найти наибольшее и наименьшее значение функции
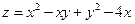
в замкнутой области D, заданной системой неравенств 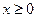 ,
, 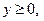
 . Сделать чертеж.
. Сделать чертеж.
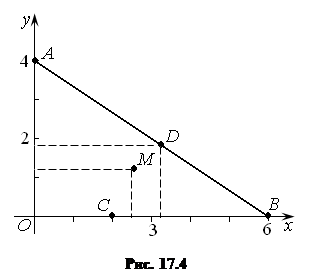 Решение. Сделаем чертеж области D. Она ограничена сторонами треугольника АОВ, причем уравнение АВ:
Решение. Сделаем чертеж области D. Она ограничена сторонами треугольника АОВ, причем уравнение АВ:  , уравнение ОВ:
, уравнение ОВ: 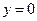 , уравнение АВ:
, уравнение АВ: 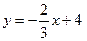 (рис. 17.4).
(рис. 17.4).
Дальнейшее решение проведем по плану:
1. Найдем критические точки, в которых частные производные равны нулю:
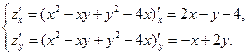
Приравняем их нулю: 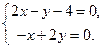
Решив эту систему, получим 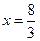 ,
, 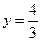 . Точка М(8/3, 4/3) принадлежит области D.
. Точка М(8/3, 4/3) принадлежит области D.
2. Определим, будет ли в этой точке экстремум, для чего воспользуемся достаточным условием (17.1) предыдущего пункта:
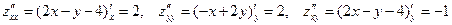 ,
,
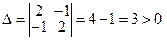 .
.
Так как 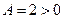 , следовательно, в точке М – min.
, следовательно, в точке М – min.
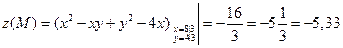 .
.
3. Найдем наименьшее и наибольшее значение функции z на границах области:
а) на границе ОА: 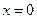 , тогда функция
, тогда функция  , где
, где 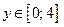 .
.
Эта функция монотонно возрастает на данном отрезке, и ее наименьшее и наибольшее значения находятся на концах отрезка в точках А и О. 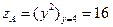 ,
, 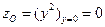 .
.
б) на границе ОВ: 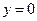 , поэтому
, поэтому 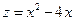 , где
, где 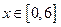 . Найдем экстремум и значения функции на концах отрезка в т. О(0,0) и точка В(6,0).
. Найдем экстремум и значения функции на концах отрезка в т. О(0,0) и точка В(6,0).
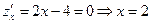
– это точка минимума точке С, т.к. парабола с поднятыми вверх ветками имеет только минимум.
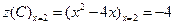 ,
, 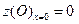 ,
, 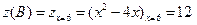 .
.
в) на границе АВ: 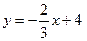 . Запишем функцию z с учетом уравнения границы:
. Запишем функцию z с учетом уравнения границы:
 и
и 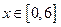 .
.
Найдем только экстремум, так как значения функции в точках А и В были найдены выше.
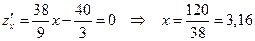 .
.
Это тоже точка минимума, назовем ее точкой D. Найдем значение функции в этой точке:
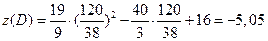 .
.
г) Запишем и сравним значения функции, во всех экстремальных и граничных точках области:
 ,
, 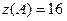 ,
, 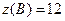 ,
, 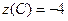 ,
, 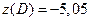 ,
, 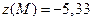 .
.
Очевидно, что наибольшее значение функция принимает в граничной точке области А и наименьшее – во внутренней точке минимума М.
Таким образом, нахождение наибольшего и наименьшего значения функции в замкнутой области свелось к функции одной переменной, с чем мы уже встречались в теме «Экстремумы функции одной переменной».
Если требуется определить наименьшее и наибольшее значение функции многих переменных, которые связаны друг с другом какими-то добавочными условиями, то эта задача так и называется задачей на условные экстремумы. Она выходит за рамки рассматриваемого курса. Ее можно найти в рекомендуемой литературе.
17.5. Подбор параметров для эмпирических формул простейшего
вида по методу наименьших квадратов
Рассматривая функции одной и многих переменных по способам их задания, мы всегда переходили от одного способа к другому по цепочке
формула , причем взаимный переход двух последних способов осуществлялся достаточно просто. Составление уравнения, связывающего две переменные величины, полученные при проведении опытов, натолкнулось на трудности двух видов.
, причем взаимный переход двух последних способов осуществлялся достаточно просто. Составление уравнения, связывающего две переменные величины, полученные при проведении опытов, натолкнулось на трудности двух видов.
1. Определение вида аппроксимирующей (приближенной) функции – линейной, степенной, гиперболической и т.д. Ее можно было решить из логики процесса: из теоретических соображений или на основании характера расположения точек, соответствующих экспериментальным данным.
2. Определение коэффициентов выбранной зависимости, чтобы она в каком-то смысле наилучшим образом описывала рассматриваемый процесс.
Для решения второй задачи разработаны различные методы корреляционного и дисперсионного анализа, в основе которых лежат два требования, предъявляемых к выбранной функции:
3. Сумма отклонений эмпирических данных от расчетных должна быть равна нулю:
 . (17.2)
. (17.2)
Это требование было необходимым, но недостаточным для того, чтобы определить коэффициенты искомой функции. Поэтому выдвинули второе требование
4. Сумма квадратов отклонений эмпирических данных от расчетных должна быть наименьшей:
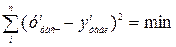 . (17.3)
. (17.3)
Отсюда название метода – метод наименьших квадратов. Покажем его действие на примере.
Пусть в результате эксперимента получено n значений функции у при соответствующих значения х. Результаты записаны в таблицу.