рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Философия
- /
- КОНСПЕКТ ЛЕКЦІЙ З КУРСУ ЛІНІЙНОЇ АЛГЕБРИ ТА АНАЛІТИЧНОЇ ГЕОМЕТРІЇ
Реферат Курсовая Конспект
КОНСПЕКТ ЛЕКЦІЙ З КУРСУ ЛІНІЙНОЇ АЛГЕБРИ ТА АНАЛІТИЧНОЇ ГЕОМЕТРІЇ
КОНСПЕКТ ЛЕКЦІЙ З КУРСУ ЛІНІЙНОЇ АЛГЕБРИ ТА АНАЛІТИЧНОЇ ГЕОМЕТРІЇ - раздел Философия, Міністерство Освіти І Науки України Кіровоградський Національний Тех...
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
КІРОВОГРАДСЬКИЙ НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ
ФАКУЛЬТЕТ ПРОЕКТУВАННЯ І ЕКСПЛУАТАЦІЇ МАШИН
КАФЕДРА ВИЩОЇ МАТЕМАТИКИ ТА ФІЗИКИ
КОНСПЕКТ ЛЕКЦІЙ З КУРСУ ЛІНІЙНОЇ АЛГЕБРИ ТА АНАЛІТИЧНОЇ ГЕОМЕТРІЇ
Методичні вказівки для студентів технічних спеціальностей КІРОВОГРАДОрганізація навчального процесу за кредитно-модульною системою
Модуль І. Матриці. Визначники. Системи лінійних рівнянь. № тижня Теми лекцій Теми практичних занять … Модуль ІІ. Векторна алгебра. 5.…Розділ I. ЕЛЕМЕНТИ ЛІНІЙНОЇ АЛГЕБРИ
Лекція 1
МАТРИЦІ
Основні поняття
Матрицю позначають наступним чином:Дії над матрицями
Сумою двох матриць і називається матриця така, що , де . Сума трьох матриць – це матриця, яка отримується послідовним додаванням даних… Аналогічно визначається для .Транспонування матриць
Матрицю, транспоновану до матриці , позначають . Операція знаходження матриці, транспонованої до даної, називається… Якщо – матриця розмірів , то має розміри .Лекція 2
ВИЗНАЧНИКИ
Основні поняття
1. , : . 2. , :Властивості визначників
1.Визначник матриці, транспонованої до даної, рівний визначнику даної матриці: Дійсно,Лекції 3–4
НЕВИРОДЖЕНІ МАТРИЦІ
Основні поняття
. Квадратна матриця називається невиродженою, якщо її визначник, в протилежному… Матрицею, союзною до матриці , називається матрицяОбернена матриця
. (3.1) Теорема 3.1. Будь-яка невироджена матриця має обернену. Доведення. Знайдемо добуток матриць і :Ранг матриці
. Виділимо в ній рядків і стовпців . З елементів, що стоять на перетині… Найбільший з порядків мінорів даної матриці, відмінних від нуля, називають рангом матриці і позначають .СИСТЕМИ ЛІНІЙНИХ РІВНЯНЬ
Основні поняття
(4.1) де числа , , називаються коефіцієнтами системи, числа – вільними членами; –… МатрицяРозв’язання невироджених лінійних систем
(4.3) або в матричній формі . Основна матриця А такої системи квадратна. Визначник цієї матриціРозв’язання довільних лінійних систем. Теорема Кронекера-Капеллі
Нехай дана довільна система т лінійних рівнянь з п невідомими
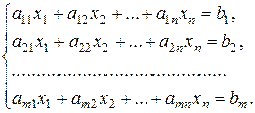
Відповідь на питання щодо сумісності цієї системи дає терема Кронекера-Капеллі:
Теорема 4.1. Система лінійних алгебраїчних рівнянь сумісна тоді і тільки тоді, коли ранг розширеної матриці системи рівний рангу основної матриці.
Приймемо її без доведення.
Правила знаходження всіх розв’язків сумісної системи лінійних рівнянь випливають з наступних теорем:
Теорема 4.2. Якщо ранг сумісної системи рівний кількості невідомих, то система має єдиний розв’язок.
Теорема 4.3.Якщо ранг сумісної системи менший кількості невідомих, то система має безліч розв’язків.
Правило розв’язання довільних лінійних систем.
2. Якщо , то система сумісна. Знайти базисний мінор порядку . Взяти рівнянь, з коефіцієнтів яких складений базисний мінор (інші рівняння відкинути).… 3. Виразити базисні невідомі через вільні. Отримаємо загальний розв’язок… 4. Надаючи вільним невідомим довільних значень, отримаємо відповідні значення базисних невідомих. Таким чином можна…Розв’язання лінійних систем методом Гауса
Нехай дана система т лінійних рівнянь з п невідомими (4.6) Процес розв’язання за методом Гауса складається з двох етапів. На першому етапі (прямий хід) система зводиться до…Розділ ІI. ЕЛЕМЕНТИ ВЕКТОРНОЇ АЛГЕБРИ
Лекція 5
ВЕКТОРИ
Основні поняття
Довжиною або модулем вектора називається довжина відрізка, на якому побудований вектор, і позначається або . Вектор, довжина якого рівна нулю, називається нульовим і позначається .… Вектор, довжина якого рівна одиниці, називається одиничним і позначається . Одиничний вектор, напрямок якого співпадає…Лінійні операції над векторами
Нехай і – два довільні вектори (рис. 5.2). Тоді вектор називається сумою векторів і та позначається . Це правило додавання векторів називають… Суму двох векторів можна знайти і за правилом паралелограма (рис. 5.3).Розклад вектора за базисом
Вектор , де – числа,Лінійні операції над векторами в координатній формі
Сума векторів.Запишемо суму векторів або, згідно властивостям лінійних операцій над векторами,Декартова прямокутна система координат
Сукупність точки О і ортонормованого базису називається декартовою прямокутною системою координат в просторі. Точку О називають початком координат.… Декартову прямокутну систему координат позначають або .Поділ відрізка в даному відношенні
Нехай в системі координат дано точки , . Знайдемо на прямій координати точки , що ділить відрізок у відношенні . Розглянемо вектори , . Так як , то ; ; . З цих рівностей отримаємо: ; ; . (5.6)Лекція 6
ДОБУТКИ ВЕКТОРІВ
Скалярний добуток векторів
Якщо хоча б один із двох даних векторів нульовий, то їх скалярний добуток за означенням вважається рівним нулю. Позначається або , або . Таким чином, за означенням, , (6.1)Властивості скалярного добутку.
Справедливість цієї властивості випливає з означення. 2. . Доведення. .Векторний добуток векторів
1) і , тобто перпендикулярний векторам і ; 2) направлений так, що вектори , , утворюють праву трійку; 3) має довжину, що дорівнює добутку довжин цих векторів на синус кута між ними, тобто , де .Властивості векторного добутку.
Справедливість цієї властивості випливає з означення. 2. . Доведення. Нехай . Вектор перпендикулярний векторам і (вектори і лежать в одній площині). Вектор також…Мішаний добуток векторів
Мішаний добуток позначається . Отже, .Властивості мішаного добутку.
Дійсно, в цьому випадку не змінюється ні об’єм паралелепіпеда, ні орієнтація векторів. 2. . Доведення. Так як за властивістю 1 і скалярний добуток не зміниться при перестановці векторів, тобто , то .Розділ ІIІ. ЕЛЕМЕНТИ АНАЛІТИЧНОЇ ГЕОМЕТРІЇ
Лекції 7–8
ЛІНІЇ НА ПЛОЩИНІ, ПОВЕРХНІ І ЛІНІЇ В ПРОСТОРІ
Рівняння лінії на площині
Введення на площині системи координат дозволяє визначити положення лінії на площині за допомогою рівняння, що пов’язує координати точок лінії. Рівнянням лінії на площині називається таке рівняння з двома змінними, якому… Координати і довільної точки, що входять в рівняння лінії, називаються поточними координатами.Рівняння поверхні та лінії в просторі
Координати , і довільної точки, що входять в рівняння поверхні, називаються поточними координатами. Приклад 7.3.Скласти рівняння сфери радіуса з центром в початку координат. Розв’язок. Як відомо, сфера – це множина точок простору, рівновіддалених від даної точки, яку називають центром.…ПЛОЩИНА, ПРЯМА В ПРОСТОРІ І НА ПЛОЩИНІ
Загальне рівняння площини
Ненульовий вектор, перпендикулярний до площини, називають нормальним вектором цієї площини. Для довільної точки площини і тільки для точок даної площини вектор , тому їх… . (8.1)Загальне рівняння прямої на площині
Ненульовий вектор, перпендикулярний до прямої, називають нормальним вектором… Для довільної точки прямої і тільки для точок даної прямої вектор . Записавши умову перпендикулярності цих векторів в…Канонічні і параметричні рівняння прямої. Рівняння прямої з кутовим коефіцієнтом
Ненульовий вектор, паралельний до прямої, називають напрямним вектором цієї… Для довільної точки прямої і тільки для точок даної прямої вектор . Записавши умову паралельності цих векторів в…Загальні рівняння прямої в просторі
Система рівнянь (8.11) визначає пряму лінію в просторі.Рівняння прямої, що проходить через дві точки
В якості напрямного вектора візьмемо вектор і запишемо рівняння прямої (8.5),… . (8.12)Рівняння площини, що проходить через три точки
Для довільної точки , що належить цій площині, і тільки для точок цієї площини, вектори , , компланарні, а отже їх мішаний добуток рівний нулю,…Кут між площинами, кут між прямими, кут між прямою і площиною
і . Один із кутів , утворених площинами, рівний куту між їх нормальними векторами… . (8.17)Відстань від точки до площини і від точки до прямої на площині
Відстань від точки до площини.Нехай в системі координат задані площина і точка (рис. 8.10). Відстань від точки до цієї площини рівна модулю проекції вектора на напрямок…Умова, при якій дві прямі лежать в одній площині
, . Їх напрямні вектори відповідно і (рис.8.11). Точка лежить на прямій , а точка – на прямій . Умовою, при якій дві прямі належать одній площині, є компланарність…Пряма на площині
а) перпендикулярна до вектора ; б) паралельна до вектора ; в) утворює з віссю кут ; г) точку . 8.2. Вказати особливості розташування прямих на площині: 1) ; 3) ; 5) ;Площина
1) 3) 2) 4) . 8.7. Скласти рівняння площини, що паралельна площині і проходить через точкуПряма в просторі. Пряма і площина
Розв’язок. а) рівняння прямої складемо, використовуючи рівняння (8.12) – прямої, що проходить через дві точки: або – канонічне рівняння прямої, .Лекція 9
ЛІНІЇ ДРУГОГО ПОРЯДКУ
Еліпс
Еліпсом називається множина точок площини, сума відстаней від кожної з яких до двох даних точок цієї площини є сталою величиною, більшою від відстані між даними точками. Дані точки називаються фокусами.
Позначимо фокуси через  ,
, 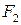 , відстань між ними
, відстань між ними 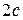 , а суму відстаней від будь-якої точки еліпса до його фокусів – через
, а суму відстаней від будь-якої точки еліпса до його фокусів – через 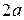 . Згідно означенню еліпса,
. Згідно означенню еліпса, 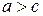 .
.
Для виведення рівняння еліпса виберемо систему координат 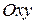 так, щоб фокуси
так, щоб фокуси  ,
, 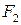 лежали на осі
лежали на осі 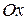 , а початок координат співпадав з серединою відрізка
, а початок координат співпадав з серединою відрізка  (рис. 9.1). Тоді фокуси матимуть координати
(рис. 9.1). Тоді фокуси матимуть координати 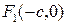 ,
, 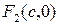 .
.
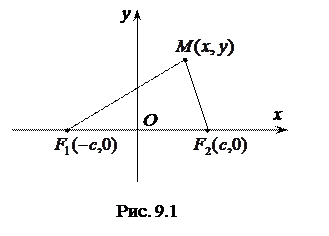
Нехай  – довільна точка еліпса. За означенням, для довільної точки еліпса і тільки для точок еліпса справедлива рівність:
– довільна точка еліпса. За означенням, для довільної точки еліпса і тільки для точок еліпса справедлива рівність:  , тобто
, тобто
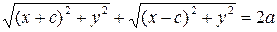
– це і є рівняння еліпса.
Приведемо отримане рівняння до більш простого вигляду. Для цього перенесемо перший доданок в праву сторону і піднесемо обидві частини рівняння до квадрату, отримаємо:
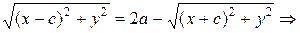

або
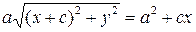 .
.
Піднесемо обидві частини отриманого рівняння до квадрату, отримаємо:
 або
або 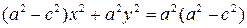 .
.
Так як 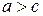 , то
, то 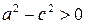 . Ввівши позначення
. Ввівши позначення  , отримаємо
, отримаємо
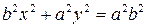
або
 (9.1)
(9.1)
Можна довести, що рівняння (9.1) рівносильне початковому рівнянню. Воно називається канонічним рівнянням еліпса.
Дослідження форми еліпса за його рівнянням.Координати 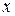 і
і  входять в рівняння (9.1) в парних степенях, тому, якщо точка
входять в рівняння (9.1) в парних степенях, тому, якщо точка 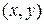 належить еліпсу, то і точки
належить еліпсу, то і точки 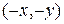 ,
, 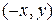 ,
,  теж йому належать. Звідси випливає, що еліпс симетричний відносно осей координат і відносно початку координат.
теж йому належать. Звідси випливає, що еліпс симетричний відносно осей координат і відносно початку координат.
Для точок, що лежать в першій координатній чверті ( ) маємо
) маємо  . З цієї рівності випливає, що
. З цієї рівності випливає, що 
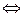
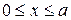 . При
. При 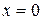 :
:  ; при
; при  :
:  . При зростанні
. При зростанні 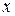 від
від 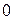 до
до 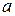 значення
значення  спадають від
спадають від 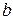 до
до 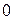 .
.

Побудуємо еліпс в першій координатній чверті і, враховуючи симетрію, відобразимо побудовану частину відносно осей координат (рис. 9.2).
Центр симетрії  називають центром еліпса. Точки
називають центром еліпса. Точки 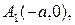
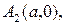
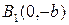 ,
,  – точки перетину еліпса з осями координат називають вершинами еліпса. Відрізок
– точки перетину еліпса з осями координат називають вершинами еліпса. Відрізок  , а також його довжина
, а також його довжина 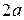 називаються великою віссю еліпса, відрізок
називаються великою віссю еліпса, відрізок 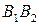 , а також його довжина
, а також його довжина 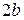 – малою віссю еліпса.
– малою віссю еліпса.
Рівняння  , де
, де 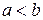 , теж є рівнянням еліпса. Фокуси такого еліпса лежать на осі
, теж є рівнянням еліпса. Фокуси такого еліпса лежать на осі 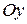 (рис. 9.3).
(рис. 9.3).

Якщо 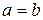 , то рівняння (9.1) набуде вигляду
, то рівняння (9.1) набуде вигляду
 (9.2)
(9.2)
– рівняння кола радіуса а з центром в  .
.
Ексцентриситет еліпса.Форма еліпса залежить від відношення 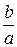 .
.
Відношення 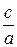 відстані між фокусами до довжини великої осі називають ексцентриситетомеліпса і позначають
відстані між фокусами до довжини великої осі називають ексцентриситетомеліпса і позначають  :
:
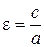 . (9.3)
. (9.3)
Так як,  , то
, то 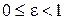 . Зауважимо: якщо
. Зауважимо: якщо 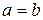 , то
, то  .
.
Підставивши в формулу (9.3)  , отримаємо
, отримаємо
 або
або 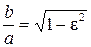 .
.
Звідси видно, що чим менше  , тим ближче відношення
, тим ближче відношення 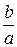 до одиниці і, отже, тим ближче форма еліпса до форми кола. Таким чином, ексцентриситет характеризує ступінь стисливості еліпса.
до одиниці і, отже, тим ближче форма еліпса до форми кола. Таким чином, ексцентриситет характеризує ступінь стисливості еліпса.
Приклад 9.1.Скласти канонічне рівняння еліпса, фокуси якого лежать на осі 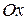 , якщо:
, якщо:
а) відстань між фокусами рівна 24, а велика піввісь рівна 16;
б) відстань між фокусами рівна 8, а ексцентриситет рівний  ;
;
в) відстань між фокусами рівна 24, а сума півосей рівна 18.
Розв’язок. а) Щоб скласти рівняння еліпса, треба знайти 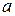 і
і 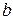 . За умовою
. За умовою  і
і 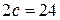 або
або 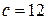 . Із співвідношення
. Із співвідношення 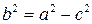 , отримаємо
, отримаємо 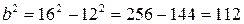 . Таким чином, шукане рівняння матиме вигляд
. Таким чином, шукане рівняння матиме вигляд
 . t
. t
б) Так як за умовою 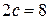 і
і  , то
, то 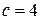 і
і 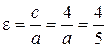 , звідки
, звідки 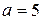 . Із співвідношення
. Із співвідношення 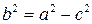 , отримаємо
, отримаємо  . Отже, шукане рівняння матиме вигляд
. Отже, шукане рівняння матиме вигляд
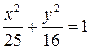 . t
. t
в) За умовою 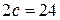 або
або 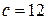 і
і 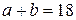 . Щоб знайти
. Щоб знайти 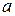 і
і 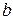 , використавши співвідношення
, використавши співвідношення 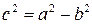 , складемо систему рівнянь:
, складемо систему рівнянь:
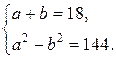
З останньої маємо
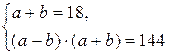
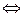

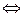
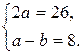
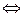
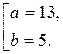 .
.
Таким чином, шукане рівняння матиме вигляд
 . t
. t
Приклад 9.2.Скласти канонічне рівняння еліпса, що проходить через точки
 ,
, 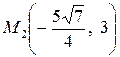 .
.
Розв’язок. Щоб скласти рівняння еліпса, треба знайти 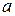 і
і 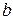 . Так як точки
. Так як точки 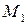 ,
,  лежать на еліпсі, то їх координати задовольняють його рівнянню. Отримаємо:
лежать на еліпсі, то їх координати задовольняють його рівнянню. Отримаємо: 
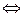
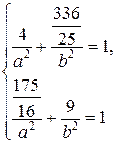
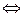
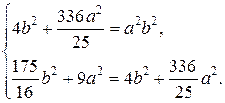
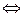
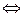
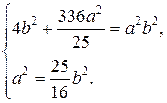
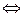
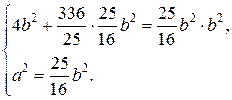
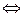
 .
.
Таким чином, шукане рівняння матиме вигляд
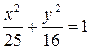 . t
. t
Гіпербола
Канонічне рівняння гіперболи. Гіперболою називається множина точок площини, модуль різниці відстаней від кожної з яких до двох даних точок цієї площини є сталою величиною, меншою від відстані між даними точками. Дані точки називаються фокусами.
Позначимо фокуси через  ,
, 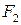 , відстань між ними
, відстань між ними 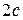 , а модуль різниці відстаней від будь-якої точки гіперболи до його фокусів – через
, а модуль різниці відстаней від будь-якої точки гіперболи до його фокусів – через 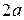 . Згідно означенню гіперболи
. Згідно означенню гіперболи  .
.
Для виведення рівняння гіперболи виберемо систему координат 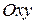 так, щоб фокуси
так, щоб фокуси  ,
, 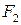 лежали на осі
лежали на осі 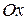 , а початок координат співпадав з серединою відрізка
, а початок координат співпадав з серединою відрізка  (рис. 9.4). Тоді фокуси матимуть координати
(рис. 9.4). Тоді фокуси матимуть координати 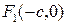 ,
, 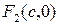 .
.
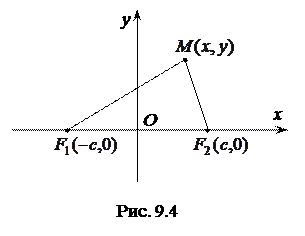
Нехай  – довільна точка гіперболи. За означенням для довільної точки гіперболи і тільки для точок гіперболи справедлива рівність:
– довільна точка гіперболи. За означенням для довільної точки гіперболи і тільки для точок гіперболи справедлива рівність:
 або
або 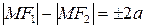 ,
,
тобто
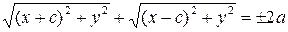
– це і є рівняння гіперболи. Приведемо отримане рівняння до більш простого вигляду, як це було зроблено для еліпса. Отримаємо:
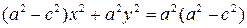 .
.
Так як  , то
, то  . Ввівши позначення
. Ввівши позначення 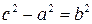 , отримаємо:
, отримаємо: 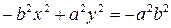 або
або
 (9.4)
(9.4)
Можна довести, що рівняння (9.4) рівносильне початковому рівнянню. Воно називається канонічним рівнянням гіперболи.
Дослідження форми гіперболи за її рівнянням.Координати 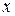 і
і  входять в рівняння (9.4) в парних степенях, тому гіпербола симетрична відносно осей координат і відносно початку координат.
входять в рівняння (9.4) в парних степенях, тому гіпербола симетрична відносно осей координат і відносно початку координат.
Для точок, що лежать в першій координатній чверті ( ) маємо
) маємо
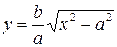 .
.
З цієї рівності випливає, що 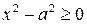
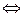
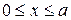 . При
. При  :
:  . При зростанні
. При зростанні 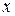 значення
значення  теж зростають, і точка
теж зростають, і точка  кривої при цьому необмежено віддаляється від осей
кривої при цьому необмежено віддаляється від осей 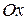 і
і 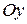 .
.
Побудуємо гіперболу в першій координатній чверті і, враховуючи симетрію, відобразимо побудовану частину відносно осей координат (рис. 9.5). Гіпербола складається з двох частин, які називаються вітками.

Центр симетрії  називають центром гіперболи. Точки
називають центром гіперболи. Точки 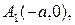
 – точки перетину гіперболи з віссю
– точки перетину гіперболи з віссю 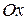 називають вершинами гіперболи. З віссю
називають вершинами гіперболи. З віссю 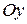 гіпербола не перетинається. Відрізок
гіпербола не перетинається. Відрізок  , а також його довжина
, а також його довжина 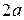 називаються дійсною віссю гіперболи, а число
називаються дійсною віссю гіперболи, а число 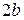 – уявною віссю гіперболи.
– уявною віссю гіперболи.
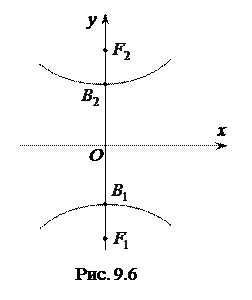
Рівняння  теж є рівнянням гіперболи. Фокуси такої гіперболи лежать на осі
теж є рівнянням гіперболи. Фокуси такої гіперболи лежать на осі 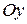 (рис. 9.6). В цьому випадку точки
(рис. 9.6). В цьому випадку точки 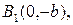
 є вершинами гіперболи, а
є вершинами гіперболи, а 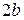 – дійсною віссю,
– дійсною віссю, 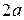 – уявною.
– уявною.
Якщо 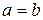 , то гіпербола називається рівносторонньою.
, то гіпербола називається рівносторонньою.
Асимптоти гіперболи.Пряма 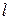 називається асимптотою необмеженої кривої
називається асимптотою необмеженої кривої 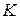 , якщо відстань
, якщо відстань  від точки
від точки 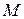 кривої
кривої 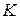 до цієї прямої прямує до нуля при необмеженому віддаленні точки
до цієї прямої прямує до нуля при необмеженому віддаленні точки 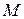 вздовж кривої
вздовж кривої 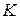 від початку координат (рис. 9.7).
від початку координат (рис. 9.7).

Покажемо, що гіпербола, задана рівнянням (9.4), має дві асимптоти:
 і
і  . (9.5)
. (9.5)
Так як прямі (9.5) і гіпербола (9.4) симетричні відносно осей координат, то достатньо розглянути тільки ті їх точки, що лежать в першій координатній чверті.
Візьмемо на прямій  точку
точку 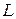 з такою ж абсцисою
з такою ж абсцисою 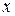 , як і в точки
, як і в точки  , що лежить на гіперболі
, що лежить на гіперболі 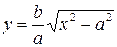 (рис. 9.8) і знайдемо різницю
(рис. 9.8) і знайдемо різницю 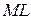 між ординатами прямої і вітки гіперболи:
між ординатами прямої і вітки гіперболи:

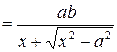 .
.
Чисельник отриманого дробу є постійною величиною, а знаменник збільшується при зростанні 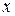 . Отже, довжина відрізка
. Отже, довжина відрізка  прямує до нуля при
прямує до нуля при  . Так як
. Так як  , то
, то  теж прямує до нуля. Таким чином, прямі
теж прямує до нуля. Таким чином, прямі
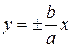
є асимптотами гіперболи.
Для гіперболи, заданої рівнянням  , асимптоти також мають вигляд (9.5).
, асимптоти також мають вигляд (9.5).
При побудові гіперболи доцільно спочатку побудувати прямокутник з центром симетрії в початку координат із сторонами 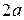 ,
, 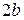 . Прямі, що проходять через протилежні вершини цього прямокутника, будуть асимптотами гіперболи.
. Прямі, що проходять через протилежні вершини цього прямокутника, будуть асимптотами гіперболи.
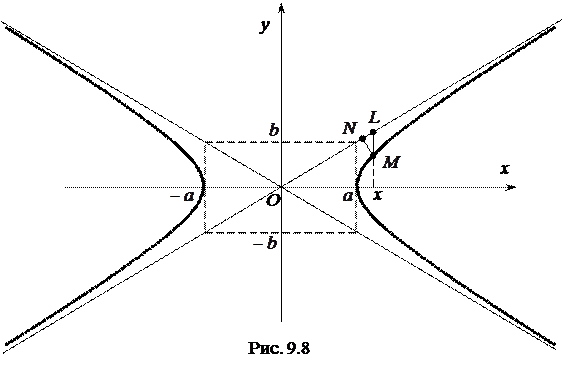
Ексцентриситет гіперболи. Відношення 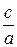 відстані між фокусами до довжини дійсної осі називають ексцентриситетомгіперболи і позначають
відстані між фокусами до довжини дійсної осі називають ексцентриситетомгіперболи і позначають  :
:
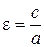 . (9.6)
. (9.6)
Так як  , то
, то  .
.
Ексцентриситет характеризує форму гіперболи. Дійсно, підставивши в формулу (9.6) 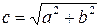 , отримаємо
, отримаємо
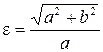 або
або  .
.
Звідси видно, що чим менше  , тим менше відношення
, тим менше відношення 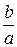 і тим менші кути між асимптотами, в яких розташована гіпербола.
і тим менші кути між асимптотами, в яких розташована гіпербола.
Якщо гіпербола задана рівнянням  , то ексцентриситет знаходимо за формулою
, то ексцентриситет знаходимо за формулою 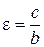 .
.
Приклад 9.3.Скласти канонічне рівняння гіперболи, фокуси якої лежать на осі 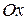 , якщо відстань між фокусами рівна 30, а дійсна вісь рівна 16.
, якщо відстань між фокусами рівна 30, а дійсна вісь рівна 16.
Розв’язок. Щоб скласти рівняння гіперболи, треба знайти 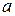 і
і 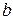 . За умовою
. За умовою  або
або  і
і  або
або 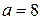 . Із співвідношення
. Із співвідношення  , отримаємо
, отримаємо 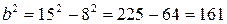 . Таким чином, шукане рівняння матиме вигляд
. Таким чином, шукане рівняння матиме вигляд
 . t
. t
Приклад 9.4.Скласти канонічне рівняння гіперболи, фокуси якої лежать на осі 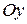 , якщо уявна вісь рівна 10, а ексцентриситет рівний
, якщо уявна вісь рівна 10, а ексцентриситет рівний 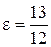 . Знайти її асимптоти.
. Знайти її асимптоти.
Розв’язок. Так як за умовою 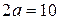 і
і 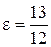 , то
, то 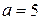 і
і 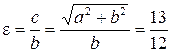 . Отримаємо:
. Отримаємо:  . Звідки
. Звідки  або
або  .
.
Отже, шукане рівняння гіперболи матиме вигляд
 ,
,
а рівняння асимптот –
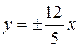 . t
. t
Парабола
Канонічне рівняння параболи. Параболою називається множина точок площини, кожна з яких однаково віддалена від даної точки і даної прямої. Дану точку називають фокусом, а дану пряму директрисою.
Позначимо фокус через  . Відстань від фокуса
. Відстань від фокуса  до директриси називається параметром параболи і позначається
до директриси називається параметром параболи і позначається  .
.
Для виведення рівняння параболи виберемо систему координат 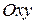 так, щоб вісь
так, щоб вісь 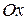 проходила через фокус
проходила через фокус  перпендикулярно директрисі в напрямку від директриси до фокуса. За початок координат виберемо середину між фокусом і точкою перетину директриси з віссю
перпендикулярно директрисі в напрямку від директриси до фокуса. За початок координат виберемо середину між фокусом і точкою перетину директриси з віссю 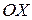 . Тоді рівняння директриси матиме вигляд:
. Тоді рівняння директриси матиме вигляд:  , а координати фокуса
, а координати фокуса  (рис. 9.9).
(рис. 9.9).
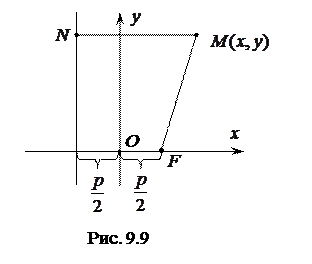
Нехай  – довільна точка параболи. Проведемо відрізок
– довільна точка параболи. Проведемо відрізок  перпендикулярно директрисі, тоді
перпендикулярно директрисі, тоді 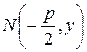 За означенням для довільної точки параболи і тільки для точок параболи справедлива рівність:
За означенням для довільної точки параболи і тільки для точок параболи справедлива рівність:
 , тобто
, тобто 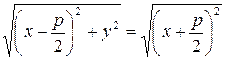
– це і є рівняння параболи. Приведемо отримане рівняння до більш простого вигляду. Для цього піднесемо обидві частини рівняння до квадрату і приведемо подібні, отримаємо:
 . (9.7)
. (9.7)
Можна довести, що рівняння (9.7) рівносильне початковому рівнянню. Воно називається канонічним рівнянням параболи.
Дослідження форми параболи за її рівнянням.Координата  входить в рівняння (9.7) в парному степені, тому парабола симетрична відносно осі
входить в рівняння (9.7) в парному степені, тому парабола симетрична відносно осі 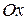 .
.
Так як 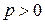 , то з рівняння (9.7) випливає, що
, то з рівняння (9.7) випливає, що  . А отже, парабола розташована справа від осі
. А отже, парабола розташована справа від осі 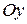 .
.
При 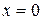 :
:  – парабола проходить через початок координат і точка
– парабола проходить через початок координат і точка  називається вершиною параболи.
називається вершиною параболи.
При зростанні 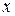 значення модуля
значення модуля  теж зростають.
теж зростають.
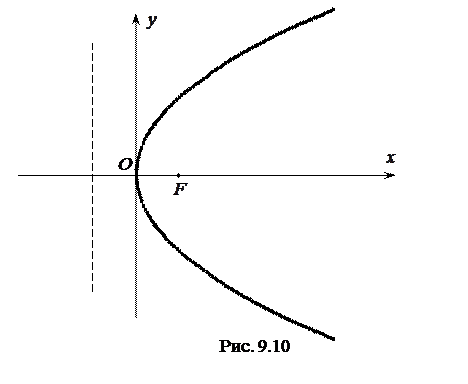
Парабола  побудована на рис. 9.10.
побудована на рис. 9.10.
Рівняння 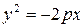 ,
, 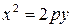 ,
, 
 теж є рівняннями параболи.
теж є рівняннями параболи.
Парабола має нескінченні вітки. Асимптот у параболи немає.
Ексцентриситет параболи вважають рівним одиниці.
Приклад 9.5.Скласти канонічне рівняння параболи, якщо вона симетрична відносно осі 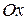 і проходить через точку
і проходить через точку 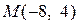 .
.
Розв’язок. Так як парабола симетрична відносно осі 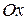 , то її рівняння має вигляд
, то її рівняння має вигляд 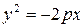
 . Підставимо координати точки
. Підставимо координати точки 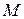 в це рівняння, отримаємо:
в це рівняння, отримаємо:  або
або 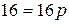 , звідки
, звідки 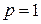 . Отже,
. Отже,  – шукане рівняння. t
– шукане рівняння. t
Еліпс, гіпербола, парабола з осями, паралельними осям координат
Перейдемо від системи координат до нової системи координат за допомогою паралельного переносу. При цьому початок координат перейде в точку , а осі ,… , . (9.8)ВІДПОВІДІ
1.3. а) , б) , в) , г) . 1.4. а) , б) . 1.6.а),б)102,в). 2.1.а) 31,б) 260. 2.2.а) 0, б) 0, в) -25600. 2.3. . 2.4. 11.А),б)не існує,в),г)не існує.
3.2.а)3, б) 3, в) 1. 4.1. 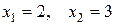 . 4.2.
. 4.2. 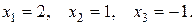
5.1. 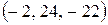 . 5.2.а) так, б) так, в) ні. 5.3.а) так, б) так.
. 5.2.а) так, б) так, в) ні. 5.3.а) так, б) так.
5.4.  . 5.5.
. 5.5. 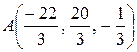 . 5.6.
. 5.6. 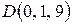 . 6.1.0.6.2.
. 6.1.0.6.2.  .
.
А) ні; б) ні. 7.1. . 7.2. Точка В. 7.3. б) і в). 7.4.. 7.5. .8.1.а),б),в),г). 8.2.а) проходить через початок координат, б) паралельна осі , в) паралельна осі , г) співпадає з віссю , д) відтинає відрізки довжиною 2 і 7 на осях , відповідно, е)співпадає звіссю. 8.4.а),б),в),г). 8.5. .
8.6.1) проходить через початок координат, 2) проходить через вісь 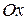 ,
,
3) паралельна осі 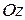 , 4) паралельнакоординатній площині
, 4) паралельнакоординатній площині . 8.7.
. 8.7. 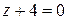 . 8.8.
. 8.8. 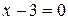 . 8.9.
. 8.9. 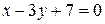 . 8.10.-15, -10 і 6.
. 8.10.-15, -10 і 6.
8.11. . 8.12. . 8.13. .
8.15. . 8.16. . 8.17. .
8.18.  . 9.1.
. 9.1. 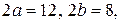
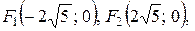
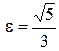 . 9.2.а)
. 9.2.а) 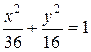 , б)
, б) 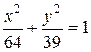 , в)
, в) 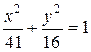 , г)
, г)  ,
,
д) 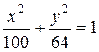 , е)
, е)  . 9.3.
. 9.3.  . 9.4.
. 9.4. 
 . 9.5.
. 9.5. 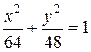 . 9.6.
. 9.6.  або
або 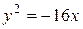 . 9.7.
. 9.7. 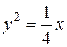 .
.
Індивідуальні завдання
1. . 2. . 3. .Тестові завдання з лінійної алгебри
a) ; b) ; c) ; d) ; e) інша відповідь. 2. Яка з матриць є діагональною:ВІДПОВІДІ
| 1. e. 2. c. 3. b. 4. e. 5. a. | 6. c. 7. a. 8. a. 9. c. 10. a. | 11. b. 12. d. 13. b. 14. b. 15. a. | 16.d. 17.c. 18.d. 19.a. 20.b. |
Тестові завдання з аналітичної геометрії
a) ; b) ; c) ; d) ; e) інша відповідь. 2. Знайти довжину вектора :ВІДПОВІДІ
| 1. c. 2. b. 3. d. 4. a. 5. c. | 6. d. 7. a. 8. c. 9. c. 10. b. | 11. d. 12. a. 13. e. 14. a. 15. b. | 16.с. 17.c. 18.b. 19.e. 20.с. |
– Конец работы –
Используемые теги: Конспект, лекцій, курсу, лінійної, алгебри, аналітичної, геометрії0.099
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: КОНСПЕКТ ЛЕКЦІЙ З КУРСУ ЛІНІЙНОЇ АЛГЕБРИ ТА АНАЛІТИЧНОЇ ГЕОМЕТРІЇ
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов