рефераты конспекты курсовые дипломные лекции шпоры

  • Раздел Философия
  •  / 
  • Лінійні операції над векторами в координатній формі

Реферат Курсовая Конспект

Лінійні операції над векторами в координатній формі

Лінійні операції над векторами в координатній формі - раздел Философия, КОНСПЕКТ ЛЕКЦІЙ З КУРСУ ЛІНІЙНОЇ АЛГЕБРИ ТА АНАЛІТИЧНОЇ ГЕОМЕТРІЇ Нехай Заданий Базис ...

Нехай заданий базис 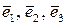і вектори 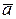(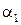,,), 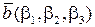або, що те ж саме, , .

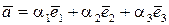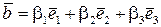Сума векторів.Запишемо суму векторів

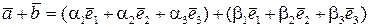
або, згідно властивостям лінійних операцій над векторами,

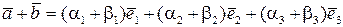. (5.3)

Таким чином, при додаванні векторів їх відповідні координати додаються.

Добуток вектора на число.Помножимо вектор 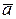на число :

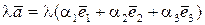
або

. (5.4)

Тобто при множенні вектора на число координати вектора множаться на це число.

Приклад 5.1.В базисі 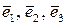дано вектори , . Знайти вектор .

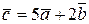Розв’язок. Згідно формулам (5.3), (5.4)

.

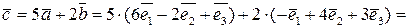
Відповідь: t

Рівність векторів.З означення вектора як направленого відрізка, який можна переміщати в просторі паралельно самому собі, випливає, що два вектори 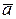і 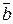рівні тоді і тільки тоді, коли рівні їх координати:

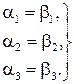
Колінеарність векторів.Вияснимо умови колінеарності векторів 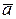і 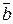, заданих своїми координатами.

Так як 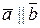, то за властивостями добутку вектора на число можна записати , де – деяке число, тобто

.

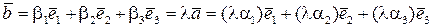Звідси 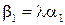, , 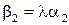, тобт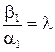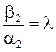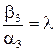о , , або

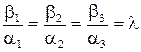. (5.5)

Таким чином, координати колінеарних векторів пропорційні. Справедливе і обернене твердження: вектори, що мають пропорційні координати, колінеарні.

Зауваження. Співвідношення (5.5) умовно записуватимемо і у випадку, коли серед чисел 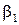, , 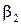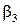є рівні нулю.

Нехай на площині заданий базис 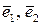і вектори 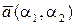, 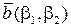. В цьому випадку мають місце формули, аналогічні формулам (5.3) – (5.5).

Приклад 5.2.Перевірити, чи колінеарні вектори 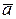і 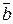, задані в базисі :

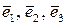а) , ; б) , .

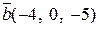Розв’язок. Згідно формули (5.5):

а) 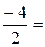, а отже .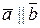

б) .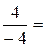

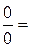
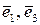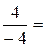
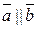Так як друга координата в обох векторів рівна нулю, то їх можна розглядати як вектори, задані на площині в базисі , а отже і . t

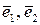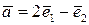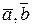Приклад 5.3.В базисі дано вектори , . Показати, що вектори утворюють базис, і знайти координати вектора в базисі .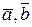

Розв’язок. Якщо два вектори утворюють базис, то вони неколінеарні. Згідно формули (5.5):

,

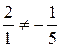а отже вектори 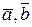неколінеарні і утворюють базис.

В новому базисі 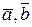вектор 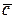можна представити у вигляді лінійної комбінації

,

де коефіцієнти , 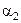– невідомі і є координатами вектора 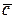в базисі .

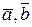Знайдемо ці координати. Для цього розпишемо розклад вектора 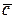в координатній формі:

,

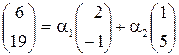що рівносильно системі двох лінійних рівнянь з двома невідомими

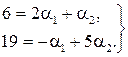
Розв’яжемо цю систему за формулами Крамера:

; .

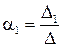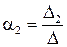Обчислимо визначники:

;

;

.

Отримаємо ; .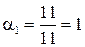

Відповідь: . t

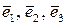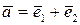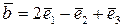Приклад 5.4.В базисі дано вектори , , . Показати, що вектори 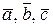утворюють базис, і знайти координати вектора 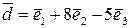в базисі .

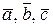Розв’язок. Якщо три вектори утворюють базис, то жоден з них не є лінійною комбінацією двох інших. Тоді визначник, складений з координат цих векторів, відмінний від нуля, так як лінійні операції над векторами зводяться до відповідних лінійних операцій над їх координатами. Обчислимо цей визначник:

.

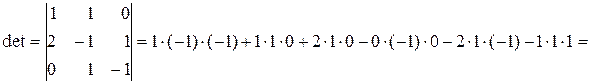
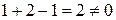Отже, вектори 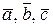утворюють базис.

В новому базисі 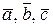вектор можна представити у вигляді лінійної комбінації

,

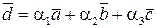де коефіцієнти 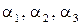– невідомі і є координатами вектора в базисі .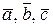

Знайдемо ці координати. Для цього розпишемо розклад вектора в координатній формі:

,

що рівносильно системі трьох лінійних рівнянь з трьома невідомими

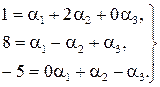
Розв’яжемо цю систему за формулами Крамера:

; ; .

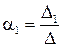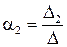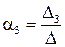Очевидно, що визначник 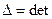як визначник транспонованої матриці:

.

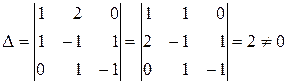Обчислимо

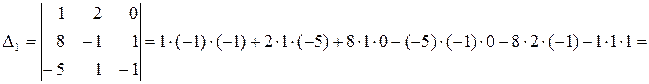
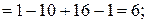
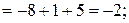
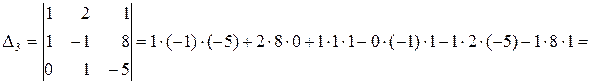
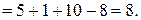
Отримаємо ; ;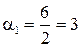

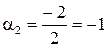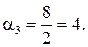
Відповідь: 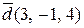. t

 

Развернуть
Открыть в широком формате

– Конец работы –

Эта тема принадлежит разделу:

КОНСПЕКТ ЛЕКЦІЙ З КУРСУ ЛІНІЙНОЇ АЛГЕБРИ ТА АНАЛІТИЧНОЇ ГЕОМЕТРІЇ

КІРОВОГРАДСЬКИЙ НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ... ФАКУЛЬТЕТ ПРОЕКТУВАННЯ І ЕКСПЛУАТАЦІЇ МАШИН... КАФЕДРА ВИЩОЇ МАТЕМАТИКИ ТА ФІЗИКИ...

Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Лінійні операції над векторами в координатній формі

Что будем делать с полученным материалом:

Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:

Все темы данного раздела:

КОНСПЕКТ ЛЕКЦІЙ З КУРСУ ЛІНІЙНОЇ АЛГЕБРИ ТА АНАЛІТИЧНОЇ ГЕОМЕТРІЇ
КРЕДИТНО-МОДУЛЬНА СИСТЕМА Методичні вказівки для студентів технічних спеціальностей   КІРОВОГРАД   Конспект лекцій з курсу лінійної ал

Організація навчального процесу за кредитно-модульною системою
ЛІНІЙНА АЛГЕБРА ТА АНАЛІТИЧНА ГЕОМЕТРІЯ   Модуль І. Матриці. Визначники. Системи лінійних рівнянь. № тижня Теми

Основні поняття
Матрицею (числовою матрицею) називається прямокутна таблиця складена з чи

Дії над матрицями
Додавання. Дія додавання матриць вводиться тільки для матриць однакових розмірів. Сумою двох матриць

Транспонування матриць
Матриця, отримана з даної заміною кожного її рядка (стовпчика) стовпчиком (рядком) з тим же номером, називається транспонованою до даної. Матрицю, транспоновану до

Основні поняття
Квадратній матриці А порядку п можна поставити у відповідність число, яке називається її визначником або детермінантом і познача

Властивості визначників
Сформулюємо основні властивості визначників, які справедливі для визначників всіх порядків. Деякі з них пояснимо на визначниках 3-го порядку. 1.Визначник матриці, транс

Основні поняття
Нехай – квадратна матриця

Обернена матриця
Матриця називається оберненоюдо матриці

Ранг матриці
Розглянемо матрицю розмірів

Основні поняття
Системою т лінійних алгебраїчних рівнянь з п невідомими називається система вигляду

Розв’язання невироджених лінійних систем
Нехай дана система п лінійних рівнянь з п невідомими: (4.3) або в ма

Правило розв’язання довільних лінійних систем.
1. Знайти ранги основної і розширеної матриць системи. Якщо , то система несумісна. 2. Якщо

Розв’язання лінійних систем методом Гауса
Універсальним методом розв’язання систем лінійних алгебраїчних рівнянь є метод Гауса, який полягає в послідовному виключенні змінних. Нехай дана система т лінійних рівнянь з п

Основні поняття
Вектор – це направлений відрізок, тобто відрізок, який має певну довжину і певний напрямок. Якщо А – початок вектора, а В – його кінець, то вектор позначають

Лінійні операції над векторами
Лінійними операціями над векторами називають додавання і множення векторів на число. Нехай

Розклад вектора за базисом
Нехай дано вектори . Вектор

Декартова прямокутна система координат
Нехай в просторі дано точку О і ортонормований базис, який позначатимемо . Сукупніст

Поділ відрізка в даному відношенні
Розділити відрізок у відношенні

Скалярний добуток векторів
Означення скалярного добутку. Скалярним добутком двох ненульових векторів

Властивості скалярного добутку.
1. . Справедливість цієї властивості випливає з означення. 2.

Векторний добуток векторів
Означення векторного добутку. Векторним добутком двох неколінеарних векторів

Властивості векторного добутку.
1.

Мішаний добуток векторів
Означення мішаного добутку. Мішаним добутком трьох векторів ,

Властивості мішаного добутку.
1. Мішаний добуток не змінюється при циклічній перестановці його множників: . Дійсно, в цьо

Рівняння лінії на площині
Лінія на площині часто задається як множина точок, що має деякі геометричні властивості, які характерні тільки для цієї множини. Введення на площині системи координат дозволяє визначити по

Рівняння поверхні та лінії в просторі
Рівнянням поверхні в заданій системі координат називаєт

Загальне рівняння площини
    Пол

Загальне рівняння прямої на площині
Положення прямої на площині

Канонічні і параметричні рівняння прямої. Рівняння прямої з кутовим коефіцієнтом
Канонічні і параметричні рівняння прямої. Положення прямої в просторі і системі коо

Загальні рівняння прямої в просторі
Нехай задані дві непаралельні площини і

Рівняння прямої, що проходить через дві точки
Нехай в системі координат задані дві точки

Рівняння площини, що проходить через три точки
Нехай в системі координат задані три точки

Кут між площинами, кут між прямими, кут між прямою і площиною
Кут між площинами.Нехай задані дві площини і

Відстань від точки до площини і від точки до прямої на площині
Відстань від точки до площини.Нехай в системі координат

Умова, при якій дві прямі лежать в одній площині
Нехай прямі і

Пряма на площині
8.1 Скласти рівняння прямої, що проходить через точку і: а) перпендикулярна до ве

Площина
8.6. Вказати особливості розташування площин відносно системи координат : 1)

Пряма в просторі. Пряма і площина
8.15. Дано чотири точки ,

Еліпс, гіпербола, парабола з осями, паралельними осям координат
Розглянемо еліпс з центром в точці з осями, паралельними осям координат (рис. 9.11). Перейд

ВІДПОВІДІ
1.1. а) 23, б)

Індивідуальні завдання
1. Знайти матрицю , де

Тестові завдання з лінійної алгебри
1. Яка з матриць є трикутною: a)

Тестові завдання з аналітичної геометрії
1. Вказати рівняння площини, що проходить через точку перпендикулярно до вектора

Хотите получать на электронную почту самые свежие новости?
Education Insider Sample
Подпишитесь на Нашу рассылку
Наша политика приватности обеспечивает 100% безопасность и анонимность Ваших E-Mail
Реклама
Соответствующий теме материал
  • Похожее
  • Популярное
  • Облако тегов
  • Здесь
  • Временно
  • Пусто
Теги