Метод статистичних випробувань

 

Метод статистичних випробувань — це числовий метод математичного моделювання випадкових величин, який передбачає безпосереднє включення випадкового фактора в процес моделювання і є його істотним елементом. Вплив випадкових факторів на систему моделюється за допомогою випадкових чисел. Результатом моделювання є випадкові процеси або величини, які характеризують систему, що моделюється. Щоб їх імовірнісні характеристики (імовірність деяких подій, математичне сподівання, дисперсія випадкових величин, імовірності попадання випадкової величини в задану область та ін.) співпадали з аналогічними параметрами реальної системи або процесу під час моделювання потрібно багато раз провести випробування побудованої ймовірнісної моделі. А потім здійснити статистичну обробку результатів моделювання з метою визначення шуканих характеристик розглядуваного процесу. На практиці метод статистичних випробувань доцільно використовувати в таких випадках, коли:

- розв'язувати задачу цим методом простіше, ніж будь-яким іншим;

- досліджується система, функціонування якої визначається багатьма ймовірнісними параметрами елементарних явищ;

- важко або неможливо побудувати аналітичну ймовірнісну модель системи.

Важливою властивістю цього методу є те, що для звичайних числових методів обсяг обчислень зростає в разі збільшення розмірності задачі приблизно як показникова функція розмірності задачі, а для методу статистичних випробувань — лише як лінійна функція розмірності.

Незалежно від типу досліджуваної моделі системи, застосовуючи метод статистичних випробувань, необхідно виконати такі кроки.

1 Визначити, що являтиме собою кожне випробування і зазначити, яке випробування буде успішним, а яке — ні.

2 Обчислити кількість випробувань, які необхідно провести, щоб отримати результати із заданою точністю, і провести ці випробування.

3 Виконати статистичну обробку результатів випробувань та обчислити оцінки необхідних статистичних характеристик.

4 Проаналізувати точність отриманих статистичних характеристик.

У методі статистичних випробувань особливе значення відіграють випадкові числа, рівномірно розподілені в інтервалі [0, 1]. Для використання методу статистичних випробувань необхідно:

- генерувати випадкові числа, рівномірно розподілені в інтервалі [0, 1];

- описувати модельовані випадкові явища функціями розподілу ймовірностей та ймовірнісними процесами;

- мати методи отримання випадкових величин функцій розподілу ймовірностей (дискретних і неперервних), які базуються на випадкових числах, рівномірно розподілених у інтервалі [0, 1];

- оцінювати статистичні характеристики випадкових величин з отриманих за допомогою методу статистичних випробувань чисел вибіркової послідовності;

- визначати точність отриманих статистичних оцінок як функцій від числа випробувань.

Випадкові числа, рівномірно розподілені в інтервалі [0, 1], мають дві основні властивості:

1 Якщо r_і (і = 1,2,3,...) — випадкові числа, рівномірно розподілені в інтервалі [0,1], то їх кумулятивний розподіл F (за визначенням F(r_i) = Р (r_i- < r)), задовольняє співвідношенням:

 

 

Слід зауважити, що теоретично ці випадкові числа повинні бути вибірковими значеннями неперервної величини з функцією щільності, визначеною таким чином:

 

Насправді ж під час комп'ютерного моделювання використовуються тільки дискретні значення, в яких після десяткової коми є фіксована кількість десяткових знаків.

2 Випадкові числа r₁, r₂, ..., r_n є незалежними, якщо їх сумісний кумулятивний розподіл G можна подати як добуток окремих функцій розподілу:

 

 

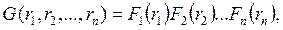
або, враховуючи, що n випадкових чисел мають однакові розподіли, можна записати:

 

.

 

Розглянемо кілька задач, для розв'язування яких можна застосувати метод статистичних випробувань.

Приклад 1. Необхідно знайти площу фігури (рис. 3.1), обмежену функцією у =f(x) та осями координат Ох і Оу.

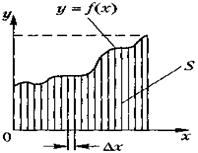
Рисунок 3.1 - Схема обчислення інтеграла

 

У числових методах для інтегрування використовується наближене зображення інтеграла у вигляді квадратурної формули. Одним із найпростіших є метод прямокутників. У разі використання методу прямокутників інтеграл апроксимується такою формулою:

 

 

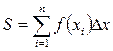
Ця формула і є формулою числового інтегрування. Чим більша кількість інтервалів п і менший крок Δх, тим точніше можна обчислити площу S.

Тепер покажемо, як можна розв'язати цю задачу за допомогою методу статистичних випробувань. Спочатку пронормуємо функцію у = f(x) так, щоб уписати її в одиничний квадрат. Припустимо, що ξ — деяка випадкова величина, рівномірно розподілена в інтервалі [0, 1]. Тоді ймовірність попадання значення ξ в будь-який відрізок [а, b] є [0, 1] буде залежати тільки від довжини відрізка [а, b], а не від місця його розташування в інтервалі [0, 1], тобто ймовірність того, що вибіркове значення випадкової величини ξ потрапить у деякий відрізок 0 < =а <= b <= 1, дорівнюватиме довжині цього відрізка: Ρ(α <= ξ <= b) = ∫dξ , = b — a.

Будемо використовувати одне значення випадкової величини ξ для визначення координати х_i а друге — для визначення координати y_i;. Таким чином, пара значень випадкової величини ξ задаватиме на площині точку з координатами (x_i, у_i). Ймовірність попадання цієї точки в деяку область одиничного квадрата пропорційна площі цієї області та не залежить від місця розташування області в одиничному квадраті.

Проведемо N випробувань. Випробування будемо вважати успішним, якщо точка з координатами (x_i, у_i) потрапить в область під кривою у = f(x) або на неї. Підрахуємо кількість успішних випробувань, позначимо їх через т і визначимо частість успішних випробувань — m/Ν. На рисунку 3.1 видно, що у разі збільшення кількості випробувань ця величина наближається до ймовірності попадання точки в заштриховану область Ρ = S/S_од.кв= S = m/N, де S_од.кв — площа одиничного квадрата. Таким чином, згідно з теоремою Бернуллі

 

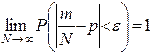
У разі прямування кількості випробувань N до нескінченності частість успішних випробувань буде відрізнятись від імовірності ρ на нескінченно малу величину ε. Отже, можна вважати, що m/Ν — наближене значення шуканої площі S.

Цей приклад демонструє те, як метод статистичних випробувань може бути використано під час розв'язування детермінованих задач. На практиці такий підхід використовується для знаходження площ або об'ємів деяких багатовимірних фігур, які утворюються у випадку перетину різних геометричних тіл. У цьому разі число випробувань Ν, які необхідно провести для обчислення площі або об'єму, не залежить від кратності визначеного інтеграла.

Приклад 2.Припустимо, що чотири стрільці одночасно стріляють у рухому ціль. Імовірність влучення в ціль кожним стрільцем дорівнює 0,5. Ціль вважається враженою, якщо в неї влучило два або більше стрільців. Потрібно знайти ймовірність ураження цілі.

Використовуючи методи теорії ймовірностей, цю задачу досить легко розв'язати аналітично. Дійсно, імовірність ураження цілі одним пострілом р_вр = 1 - р_невр, де р_невр — імовірність того, що ціль не буде вражена взагалі, визначається за формулою:

 

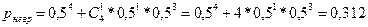
Звідси ймовірність ураження цілі

 

 

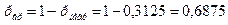
Тепер покажемо, як розв'язати цю задачу за допомогою методу статистичних випробувань. Процедуру розіграшу можна реалізувати, одночасно підкидаючи чотири монети. Для моделювання підкидання однієї монети використовується одне значення r_i. Якщо r_i < р, вважаємо, що монета падає лицевим боком, і, таким чином, стрілець влучив у ціль. Інакше вважаємо, що стрілець промахнувся. Одне випробування — це підкидання чотирьох монет. Зробимо N випробувань і позначимо через т число успішних випробувань (дві або більше монет упали лицевим боком, що свідчить про те, що в ціль улучило два або більше стрільців). Тоді, згідно з теоремою Бернуллі, р_вр = m/N. У разі значного збільшення числа випробувань N і при будь-якому значенні ε частість враження цілі буде збігатись до ймовірності р_вр = 0,6875.

Приклад 3.Розглянемо більш складну задачу, яку розв'язати аналітично досить важко. Нехай є деяка ціль довільної форми загальною площею S, на яку бомбардувальники скидають п бомб. Площа враження кожної бомби — це круг з радіусом R (рис. 3.2). Ціль вважається враженою, якщо зруйновано К відсотків її площі S. Необхідно знайти ймовірність ураження цілі.

 

 

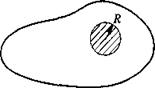
Рисунок 3.2 - Схематичне зображення враження цілі бомбою

Для цього розглянемо область улучення бомб. За допомогою генератора випадкових чисел отримаємо координати падіння п бомб. Біля кожної точки падіння опишемо коло радіусом R (див. рис. 3.3) і визначимо площу враження, яку заштриховано на рисунку. Площу враження можна легко обчислити, використовуючи методи геометрії. Якщо площа враження становить К відсотків (або більше) загальної площі цілі S, то ціль вважається враженою, а випробування — успішним. Інакше ціль вважається неураженою, а випробування — неуспішним.

 

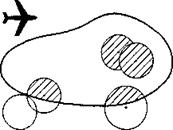
Рисунок 3.3 - Схематичне вирішення задачі

Проведемо N випробувань, моделюючи кожного разу координати п точок падіння бомб, і підрахуємо кількість випробувань, під час яких ціль була враженою. Тоді, згідно з теоремою Бернуллі, ймовірність враження цілі визначається за формулою р_вр = m/Ν, де т — кількість випробувань, за яких ціль була вражена. Оцінку математичного сподівання пло-ші воаження цілі можна визначити як

 

,

 

де S_i — площа враження під час і-го випробування. Згідно із законом великих чисел, якщо N→ ∞, то оцінка буде наближатись до математичного сподівання.

За допомогою методу статистичних випробувань можна обчислити будь-які характеристики випадкових величин і процесів. Крім того, цей метод можна застосовувати для розв'язування не тільки ймовірнісних, а й детермінованих задач. Але під час його застосування слід пам'ятати, що для отримання результату з наперед заданою точністю необхідно провести велику кількість випробувань, для чого потрібні довгі послідовності випадкових чисел.