Випадкова дискретна величина

Одне з основних понять теорії ймовірностей — дискретна випадкова величина X, яка набуває конкретних значень х_i з імовірністю р_i. Ці випадкові величини називають цілочисловими. Якщо можливі значення випадкової величини становлять скінченну послідовність, то розподіл імовірностей випадкової величини визначають, задаючи значення х₁, х₂,..., х„ і відповідних їм імовірностей ρ₁ p₂,..., р_n. Моделювання випадкової дискретної величини виконується аналогічно моделюванню гру­пи несумісних подій, тобто випадкову величину X подають як повну групу подій.

 

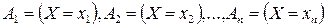
Для моделювання дискретної випадкової величини X зручно використовувати дискретну кумулятивну функцію. Для цього аналізують можливі значення ви­падкової величини X і будують гістограму розподілу можливих значень.

Побудову і використання кумулятивної функції розглянемо на прикладі моде­лювання процесу введення даних під час роботи текстового терміналу. В таблиці 4.1 наведено результати, які відображають результати спостереження за об'ємом інформації, яка вводиться з терміналу під час обробки одного повідомлення.

 

Таблиця 4.1 – Результати спостереження за об’ємом введеної з терміналу інформації

Кількість символів	Розподіл (частка повідомлень зазначеної довжини)	Кумулятивний розподіл (частка повідомлень зазначеної обо меншої дожини)
Менше 6	Відсутній	Відсутній
6 – 10	0,390	0,390
11 – 15	0,214	0,604
16 – 20	0,186	0,790
21 – 25	0,140	0,930
26 – 30	0,007	1,000
Більше 30	Відсутній	1,000

 

На рисунку 4.4 і 4.5 зображено відповідно гістограму та кумулятивну функцію розподілу, наведених у таблиці 4.1.

 

 

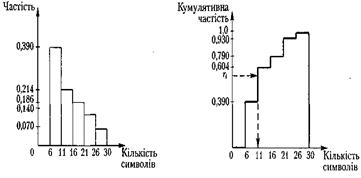
Рисунок 4.4 - Гістограма розподілу Рисунок 4.5 – Кумулятивна функція

довжини повідомлень розподілу довжини повідомлень

 

Слід звернути увагу, що висота кумулятивної функції за заданих значень кіль­кості символів дорівнює сумі значень, наведених на рисунку 4.4. Для того щоб під час імітаційного моделювання роботи терміналу відтворити кількість символів, які вво­дяться з клавіатури, необхідно згенерувати випадкове число з діапазону від 0 до 1 (значення по вертикальній осі), а потім на горизонтальній осі визначити кількість уведених символів, які відповідають цьому числу. Наприклад, якщо випадкове число дорівнює 0,578, (див. рис. 4.5), то кількість символів, уведених з терміналу, можна прийняти таким, що дорівнює 11. Цей підхід ілюструє метод оберненої функ­ції, згідно з яким спочатку генерується випадкове рівномірно розподілене число r_i що задає значення кумулятивної функції розподілу, за яким потім визначається зна­чення аргументу функції х_i = F^-1(r_i), і = 1, 2,..., п, де F'^-1 — обернена до F функція.

На практиці часто застосовують дискретні випадкові величини, що набувають лише невід'ємних значень j = 0,1, 2,..., k,..., n з імовірностями Р₀,Р₁,Р₂, ....,P_k....Р_п, тобто функція розподілу дискретної величини x має вигляд

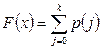(4.2)

У цьому випадку обернену функцію можна записати як

(4.3)

де згідно з умовою .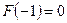

 

4.5 Біноміальний розподіл

Біноміальний розподіл, або розподіл Бернуллі, — це розподіл дискретної випад­кової величини, яка приймає два і тільки два значення: 1 — «true», або «істина», та 0 — «false», або «хибність». Цей розподіл показує ймовірність настання деякої події за n незалежних повторних випробувань, у кожному з яких подія настає з імовірністю р, тобто ймовірність s успішних наслідків у n випробуваннях.

Залежно від значення п можна вибрати один із двох способів моделювання ви­падкової величини з біноміальним розподілом. За невеликих n значення випад­кової біноміально розподіленої величини визначається як кількість чисел у послідовності {r_i} з n чисел, які не перевищують значення р. Припустимо, що потрібно отримати випадкову величину, яка належить біноміальному розподілу з параметрами n = 7 і ρ = 0,3. Для цього спочатку генеруємо послідовність із семи зна­чень r_i. 0,0234; 0,1234; 0,7459; 0,0341; 0,8451; 0,1905; 0,5302, а потім рахуємо ті з них, які менші ніж р. У даному випадку в послідовності тільки чотири значення менші, ніж 0,3. Таким чином, значення випадкової величини, розподіленої за біноміальним законом, дорівнює 4.

За великих значень n і малих ρ можна діяти таким чином. Генеруємо рівномірно розподілені випадкові числа r_i доти, доки не виконається умова

(4.4)

де и₀ та и_j+i задаються виразами

 

Значення випадкової величини з біноміальним розподілом дорівнює кількості випробувань п, які необхідно провести, доки не буде справджуватись умова ( 4.4).

4.6 Розподіл Пуассона

Випадкову величину з розподілом Пуассона можна отримати, якщо припустити, що кількість незалежних випробувань n у біноміальному розподілі прямує до нескінченності, а ймовірність успішного випробування ρ - до нуля, причому добуток пр є незмінним і дорівнює λ. Функція щільності розподілу Пуассона зада­ється виразом

 

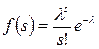
Таким чином, розподіл Пуассона є граничним випадком біноміального та опи­сує випадкові події, які мають місце дуже рідко. На практиці згідно з біноміальним законом розподілені кількість дефектів у готовому виробі та кількість аварій на транспорті за деякий тривалий проміжок часу, кількість дзвінків у телефонній мережі за одиницю часу та ін.

Щоб отримати випадкову величину s з розподілом Пуассона, генеруємо послідовність рівномірно розподілених випадкових чисел r_і і знаходимо їх добуток, перевіряючи нерівність

(4.5)

 

У разі виконання умови (4.5) число п-1 і є випадковою величиною, що належить сукупності, розподіленій за законом Пуассона з математичним сподіванням λ. Якщо умові (4.5) відповідає перше із чисел г_і, то значення випадкової величини s=0.