рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Философия
- /
- Моделювання неперервних випадкових величин
Реферат Курсовая Конспект
Моделювання неперервних випадкових величин
Моделювання неперервних випадкових величин - раздел Философия, Основні поняття системи та моделі. Поняття моделі. Співвідношення між моделлю та системою Існує Кілька Методів Моделювання Значень Неперервних Випадкових Величин З До...
Існує кілька методів моделювання значень неперервних випадкових величин з довільним законом розподілу на основі випадкових чисел, рівномірно розподілених у інтервалі [0, 1]: метод оберненої функції, метод відсіювання, наближені методи тощо.
4.7.1 Метод оберненої функції
Розглянемо метод моделювання випадкової величини, яка має функцію щільності ймовірностей f(x) і монотонно зростаючу функцію розподілу F(х) (рис. 4.9). Суть методу така. За допомогою генератора випадкових чисел генеруємо значення випадкової величини ri·, якому відповідає точка на осі ординат. Значення випадкової величини хi з функцією розподілу F (х) можемо одержати з рівняння F(xi) = ri.
Дійсно, якщо на осі ординат відкласти значення ri випадкової величини, розподіленої рівномірно в інтервалі [0, 1], і на осі абсцис знайти значення хi випадкової величини (рис. 4.6), при якомуF(xi) = ri, то випадкова величина X = F-1 (r) буде мати функцію розподілу F(x).
Таким чином, послідовність випадкових чисел r1, r2, r3, ... перетворюється на послідовність хи х2, х3,..., яка має задану функцію щільності розподілу f(x).

Рисунок 4.6 – Використання методу оберненої функції для генерування неперервної випадкової величини
Звідси випливає загальний алгоритм моделювання випадкових неперервних величин, що мають задану функцію розподілу ймовірностей:
- генерується випадкове число ri є [0, 1];
- обчислюється випадкове число хi яке є розв'язком рівняння

Приклади застосування методу наведені нижче.
4.7.2 Рівномірний розподіл
У загальному випадку випадкова величина X є рівномірно розподіленою на відрізку [а, b], якщо її щільність розподілу ймовірностей має вигляд
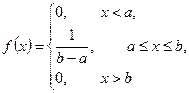
Функцію розподілу ймовірностей можна знайти як

тобто
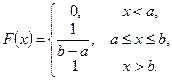
Математичне сподівання та дисперсія випадкової величини X визначаються як
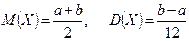
|
Для моделювання випадкової рівномірно розподіленої на відрізку [а, b] величини можна скористатись методом оберненої функції. Обчислимо функцію розподілу випадкової величини та прирівняємо її до значення ri.

|
Звідси знаходимо значення випадкової величини з функцією розподілу f(x):

Цю формулу також можна отримати, якщо виконати лінійне перетворення інтервалу [0,1] у відрізок [а, b]. Для цього потрібно змінити масштаб функції рівномірного розподілу, помноживши її на (b - а), а потім змістити її на величину а.
Функція рівномірного розподілу широко застосовується для моделювання випадкових величин, для яких функція розподілу невідома, а відоме лише її середнє значення. У такому випадку припускають, що відомими є середнє значення випадкової величини та деяке розсіювання (+ -Δ ) її значень відносно середнього. Це дає змогу стверджувати, що дана випадкова величина має рівномірний розподіл.
Прикладами реальних задач, в яких виникає необхідність моделювання рівномірно розподілених випадкових величин, можуть бути аналіз помилок округлення під час проведення числових розрахунків (точність задається як кількість десяткових знаків), час переміщення головок у магнітних накопичувачів (мінімальний та максимальний час), відхилення від розкладу руху транспортних засобів (наприклад, метро).
4.7.3 Експоненціальний розподіл
Експоненціальний закон розподілу набув широкого використання в теорії надійності складних систем. Функція щільності експоненціального розподілу випадкової величини має вигляд
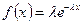
Для її моделювання скористаємося методом оберненої функції. Маємо
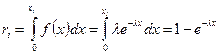 (4.6)
(4.6)
З виразу (4.6) знаходимо значення хi.

Можна показати, що випадкові величини (1 - ri) мають такий самий розподіл, що і величини ri. Тоді, замінивши 1 - ri на ri отримаємо
 .
.
Випадкові величини з експоненціальним розподілом широко застосовуються в задачах моделювання та аналізу СМО, наприклад під час моделювання процесів виходу з ладу та ремонту обладнання, які виникають у складних системах, у разі визначення інтервалів часу між послідовними викликами абонентів у телефонній мережі або замовлень від незалежних клієнтів у будь-якій мережі обслуговування (швидка допомога, служби ремонту, виклик таксі і т. ін.)
4.7.4 Пуассонівський потік
Розглянемо моделювання пуассонівського потоку з інтенсивністю λ, основна властивість якого полягає в тому, що ймовірність надходження k вимог протягом інтервалу довжиною t становить
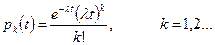
Для пуассонівського потоку інтервали часу між надходженням двох сусідніх вимог мають експоненціальний закон розподілу (див. розділ 2.1). Тому для його моделювання достатньо отримати ряд чисел з таким розподілом. Це можна реалізувати за допомогою методу оберненої функції, якщо ряд випадкових чисел ri рівномірно розподілених у інтервалі [0, 1], перетворити згідно з функцією, оберненою до експоненціальної функції розподілу

де tj — j-й проміжок часу між надходженнями двох сусідніх вимог; Τ = 1/λ — середнє значення проміжку часу між надходженнями двох сусідніх вимог; rj — j-e число в послідовності випадкових чисел з рівномірним розподілом у інтервалі [0, 1].
4.5.5 Нормальний розподіл
Випадкова величина X має нормальний розподіл (розподіл Гаусса), якщо її щільність
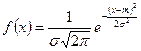
де т — математичне сподівання, а σ — середньоквадратичне відхилення розподілу ймовірностей описується виразом
Функція розподілу нормально розподіленої величини X має вигляд
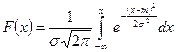
Для моделювання випадкової величини з нормальним законом розподілу безпосередньо скористатися методом оберненої функції не можна, оскільки неможливо аналітично виконати перетворення виду X = F-1(r). Тому для моделювання слід скористатися методом згорток.
Метод згорток базується на центральній граничній теоремі — одному із найбільш видатних результатів теорії ймовірностей: за широких припущень відносно розподілів суми великої кількості взаємно незалежних малих випадкових величин має місце розподіл, який близький до нормального. Метод згорток передбачає зображення випадкової величини як суми незалежних однаково розподілених випадкових величин зі скінченними математичним сподіванням і дисперсією.
Найпростіший метод отримання значення випадкової величини, що має заданий нормальний розподіл, передбачає виконання таких кроків. Спочатку формують послідовність ri (і = 1,n) незалежних, рівномірно розподілених у інтервалі [0, 1] величин і обчислюють суму 12 випадкових чисел, потім віднімають число 6. Величина п= 12 є хорошим наближенням до нормально розподіленої випадкової величини з нульовим математичним сподіванням mz = 0 і одиничним середньоквадратичним відхиленням σζ = 1. Нормальний розподіл з параметрами тг - 0 та σζ = 1 називається стандартним.
Недоліком розглянутих вище методів моделювання є те, що значення функції нормального розподілу, які лежать за межами тх ± σх, суттєво відрізняються від точних значень. Щоб зменшити загальну похибку моделювання, треба використовувати більш точні методи отримання значень функції нормального розподілу. Ці методи базуються на такій властивості. Якщо Xt і Х2 є незалежними нормально розподіленими випадковими величинами з нульовим математичним сподіванням і одиничним середньоквадратичним відхиленням, то величина кута між віссю абсцис і вершиною випадкового вектора з координатами {х, х2) має рівномірний розподіл і не залежить від довжини вектора ( ) ( рис. 4.7).
) ( рис. 4.7).
– Конец работы –
Эта тема принадлежит разделу:
Основні поняття системи та моделі. Поняття моделі. Співвідношення між моделлю та системою
Людина постійно моделює оскільки моделі спрощують об єкти і явища... Величезні можливості мають комп ютери для розв язування математичних задач Числовими методами для більшості задач...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Моделювання неперервних випадкових величин
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов