Характеристики СМО

СМО – це такі системи, в які в випадкові моменти часу поступають заявки на обслуговування, при цьому заявки, які поступили на обслуговування, обслуговуються за допомогою наявних в системі каналів обслуговування.

У будь-якій системі обслуговування передбачена наявність пристроїв для обслуговування (прилади, сервери, канали) і вимог (заявка, виклик, клієнт), які потребують обслуговування. Правила або алгоритми взаємодії пристроїв і вимог називаються дисциплінами поставлення в чергу та обслуговуванням.

З позиції моделювання, процеси формування черги в СМО можна представити наступним чином. Заявка поступає на обслуговування в чергу і приєднується до черги інших заявок, що поступили раніше. Канал обслуговування вибирає заявку з черги для того, щоб приступити до її обслуговування. Після завершення процедури обслуговування канал приступає до обслуговування наступної заявки, якщо така є в блоці очікування. Цикл функціонування СМО подібного роду повторюється багатократно протягом всього періоду роботи системи, що обслуговує. При цьому передбачається, що перехід системи на обслуговування чергової вимоги після завершення обслуговування попередньої вимоги відбувається миттєво, в випадкові моменти часу.

Для кожної СМО задається режим роботи.

Для заявки може бути потрібно кілька обслуговувань одним або кількома пристроями. За допомогою методів теорії МО розв’язують задачі з проектування та експлуатації однотипних елементів обслуговування – н-д, розраховують кількість контрольно-пропускного обладнання, місць для ремонту, ліній зв’язку, одиниць обчислювальної техніки і т.д.

Окремим типом завдань у теорії МО є визначення місць накопичування вимог у СО, н-д, визначення місць на стелажах на складі, кількість пристроїв вводу/виводу і т.д.

Найчастіше ефективність функціонування будь-якої СМО визначається за такими показниками:

1) середня кількість вимог, які система може обслужити за одиницю часу;

2) середній відсоток вимог, які не були обслужені;

3) ймовірність того, що вимогу, яка надійшла до системи, буде прийнято для обслуговування;

4) середній час очікування вимоги в черзі;

5) закон розподілу часу очікування;

6) середня кількість вимог у черзі;

7) закон розподілу числа вимог у черзі;

8) коефіцієнт завантаження пристрою для обслуговування;

9) середня кількість пристроїв, зайнятих обслуговуванням.

Щоб визначити ці компоненти, потрібно охарактеризувати СМО, тобто описати і задати такі основні характеристики:

1) вхідний потік вимог – вимоги, які надходять до СМО на обслуговування;

2) дисципліна черги;

3) механізм обслуговування, правила, за якими здійснюється обслуговування;

4) вихідний потік вимог – вимоги, які залишають систему;

5) режими роботи системи.

5.1.2 Вхідний потік вимог

Для визначення вхідного потоку вимог потрібно зазначити моменти часу надходження вимог до системи (закон надходження) і кількість вимог, які можуть надійти одночасно. Закон надходження може бути детермінованим (н-д, вимога або вимоги надходять до системи у фіксовані моменти часу) або ймовірнісним (проміжки часу між моментами надходження вимог до системи мають рівномірний, експоненціальний або інший заданий закон розподілу).

Вимоги можуть бути одиничні та групові (в систему поступають групами). В останньому випадку мова йде про систему з паралельно-груповим обслуговуванням.

В СМО зустрічаються такі основні типи вхідних потоків, що дозволяють визначити більш прості методи їх опису:

1) регулярним називається потік, в якому задачі поступають в СМО в моменти часу t_i через однакові інтервали часу Δt_i. Для регулярного потоку:

Δt₁ = Δt₂ = …= Δt_n, де Δt_i = const

В обчислювальних системах регулярні потоки зустрічаються рідко але більшість потоків можна подати та розглядати як квазірегулярні з відповідним аналітичним описом;

2) випадковим називається потік, в якому задачі поступають в СМО по черзі в довільні моменти часу. Для випадкового потоку:

Δt₁ ≠ Δt₂ ≠ …≠ Δt_n , де Δt_i = var

3) стаціонарним називається потік, для якого ймовірність виникнення тієї чи іншої кількості задач за визначений інтервал часу τ залежить тільки від тривалості цього інтервалу і не залежить від його розташування на часовій осі.

Ймовірнісний характер стаціонарного потоку в часі є незмінним. Для стаціонарних потоків закон розподілу групи випадкових функцій x(t₁), x(t₂) , … , x(t_n) співпадає з законом розподілу:

x(t₁ + b) – x(t_в), x(t₂ + b) – x(t_в), … , x(t_n + b) – x(t_в),

тобто розподіл випадкових функцій залежить від t₁, t₂, … , t_n і не залежить від величини в, де в – довільний відрізок часу.

4) здебільшого в теорії СМО вважають, що вимоги в систему поступають не групами, а по одній. Ймовірність виникнення кількох одночасних вимог є виключеною або нехтуючи малою. Потік, для якого імовірність P_j(t_i) одночасного поступлення кількох задач j>1 в СМО в довільний момент часу t_i є нехтуючи малою, називається ординарним, тобто:

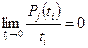
5) властивість відсутності післядії характеризує вхідні потоки, в яких для довільних інтервалів часу число задач, що формується в попередні інтервали ніяким чином не впливає на число задач, що формуються в наступні інтервали, тобто задачі в потоці на обслуговування є повністю взаємонезалежними.

На практиці найбільш часто зустрічаються елементарні потоки, що одночасно володіють властивостями стаціонарності, ординарності та відсутності післядії.

У загальному випадку вхідний потік вимог описується розподілом ймовірностей проміжків часу між моментами надходження до системи двох сусідніх вимог. Якщо ці проміжки часу є незалежними і мають однаковий розподіл випадкових величин, то вимоги утворять стаціонарний вхідний потік.

У класичній теорії МО, як правило, розглядають так званий пуасонівський потік (елементарний), в якому кількість вимог k для будь-якого проміжку часу t має розподіл Пуассона:

, k ≥ 0, t ≥ 0 , (5.1)

Де λ – інтенсивність потоку вимог (кількість вимог, які надійшли до системи за одиницю часу).

5.1.3 Моделювання пуассонівського потоку

Розглянемо найпростіший потік з інтенсивністю λ і позначимо моменти надходження вимог на осі (0,t).

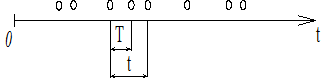
Рисунок 5.1 – Моменти надходження вимог для пуассонівського потоку

Визначимо, який розподіл мають проміжки часу Tміж моментами надходження двох сусідніх вимог.

Очевидно, що проміжки часу Т – випадкові величини. Знайдемо закон їх розподілу. Функція розподілу F(t) визначає ймовірність того, що випадкова величина Т набуде значення, яке менше t, тобто:

F(t)=P, T < t

Нехай t₀ – проміжок часу Т. Знайдемо ймовірність того, що випадкова величина Т буде меншою за t. Для цього потрібно, щоб на проміжок довжиною t, який починається з т. t₀, потрапила хоч одна вимога. Обчислимо функцію F(t) через ймовірність протилежної події, тобто через P₀ того, що за проміжок часу t не надійде жодної вимоги:

F(t) = 1 – P₀

Значення ймовірності P₀ знайдемо за формулою розподілу Пуассона, при умові, що .

(5.2)

Тоді функція розподілу випадкової величини Т має вигляд:

, t > 0 (5.3)

Щоб знайти функцію щільності розподілу f(t) випадкової величини Т, продиференціюємо функцію F(t) за t:

, t > 0 (5.4)

λ = 1; р = 0,5

Отже, щоб отримати пуассонівський потік вхідних вимог, які надходять до системи, достатньо обчислити випадкову величину з експоненціальним розподілом.

Властивості пуассонівського потоку

- стаціонарність;

- відсутність післядії;

- ординарність.

Пуассонівський потік є окремим випадком більш загального потоку Ерланга. Потік Ерланга k-го порядку можна отримати шляхом просіювання пуассонівського потоку, тобто, щоб отримати потік Ерланга k-го порядку треба просумувати k випадкових експоненціально розподілених величин.

Потік Ерланга 1-го порядку (пуассонівський потік)

Потік Ерланга 2-го порядку

Потік Ерланга 3-го порядку

Потік Ерланга 4-го порядку

Рисунок 5.2 – Моделювання потоків Ерланга