Характеристика формальных методов доказательства
Наиболее известными формальными методами доказательства программ являются метод рекурсивной индукции или утверждений Флойда, Наура, метод структурной индукции Хоара и др. [6.4, 6.5, 6.18, 6.19].
Метод Флойда основан на определении условий для входных и выходных данных и в выборе контрольных точек в доказываемой программе так, чтобы путь прохождения по программе пересекал хотя бы одну контрольную точку. Для этих точек формулируются утверждения о состоянии и значениях переменных в них (для циклов эти утверждения должны быть истинными при каждом прохождении циклаинварианта).
Каждая точка рассматривается для индуктивного утверждения того, что формула остается истинной при возвращении в эту точку программы и зависит не только от входных и выходных данных, но и от значений промежуточных переменных. На основе индуктивных утверждений и условий на аргументы создаются утверждения с условиями проверки правильности программы в отдельных ее точках. Для каждого пути программы между двумя точками устанавливается проверка на соответствие условий правильности и определяется истинность этих условий при успешном завершении программы на данных, удовлетворяющих входным условиям.
Формирование таких утверждений - довольно сложная задача, особенно для программ с высокой степенью параллельности и взаимодействия с пользователем. Кроме того, трудно проверить достаточность и правильность самих утверждений.
Доказательство корректности применялось для уже написанных программ и тех, которые разрабатываются методом последовательной декомпозиции задачи на подзадачи, для каждой из них формулируются утверждения с учетом условий ввода и вывода и точек программы, расположенными между входными и выходными утверждениями. Суть доказательства истинности выполнения условий и утверждений относительно заданной программы и составляет основу доказательства ее правильности.
Данный метод доказательства уменьшает число ошибок и время тестирования программы, обеспечивает отработку спецификаций программы на полноту, однозначность и непротиворечивость.
Метод Хоара- это усовершенствованный метод Флойда, основанный на аксиоматическом описании семантики языка программирования исходных программ. Каждая аксиома описывает изменение значений переменных с помощью операторов этого языка. Формализация операторов перехода и вызовов процедур обеспечивается с помощью правил вывода, содержащих индуктивные высказывания для каждой точки и функции исходной программы.
Система правил вывода дополняется механизмом переименования глобальных переменных, условиями на аргументы и результаты, а также на правильность задания данных программы. Оператор перехода трактуется как выход из циклов и аварийных ситуаций.
Описание с помощью системы правил утверждений - громоздкое и отличается неполнотой, поскольку все правила предусмотреть невозможно. Данный метод проверялся экспериментально на множестве программ без применения средств автоматизации из-за их отсутствия.
Метод Маккартисостоит в структурной проверке функций, работающих над структурными типами данных, структур данных и диаграмм перехода во время символьного выполнения программ. Эта техника включает в себя моделирование выполнения кода с использованием символов для изменяемых данных. Тестовая программа имеет входное состояние, данные и условия ее выполнения.
Выполняемая программа рассматривается как серия изменений состояний. Самое последнее состояние программы считается выходным состоянием и если оно получено, то программа считается правильной. Данный метод обеспечивает высокое качество исходного кода.
Метод Дейкстрыпредлагает два подхода к доказательству правильности программ. Первый подход основан на модели вычислений, оперирующей с историями результатов вычислений программы, анализом путей прохождения и правил обработки большого объема информации. Второй подход базируется на формальном исследовании текста программы с помощью предикатов первого порядка. В процессе выполнения программа получает некоторое состояние, которое запоминается для дальнейших сравнений.
Основу метода составляет математическая индукция, абстрактное описание программы и ее вычисление. Математическая индукция применяется при прохождении циклов и рекурсивных процедур, а также необходимых и достаточных условий утверждений. Абстракция позволяет сформулировать некоторые количественные ограничения. При вычислении на основе инвариантных отношений проверяются на правильность границы вычислений и получаемые результаты.
Процесс формального доказательства правильности программ методом математической индукции зарекомендовал себя как система правил статической проверки правильности программ за столом для обнаружения в них формальных ошибок. С помощью этого метода можно доказать истинность некоторого предположения  в зависимости от параметра
в зависимости от параметра  для всех
для всех  , и тем самым доказать случай
, и тем самым доказать случай 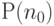 . Исходя из истинности
. Исходя из истинности  для любого значения
для любого значения  , доказывается
, доказывается 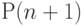 , что достаточно для доказательства истинности
, что достаточно для доказательства истинности  для всех
для всех  .
.
Путь доказательства следующий. Пусть даны описание некоторой правильной программы (ее логики) и утверждение  относительно этой программы, которая при выполнении достигает некоторой определенной точки. Проходя через эту точку
относительно этой программы, которая при выполнении достигает некоторой определенной точки. Проходя через эту точку  раз, можно получить справедливость утверждения
раз, можно получить справедливость утверждения 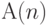 , если индуктивно доказать, что:
, если индуктивно доказать, что:
1.  справедливо при первом проходе через заданную точку,
справедливо при первом проходе через заданную точку,
2. если 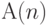 справедливо при
справедливо при  проходах через заданную точку, то справедливо и
проходах через заданную точку, то справедливо и 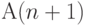 прохождение через заданную точку
прохождение через заданную точку 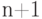 раз.
раз.
Исходя из предположения, что программа в конце концов успешно завершится, утверждение о ее правильности будет справедливым.