Описание алгоритма
Алгоритм, разработанный Ривестом, Шамиром и Адлеманом, использует выражения с экспонентами. Данные шифруются блоками, каждый блок рассматривается как число, меньшее некоторого числа n. Шифрование и дешифрование имеют следующий вид для некоторого незашифрованного блока М и зашифрованного блока С.
С = Ме (mod n)M = Cd (mod n) = (Me)d (mod n) = Med (mod n)Как отправитель, так и получатель должны знать значение n. Отправитель знает значение е, получатель знает значение d. Таким образом, открытый ключ есть KU = {e, n} и закрытый ключ есть KR = {d, n}. При этом должны выполняться следующие условия:
1. Возможность найти значения е, d и n такие, что Med = M mod n для всех М < n.
2. Относительная легкость вычисления Ме и Сd для всех значений М < n.
3. Невозможность определить d, зная е и n.
Сначала рассмотрим первое условие. Нам необходимо выполнение равенства:
Med = М (mod n)Рассмотрим некоторые математические понятия, свойства и теоремы, которые позволят нам определить e, d и n.
1. Если 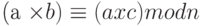 , то
, то  , если а и n взаимнопростые, т.е gcd (a, n) = 1.
, если а и n взаимнопростые, т.е gcd (a, n) = 1.
2. Обозначим Zp - все числа, взаимнопростые с p и меньшие p. Если p - простое, то Zp - это все остатки. Обозначим w-1 такое число, что  .
.
Тогда 
Доказательство этого следует из того, что т.к. w и p взаимнопростые, то при умножении всех элементов Zp на wостатками будут все элементы Zp, возможно, переставленные. Таким образом, хотя бы один остаток будет равен 1.
3. Определим функцию Эйлера следующим образом: 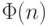 - число положительных чисел, меньших n и взаимнопростых сn. Если p - простое, то
- число положительных чисел, меньших n и взаимнопростых сn. Если p - простое, то 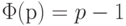 .
.
Если p и q - простые, то  .
.
В этом случае Zp x q ={0, 1, ј, (p x q - 1)}.
Перечислим остатки, которые не являются взаимнопростыми с p x q:
{p, 2 x p, ј, (q-1) x p}{q, 2 x q, ј, (p-1) x q}0Таким образом 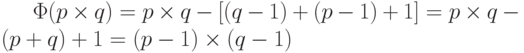 .
.
4. Теорема Ферма.
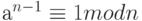 , если n - простое.
, если n - простое.
Если все элементы Zn умножить на а по модулю n, то в результате получим все элементы Zn, быть может, в другом порядке. Рассмотрим следующие числа:
{a mod n, 2 x a mod n, ј, (n-1) x a mod n} являются числами {1, 2, ј, (n-1)}, быть может, в некотором другом порядке. Теперь перемножим по модулю n числа из этих двух множеств.

n и (n-1)! являются взаимнопростыми, если n - простое, следовательно, 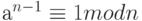 .
.
5. Теорема Эйлера.
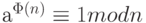 для всех взаимнопростых a и n.
для всех взаимнопростых a и n.
Это верно, если n - простое, т.к. в этом случае  . Рассмотрим множество
. Рассмотрим множество  . Теперь умножим по модулю n каждый элемент этого множества на a. Получим множество
. Теперь умножим по модулю n каждый элемент этого множества на a. Получим множество . Это множество является перестановкой множества R по следующим причинам.
. Это множество является перестановкой множества R по следующим причинам.
Так как а является взаимнопростым с n и xi являются взаимнопростыми с n, то a x xi также являются взаимнопростыми с n. Таким образом, S - это множество целых, меньших n и взаимнопростых с n.
В S нет дублей, т.к. если a x xi mod n = a x xj mod n => xi = xj.
Следовательно, перемножив элементы множеств S и R, получим:




Теперь рассмотрим сам алгоритм RSA. Пусть p и q - простые.
n = p x q.Надо доказать, что 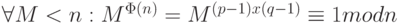
Если gcd (M, n) = 1, то соотношение выполняется. Теперь предположим, что 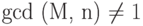 , т.е.
, т.е. 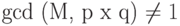 . Пусть
. Пусть 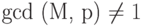 , т.е. M = c x p => gcd (M, q) = 1, так как в противном случаеM = c x p и M = l x q, но по условию M < p x q.
, т.е. M = c x p => gcd (M, q) = 1, так как в противном случаеM = c x p и M = l x q, но по условию M < p x q.
Следовательно,

По определению модуля это означает, что 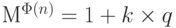 . Умножим обе части равенства на M = c x p. Получим
. Умножим обе части равенства на M = c x p. Получим

Или

Таким образом, следует выбрать e и d такие, что 
Или 
e и d являются взаимнообратными по умножению по модулю 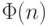 . Заметим, что в соответствии с правилами модульной арифметики, это верно только в том случае, если d (и следовательно, е ) являются взаимнопростыми с
. Заметим, что в соответствии с правилами модульной арифметики, это верно только в том случае, если d (и следовательно, е ) являются взаимнопростыми с 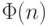 . Таким образом,
. Таким образом, 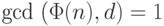 .
.
Теперь рассмотрим все элементы алгоритма RSA.
| p, q - два простых целых числа | - открыто, вычисляемо. |
| n = p x q | - закрыто, вычисляемо. |
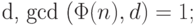
| - открыто, выбираемо. |

| |

| - закрыты, выбираемы. |
Закрытый ключ состоит из {d, n}, открытый ключ состоит из {e, n}. Предположим, что пользователь А опубликовал свойоткрытый ключ, и что пользователь В хочет послать пользователю А сообщение М. Тогда В вычисляет С = Ме (mod n) и передает С. При получении этого зашифрованного текста пользователь А дешифрует вычислением М = С d (mod n).
Суммируем алгоритм RSA:
Создание ключей
| Выбрать простые р и q |
| Вычислить n = p x q |
Выбрать 
|
Вычислить 
|
| Открытый ключ KU = {e, n} |
| Закрытый ключ KR = {d, n} |
Шифрование
| Незашифрованный текст: М < n |
| Зашифрованный текст: С = М е (mod n) |
Дешифрование
| Зашифрованный текст: С |
| Незашифрованный текст: М = Сd (mod n) |
Рассмотрим конкретный пример:
| Выбрать два простых числа: р = 7, q = 17. |
| Вычислить n = p x q = 7 x 17 = 119. |
Вычислить 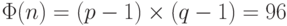 . .
|
Выбрать е так, чтобы е было взаимнопростым с 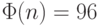 и меньше, чем и меньше, чем  . .
|
Определить d так, чтобы 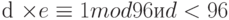 . .
|
| d = 77, так как 77 x 5 = 385 = 4 x 96 + 1. |
| Результирующие ключи открытый KU = {5, 119} и закрытый KR = {77, 119}. |
| Например, требуется зашифровать сообщение М = 19. |
| 195 = 66 (mod 119); С = 66. |
| Для дешифрования вычисляется 6677 (mod 119) = 19. |