Бытия и человеческого мышления

Интересно отметить, что метод последовательных приближений (как и вся вычислительная математика) в классической науке веками считался негативной данью слабости человеческого ума, не способного точно решать абсолютное большинство дифференциальных ура- внений физических теорий. Синергетическая парадигма видит в итерационных процессах типичный нелинейный процесс с обратной связью. И на деле оказалось, что именно в итерационных процессах вычислительной математики самым непосредственным образом проявляют себя подлинно универсальные законы мироздания.

Илл. 33.С фрактальностью ряда геометрических объектов наука столкнулась ещё в XIX в. Самого́ понятия «фрактал» тогда не существовало. Тем более, не существовало тогда и математической теории фракталов, которая стала бурно развиваться только с 1975 г., когда вышла в свет книга Б. Мандельброта «Фрактальная геометрия природы». Осмысление фрактальных объектов в парадигмальном ключе геометрии Евклида и классической теории функций тогда могло лишь фиксировать их парадоксальность. Одним из первых таких парадоксов стала знаменитая задача о длине береговой линии Англии. При повышениях точности измерения приходилось учитывать всё более мелкие дробления береговой линии на бухты и мысы, бухточки и мысочки вплоть до уровня отдельных камешков на кромке воды. В результате длина береговой линии возрастала в огромной степени. Принципиально она была измеримой, но при совершенно нереальных условиях абсолютно спокойных морей по всей береговой линии Англии.

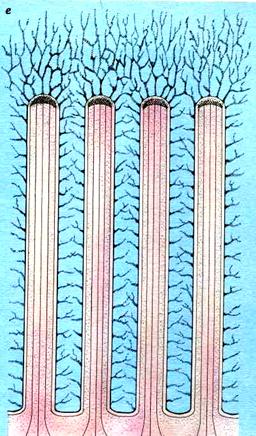
Объекты фактальной геометрии отличаются тем, что их нельзя задать аналитической формулой по типу уравнений окружности, эллипса, конуса, сферы и т. п. Их можно задавать только алгоритмами построения, хотя и не всегда. На рис. 33.1 представлен один из классических фракталов. Он известен с 1906 г. как кривая Коха. Алгоритм его построения прост. На рисунке представлены пять этапов фрактального дробления, которые уже дают представление о самоподобии (скейлинге) фракталов. Три фрагмента кривой Коха со всё бо́льшими увеличениями показаны в трёх окнах сверху. Конечная толщина штриха на рисунках позволяет продемонстрировать эту специфику только так. Но, приложив определённое воображение, можно представить зону присутствия кривой Коха как некую размытую, «туманоподобную» зону конечной ширины. Выбирая в этой зоне какую-то точку, невозможно точно сказать, по какую сторону бесконечно тонкой линии-сердцевины кривой Коха она окажется. Дело в том, что эта бесконечно тонкая и одномерная линия-сердцевина заполняет плоскость в зоне конечной ширины сложнейшим и плотнейшим образом. Здесь можно строить только вероятностные предположения, причём вероятность прямо связана с дробной размерностью кривой Коха, составляющей 1,243… . Эта ситуация вообще является типичной для фрактальных границ раздела. Отметим также, что кривая Коха парадоксальна и с точки зрения классической высшей математики: её одномерная линия-сердцевина является непрерывной кривой, но в то же время ни в одной точке к ней невозможно провести касательную. С точки зрения классического учения о математических функциях, кривая Коха является непрерывной, но недифференцируемой функцией. Теория фракталов снимает этот парадокс тем, что вообще выводит фрактальные объекты за рамки класса непрерывных математических функций и фиксирует их задаваемость только алгоритмами построения.

Кривая Коха относится к классу детерминистских фракталов. Это значит, что у неё есть жёсткий, однозначный алгоритм построения. На илл. 33.2изображён случайный фрактал. Это – знаменитая траектория броуновского движения мельчайшей частицы цветочной пыльцы под влиянием хаотической серии ударов со стороны молекул воды. У броуновской траектории нет однозначного алгоритма построения. В отличие от идеальной кривой Коха, броуновская траектория соответствует реальному физическому процессу. Поэтому шагов её самоподобного дробления «в глубину» всего несколько – в отличие от кривой Коха, которая дробится до бесконечности. С масштаба 10^–6 см начинаются другие структурные уровни организации воды со своими качественно новыми законами, изучаемыми квантовой теорией отдельных атомов и молекул.

Илл. 34.На илл. 34.1 показаны 4 этапа построения другого знаменитого фрактала, известного с 1912 г. Это – ковёр Серпинского. Чёрные квадратные зоны означают вырезания из плоской поверхности исходного квадрата новых и новых частей в духе фрактального дробления. Ковёр Серпинского также является идеальным детерминистским фракталом, поэтому процесс его фрактального дробления также можно продолжать до бесконечности. Но это не значит, что в бесконечном пределе от исходного квадрата останется одна дырка. В итоге получится некая поверхность, которая сильно удалилась от двумерности классических поверхностей, но не приблизилась к одномерности классических линий. Размерность ковра Серпинского 1,893… . Ковёр Серпинского легко обобщить на трёхмерное пространство, получив губку Серпинского с размерностью 2,736… .

Дробная размерность фракталов с вытекающими из неё ключевыми математическими следствиями достаточно очевидна на обыденном уровне. Так, дерево представляет собой геометрический объект с несколькими уровнями фрактального дробления: ствол дробится на ветви, ветви дробятся на ветки, ветки дробятся на сучки; фрактальное дробление продолжается и в жилах листьев. В отличие от идеальных математических фракталов, у дерева это дробление не может быть бесконечным, но оно совершенно чёткое и очевидное. А теперь мысленно поместим дерево как фрактальный геометрический объект в трёхмерную систему декартовых координат, а для сравнения поместим сюда же геометрический объекты из школьной стереометрии – шар и конус. Во втором случае на основе уравнений соответствующих поверхностей легко указать локализацию шара и конуса в пространстве, вычислить объёмы этих фигур. В случае дерева очевидно, что фрактальный объект расположен в пространстве несравненно более сложным и причудливым образом. В этой связи говорят о пространственной делокализации фракталов. Очевидно и то, что вычисление полного объёма, занимаемого стволом, ветвями и т. д. вплоть до мельчайших жилок листьев, для методов евклидовой геометрии является неразрешимой проблемой.

Беря за основу компьютерной графики первоэлементы евклидовой геометрии, невозможно на основе математических алгоритмов построить изображения объектов типа тех растительных форм, которые нас окружают. Максимум, на что способна такая компьютерная графика, – это рисование чертежей деталей машин и самих машин, геометрия которых является сугубо евклидовой. Но если взять за основу математических алгоритмов даже детерминистские фракталы, то с помощью компьютера уже можно строить весьма реалистичные изображения форм растительного царства. На илл. 34.2показано фрактальное формирование изображения листа папоротника. На илл. 34.3 показано фрактальное формирование изображения дерева с раскидистой кроной.

Эти примеры воочию показывают, что в лице геометрии фракталов математика осуществляет гигантский, качественный новый скачок от мира идеальных объектов евклидовой геометрии. Последняя оказалась адекватной миру небесной механики. Процессы космологических масштабов и космические процессы с участием экстремально сильных полей тяготения потребовали перехода к неевклидовой геометрии искривлённых пространств. Фрактальная революция как альтернатива евклидовой геометрии несравненно более радикальна. В её лице математика обретает первооснову из полнокровной геометрии. Благодаря этому она становится способной описывать объективный мир во всём многообразии его геометрических форм. Такая математика немыслима без компьютеров, но компьютеры в науке – это навсегда. Они становятся таким же атрибутом естественно-научного познания, как и научные приборы.

	34.2
		34.3 Илл. 34

Илл. 35.Если даже детерминистские фракталы сами по себе способны формировать реалистичные изображения объектов со сложной геометрией, то это тем более так, когда в соответствующие алгоритмы вводится фактор формообразующей случайности. На илл. 35.1 изображено фрактальное дробление равностороннего треугольника по типу ковра Серпинского. В итоге его внешние контуры не порождают сложных геометрических форм. На илл. 35.2 и 35.3 показан тот же алгоритм фрактального дробления с введением формообразующей случайности: на каждом новом шаге средние линии вписываемых треугольников случайно смещаются от идеального среднего положения. В итоге внешние контуры имитируют нечто подобное очертаниям скалистых гор.

Илл. 36.Книга Б. Мандельброта «Фрактальная геометрия природы» впервые вышла в свет в 1975 г. В настоящее время очевидно, что в развитии науки ХХ в. это было событием, по крайней мере, не менее эпохальным, чем выход в свет в 1948 г. «Кибернетики» Н. Винера. Как это часто бывает в науке, новая парадигма геометрии буквально открыла глаза учёным, позволила им совершенно по-новому увидеть окружающий нас мир природы. Оказывается, фрактальные структуры в мире земной природы окружают нас со всех сторон: явно самоподобные кучевые облака, деревья, древоподобные бассейны рек, сокровенно фрактальные перистые облака, морозные узоры на стекле, скалистые горы и многое другое.

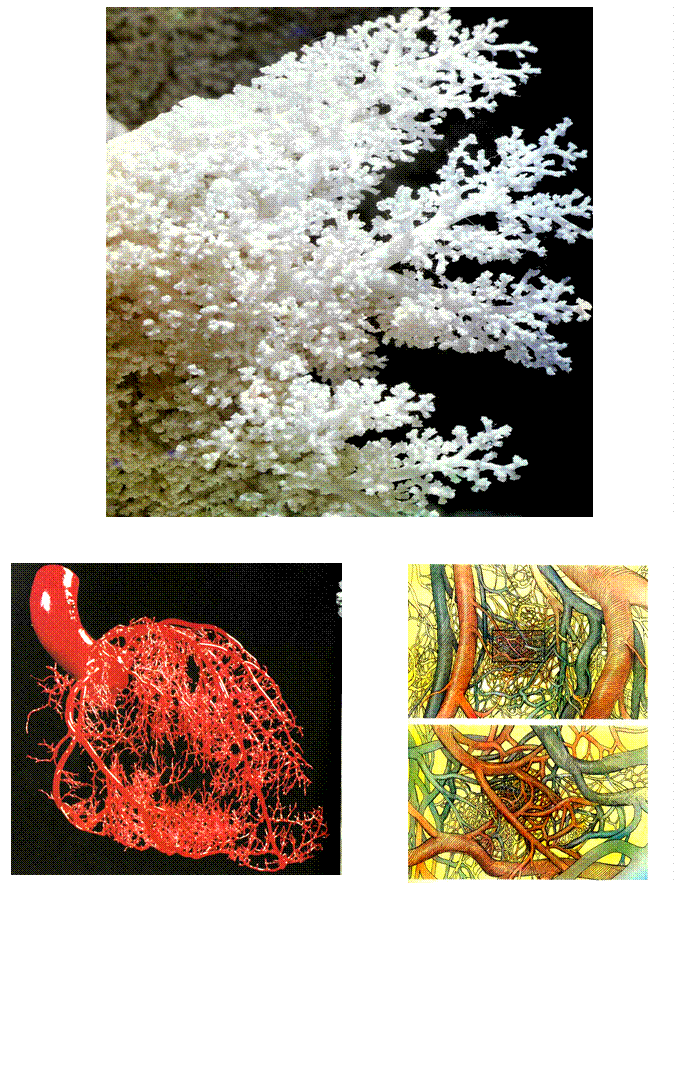
Фрактальное дробление структур широко используется природой в физиологии человека, в строении (морфологии) органов его тела. Физика и химия процессов передачи кровью кислорода тканям, усвоения кислорода лёгкими, усвоения пищи в кишечнике и др. характеризуются медленными темпами течения процессов диффузии, ключевых биохимических реакций и т. п. Этот фактор восполняется фрактальным развитием на много порядков площадей, на которых в тканях и органах осуществляются соответствующие процессы. Илл. 36.1 показывает фрактальную структуру бронхов. Илл. 36.2 показывает фрактальную структуру кровеносных сосудов сердечной мышцы (миокарда), которая нуждается в особо эффективном кровоснабжении. (Кстати, если все большие, средние, малые, мелкие и мельчайшие кровеносные сосуды (капилляры) человеческого тела «расфракталить» и вытянуть в одну линию, то она протянется на тысячи километров.)

В отличие от идеальных математических фракталов, в природных фрактальных структурах такое дробление не может быть бесконечным. Через несколько шагов такого дробления начинаются более глубокие структурные уровни объектов с качественно новыми законами функционирования и строения: ниже структурного уровня тканей – уровень клеток; ниже структурного уровня броуновского движения молекул – уровень процессов квантовой физики атомов и молекул и т. п. Однако то обстоятельство, что в современной математике фрактальные структуры выходят на первые роли, весьма многозначительно: математический язык науки в своей геометрической первооснове становится глубоко родственным геометрии материального мира во всём её реальном многообразии.

Серия илл. 36.3 показывает (слева направо, сверзу вниз) фрактальную структуру стенки кишечника человека. На илл. 36.4. представлена фрактальная изрезанность береговых структур, наблюдаемая с орбиты спутника Земли. Илл. 36.5 демонстрирует древоподобную фрактальную структуру мощной линейной молнии. Илл. 36.6 представляет фрактальное дробление горных структур, видимое из космоса. Левая илл. 36.7 представляет фрактальность бассейнов горных рек, также очевидную с околоземной орбиты. Правая илл. 36.7 представляет вид из космоса на устье реки Миссисипи в США. Поистине, фрактальная геометрия – это геометрия реальной природы, окружающей нас со всех сторон!