Лекція 13

Оптимізація параметрів для математичних моделей динаміки популяції

 

Логістична модель є значним розширенням експоненціального закону. Але вона теж має певні рамки застосування. Нехай логістична модель (12.17) описує розмноження популяції риб в озері. Якщо на кількість риби впливають тільки природні фактори, то за певних сприятливих природних умов чисельність риби можна спрогнозувати за допомогою моделі (12.17). Але, якщо в розвиток риб втрутилась людина, наприклад, якщо щорічно виловлюється q одиниць риби, то замість моделі (12.17) потрібно розглянути модель:

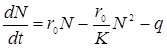(13.1)

За допомогою заміни змінних

(13.2)

рівняння (13.2) приведемо до простішого вигляду:

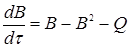(13.3)

Модель популяції риб (34) описує динаміку чисельності риб у нових умовах, коли починає діяти антропогенний фактор. Дослідимо рівняння (13.3) та побудуємо графік зміни швидкості розмноження і графік динаміки популяції риб у нових умовах при різних значеннях інтенсивності вилову риби Q.

Стаціонарний режим (він же й оптимальний) визначається з умови рівності 0 правої частини (13.3):

. (13.4)

Знайдемо корені квадратного рівняння:

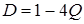
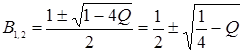(13.5)

Залежно від значень Q матимемо різні корені рівняння (13.5).

1) Якщо Q=1/4, то D=0 і рівняння (13.3) має один корінь В=1/2. Побудуємо графіки згідно рівняння (13.5) при Q=1/4.

 

Аналіз рис.13.1 дозволяє зробити висновок, що для даного випадку точка В=1/2 – стаціонарна. Похідна функції B(t) від’ємна при всіх B>0. Отже функція B(t) повинна бути спадною при всіх B>0, тому графік залежності чисельності популяції риби від часу набуде вигляду.

Аналізуючи рис.13.2 можна зробити висновок, що значення інтенсивності вилову риби Q=1/4 приводить до одного стаціонарного режиму: буде-яке початкове значення чисельності популяції з часом виходить на стаціонарний режим В=1/2. Але цей стаціонарний режим є нестійким: невелике випадкове зменшення чисельності B<1/2 приводиться до повного знищення популяції за обмежений відрізок часу.

2. При великому вилові риби Q>1/4 підкореневий вираз (13.5) від’ємний, отже розв’язків (13.4) не має і відповідно стаціонарний режим не можливий. Графік залежності швидкості розмноження від чисельності популяції матиме вигляд (рис.13.3).

Аналіз рис.13.3 дозволяє зробити висновок, що для даного випадку похідна функції B(t) від’ємна при всіх B>0. Отже функція B(t) повинна бути спадною при всіх B>0, тому графік залежності чисельності популяції риби від часу набуде вигляду (рис.13.4).

 

Отже, при інтенсивності вилову риби Q>1/4 популяція знищується за певний проміжок часу, якою б великою вона не була в початковий момент часу.

3. При малій інтенсивності вилову будемо мати два корені рівняння (13.4) – В₁ і В₂ і відповідно два стаціонарні режими. Побудуємо графіки згідно рівняння (13.3).

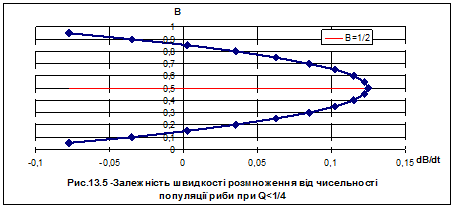
Аналіз рис.13.5 дозволяє зробити висновок, що для даного випадку похідна функції B(t) від’ємна при B<B₁ і В>B₂ і додатна при 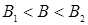. Отже функція B(t) повинна бути спадною при B<B₁ і В>B₂ і зростаючою при 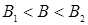, тому графік залежності чисельності популяції риби від часу набуде вигляду (рис.13.6).

 

Таким чином, при чисельності популяції B<B₁ популяція з часом знищується повністю, при 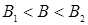чисельність популяції з часом збільшується і виходить на стаціонарний режим В₂, при В>B₂ чисельність популяції з часом зменшується і виходить на стаціонарний режим В₁.

Таким чином, планування вилову риби приводить до повного знищення жорстко регульованої системи внаслідок виникнення нестійких режимів, що з’являються при оптимізації. Замінимо «жорстке» планування вилову «м’яким», що враховує зворотній зв’язок, тобто величина вилову залежить від чисельності популяції. Нехай ця залежність має такий вигляд:

 

(13.6)

 

де параметр (диференційована квота) підлягає вибору.

У даному разі модель (13.3) набуває вигляду:

(13.7)

Стаціонарний режим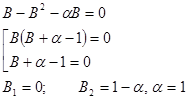

При режим буде стійким, оскільки . При 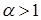– нестійкий, оскільки .

 

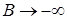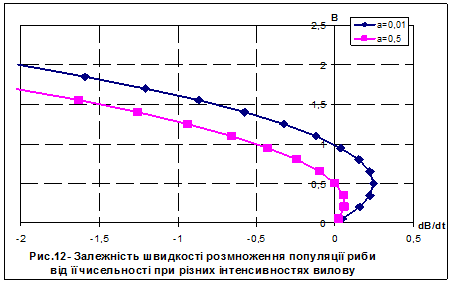
За графіком рис. 13.7 видно, що похідна функції В(t) від’ємна при 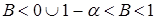, отже на цих проміжках функція буде спадною. При 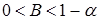похідна функції В(t) додатня, відповідно функція зростаюча.

Виходячи з даного аналізу побудуємо залежність чисельності популяції від часу (рис.13.8).

 

Таким чином інтенсивність вилову при стаціонарному режимі .

Знайдемо величину значення параметра при максимальному вилові риби. Для цього прирівняємо до нуля похідну інтенсивності вилову:

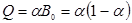.(13.8)

 

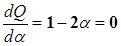(13.9)