Теорема Чебышева и следствия из нее

В теореме Чебышева доказывается, какие условия должны выполняться для тригонометрического полинома наилучшего приближения.

Теорема Чебышева. Для того чтобы тригонометрический полином был полиномом наилучшего равномерного приближения непрерывной функции 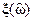на интервале 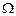, необходимо и достаточно, чтобы максимум модуля взвешенной ошибки аппроксимации достигался в 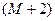точках на интервале 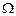, и значения максимальной ошибки последовательно чередовались по знаку.

Следствия из теоремы Чебышева:

1. Полином наилучшего приближения определяется среди полиномов одинакового порядка .

2. Существует единственный полином наилучшего приближения порядка , который обеспечивает

3. Существует единственный полином наилучшего приближения, который при заданной максимальной ошибке аппроксимации обеспечивает

4. Точки, в которых модуль ошибки аппроксимации достигает своего максимума, называют точками альтернанса. Их количество равно:

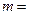(9.7)

5. При решении оптимизационной задачи в (9.6) — определении вектора 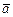— модуль заменяется на

Теорему Чебышева называют теоремой об альтернансе —

Вектор 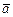определяется с помощью алгоритма Ремеза (см. в книге).