Преобразование колебаний в параметрических и нелинейных цепях
В системах электрической связи применяются различные преобразования сигналов. Одним из важнейших преобразований является модуляция – изменение параметров несущей (переносчика сообщений) по закону первичного сигнала. Проходя от модулятора передатчика до детектора (демодулятора) приемника, сигнал u(t) (см. рис. 1.2) подвергается различным преобразованиям и превращается в сигнал z(t)=s(u, t)+n(t). Преобразование сигналов в модуляторе и детекторе связано с трансформацией спектра входного сигнала, т. е. появлением в выходном сигнале частотных составляющих которых не было на входе.
 Линейные системы с постоянными параметрами (стационарные) не могут трансформировать спектр входного сигнала. Для трансформации спектра можно использовать или линейную систему с переменными параметрами – параметрическую,или нелинейную систему. Ограничимся анализом параметрической системы нулевого порядка (без реактивных элементов) и нелинейной системой нулевого порядка.
Линейные системы с постоянными параметрами (стационарные) не могут трансформировать спектр входного сигнала. Для трансформации спектра можно использовать или линейную систему с переменными параметрами – параметрическую,или нелинейную систему. Ограничимся анализом параметрической системы нулевого порядка (без реактивных элементов) и нелинейной системой нулевого порядка.
 Пусть входное напряжение параметрической системы (рис. 3.1) меняется по гармоническому закону u1(t)=U1·cos(ω1t+φ1), а параметрическая проводимость (крутизна характеристики) меняется по гармоническому закону с частотой управления fу:
Пусть входное напряжение параметрической системы (рис. 3.1) меняется по гармоническому закону u1(t)=U1·cos(ω1t+φ1), а параметрическая проводимость (крутизна характеристики) меняется по гармоническому закону с частотой управления fу:
s(t)=S0+S1·cos(ωуt+φу).
По закону Ома ток в цепи (рис. 3.1) будет равен:
i(t)= u1(t)· s(t)=U1· S0·cos(ω1t+φ1)+ U1·S1·cos(ω1t+φ1)· cos(ωуt+φу). (3.1)
Воспользовавшись известной из тригонометрии формулой cosα·cosβ=0,5·cos(α+β)+ 0,5·cos(α-β), получаем:
i(t)=U1· S0·cos(ω1t+φ1)+0,5·U1·S1·cos[(ω1+ωу)·t+φ1+φу]+ 0,5·U1·S1·cos[(ω1-ωу)·t+φ1-φу]. (3.2)
Таким образом, выходной сигнал (ток) содержит компоненты на частотах ω1+ωу, которых нет во входном сигнале, т. е. произошла трансформация спектра входного сигнала. Необходимые (полезные для решения тех или иных задач) частотные составляющие тока i(t) выделяются с помощью линейной фильтрации.

 На практике параметрический резистивный элемент R(t) получают путем внешнего управления нелинейным сопротивлением. Рассмотрим нелинейный резистивный двухполюсник с вольтамперной характеристикой (ВАХ) i=f(u), на который действуют два напряжения: сигнала u1(t) и управления u2(t) (рис.3.2). Ток в цепи определим как i=f(u1+ u2). Предположим, что сигнал управления существенно превышает входной сигнал, т. е. |u2| >> |u1|. Разлагая ток в ряд Тейлора по малому сигналу u1 и удерживая два члена ряда, получим:
На практике параметрический резистивный элемент R(t) получают путем внешнего управления нелинейным сопротивлением. Рассмотрим нелинейный резистивный двухполюсник с вольтамперной характеристикой (ВАХ) i=f(u), на который действуют два напряжения: сигнала u1(t) и управления u2(t) (рис.3.2). Ток в цепи определим как i=f(u1+ u2). Предположим, что сигнал управления существенно превышает входной сигнал, т. е. |u2| >> |u1|. Разлагая ток в ряд Тейлора по малому сигналу u1 и удерживая два члена ряда, получим:
 |
(3.3)
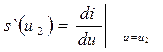 |
Обозначим через - дифференциальная крутизнанелинейного резистора в точке u= u2. Тогда сигнальная составляющая тока будет равна:
 ic(t) = s`[u2(t)]u1(t). (3.4)
ic(t) = s`[u2(t)]u1(t). (3.4)
Следовательно, таким образом можно реализовать цепь с параметрическим сопротивлением R`(u2)=1/s`u2(t). Аналогично можно реализовать цепь с параметрической емкостью и параметрической индуктивностью [1, с. 84].
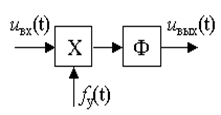
 Согнасно выражению (3.4) параметрический резистивный (безынерционный) элемент можно представить как перемножитель входного uвх(t) и управляющего fу(t), как показано на рис. 3.3.
Согнасно выражению (3.4) параметрический резистивный (безынерционный) элемент можно представить как перемножитель входного uвх(t) и управляющего fу(t), как показано на рис. 3.3.
Вольтамперную характеристику нелинейного сопротивления R(i) очень часто аппроксимируют (относительно рабочей точки, определяемой напряжением смещения Е) (см. рис. 3.4) в общем случае полиномом n-й степени (полиномиальная аппроксимация)
i=a0+a1(u-E)+a2(u-E)2+a3(u-E)3+…+an(u-E)n . (3.5)
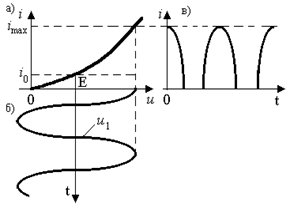 Чем выше степень полинома, тем точнее можно описать ВАХ i=f(u). При малых переменных входных напряжениях можно ограничиться квадратичной аппроксимацией. Необходимо отметить, что если входное переменное напряжение настолько мало, что можно i ограничить линейной аппроксимацией, т. е. i = a0+a1(u-E), то трансформация спектра входного сигнала невозможна. Предоложим, что u = E+u1=E + U1·cos(ω1t+φ1) (см. рис. 3.4,б). Тогда, воспользовавшись формулами кратного аргумента cos2a=(1+cos2a)/2; cos3a=(3соsa+cos3a)/4; cos4a=(3+4cos2a+cos4a)/8 и т. д., получим для тока i:
Чем выше степень полинома, тем точнее можно описать ВАХ i=f(u). При малых переменных входных напряжениях можно ограничиться квадратичной аппроксимацией. Необходимо отметить, что если входное переменное напряжение настолько мало, что можно i ограничить линейной аппроксимацией, т. е. i = a0+a1(u-E), то трансформация спектра входного сигнала невозможна. Предоложим, что u = E+u1=E + U1·cos(ω1t+φ1) (см. рис. 3.4,б). Тогда, воспользовавшись формулами кратного аргумента cos2a=(1+cos2a)/2; cos3a=(3соsa+cos3a)/4; cos4a=(3+4cos2a+cos4a)/8 и т. д., получим для тока i:
 i=I0+I1cos(ω1t+φ1)+I2cos(2ω1t+2φ1)+I3cos(3ω1t+3φ1)+… (3.6)
i=I0+I1cos(ω1t+φ1)+I2cos(2ω1t+2φ1)+I3cos(3ω1t+3φ1)+… (3.6)
здесь  - постоянная составляющая тока;
- постоянная составляющая тока;
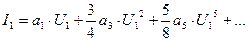 - амплитуда 1-й гармоники;
- амплитуда 1-й гармоники;
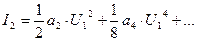 - амплитуда 2-й гармоники;
- амплитуда 2-й гармоники;
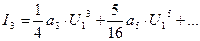 - амплитуда 3-й гармоники и т. д.
- амплитуда 3-й гармоники и т. д.
При бигармоническом воздействии, т. е. если u=E+u1+u2=E+U1·cos(ω1t+φ1)+U2·cos(ω2t+φ2) в составе тока i получаются колебания с комбинационными частотами [1].
Очень часто при исследовании схем с нелинейными элементами при гармонических воздействиях с большими амплитудами ВАХ нелинейного элемента аппроксимируют отрезками прямых линий –кусочнолинейная аппроксимация(КЛА) – см. рис. 3.5.
Зависимость i=f(u) в этом случае можно записать так
 0 при u < Vотс,
0 при u < Vотс,
i = (3.7)
s(u - Vотс) при u Ê Vотс .
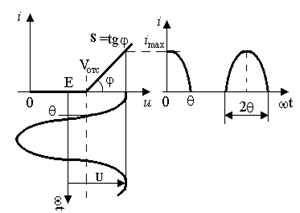 где u=E+Ucosωt , Е – напряжение смещения, определяющее рабочую точку; Vотс – напряжение отсечки.
где u=E+Ucosωt , Е – напряжение смещения, определяющее рабочую точку; Vотс – напряжение отсечки.
График тока i имеет вид косинусоидальных импульсов с углом отсечки Q, определяемым из - выражения
cos Q = (Vотс-E)/U. (3.8)
Угол отсечки может принимать значения от нуля (ток не проходит) до p (линейный режим работы схемы). При E=Vотс, Q=p/2 (проходят положительные полуволны входного сигнала).
 Постоянная составляющая тока i определяется по формуле
Постоянная составляющая тока i определяется по формуле  .
.
Вводя безразмерную переменную х=ωt , получим
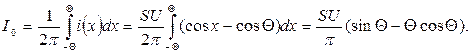
Вводя коэффициент 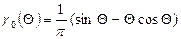 , который называется коэффициентом Берга [1] для постоянной составляющей, можно написать:
, который называется коэффициентом Берга [1] для постоянной составляющей, можно написать:
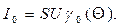 (3.9)
(3.9)
С учетом (3.7) и (3.8) получаем формулу для определения максимального значения тока:
imax= S(E-U-Vотс)= SU(1-cosQ) (3.10)
Tогда I0= imaxa0(Q), (3.11)
где a0(Q)= .
.
Если в ходе исследований фиксируются величины U, S и Q, то для расчетов используется формула (3.9); если фиксируются imax и Q - используется (3.11).
Аналогично находим амплитуду 1-й гармоники тока:
 , (3.12)
, (3.12)
где 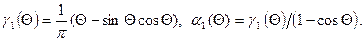
Для n-ой гармоники тока имеем:
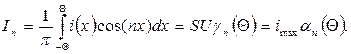 , (3.13)
, (3.13)
где 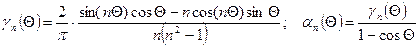 - коэффициенты Берга для n-й гармоники (n=2, 3, … ).
- коэффициенты Берга для n-й гармоники (n=2, 3, … ).
Для часто используемого режима Q=p/2 имеем g0(p/2)=a0(p/2)=1/p, g1(p/2)=a1(p/2)=1/2.