Разложение сигналов в обобщенный ряд Фурье
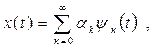 Среди различных математических приемов, используемых при исследовании электрических цепей и сигналов наиболее широко применяется представление произвольной функции х(t) в виде суммы простых (элементарных) функций ΨК(t), так называемых базисными:
Среди различных математических приемов, используемых при исследовании электрических цепей и сигналов наиболее широко применяется представление произвольной функции х(t) в виде суммы простых (элементарных) функций ΨК(t), так называемых базисными:
(2.1)
где αк – коэффициенты разложения. Представление (2.1) называют обобщенным рядом Фурье.
Такой подход лежит в основе принципа наложения (суперпозиции) при изучении линейных электрических цепей. Выбор системы базисных функций Ψk (t) зависит от вида сигнала и решаемой задачи.
Спектральное представление периодических колебаний (сигналов).При формировании и обработке сигналов часто приходится иметь дело с периодическими колебаниями сложной формы. Периодическую функцию х(t)= х(t+nT), Т – период можно представить разложением в обобщенный ряд Фурье по базисным функциям:
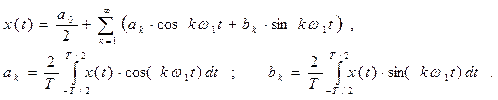 (2.2)
(2.2)
(2.3)
 Представление (2.2) называют просто рядом Фурье. Ряд (2.2) можно записать в виде:
Представление (2.2) называют просто рядом Фурье. Ряд (2.2) можно записать в виде:
(2.4)
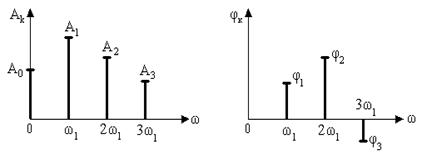
Согласно формуле (2.4) периодическую функцию х(t) можно представить суммой гармонических колебаний с частотами, кратными основной частоте ω1=2π/Т, с амплитудами Аk и начальными фазами Ψk . Совокупность амплитуд Аk образует линейчатый амплитудный спектрсигнала (рис. 2.1, а), а совокупность начальных фаз Ψk - фазовый спектрсигнала (рис. 2.1, б).
Ряд Фурье часто представляют в комплексной форме:
 (2.5)
(2.5)
где Сk - комплексная амплитуда k-той гармоники, определяется по формуле:
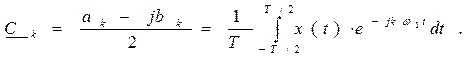 |
(2.6)
Комплексное представление ряда Фурье оказывается удобным при выполнении различных расчетов.
Спектральное представление непериодических сигналов.Разложение в тригонометрический ряд Фурье (2.5) может быть обобщено на случай непериодических сигналов х(t) путем устремления Т→∞ или f = (1/T) → 0.
а - амплитудный спектр б - фазовый спектрПри таком предельном переходе
Рис. 2.1. Спектральное представление периодического сигнала частота ω1=2π∕Т стремится к нулю, бес-
 конечно увеличивается число спектральных составляющих и дискретный линейчатый спектр переходит в сплошной. Для определения этого спектра наиболее удобна комплексная форма ряда Фурье (2.5), но в нем вместо суммы будет интеграл с бесконечными пределами. Тогда формулы (2.5) и (2.6) надо записать в виде:
конечно увеличивается число спектральных составляющих и дискретный линейчатый спектр переходит в сплошной. Для определения этого спектра наиболее удобна комплексная форма ряда Фурье (2.5), но в нем вместо суммы будет интеграл с бесконечными пределами. Тогда формулы (2.5) и (2.6) надо записать в виде:
 (2.7)
(2.7)
где (2.8)
 Формулы (2.7) и (2.8) называются соответственно обратными прямым преобразованиями Фурье (пара преобразований Фурье). Они показывают фундаментальную связь между непериодическим сигналом х(t) и его спектральной плотностью F(ω).Модуль F(ω) определяет сплошной амплитудный спектр непериодического сигнала, а аргумент Ψ(ω) – сплошной фазовый спектр, т. е. F(ω)= F(ω)е-jΨ(ω) . Cтрого говоря, спектральная плотность (2.8) существует для функций х(t), удовлетворяющих условию абсолютной интегрируемости, т. е.
Формулы (2.7) и (2.8) называются соответственно обратными прямым преобразованиями Фурье (пара преобразований Фурье). Они показывают фундаментальную связь между непериодическим сигналом х(t) и его спектральной плотностью F(ω).Модуль F(ω) определяет сплошной амплитудный спектр непериодического сигнала, а аргумент Ψ(ω) – сплошной фазовый спектр, т. е. F(ω)= F(ω)е-jΨ(ω) . Cтрого говоря, спектральная плотность (2.8) существует для функций х(t), удовлетворяющих условию абсолютной интегрируемости, т. е.
- имеет конечное значение.
Свойства комплексной спектральной плотности приведены в [2, с. 34, табл. 2.2]. Значения спектральной плотности для большинства используемых в настоящее время сигналов приведены в математических справочниках и специальной литературе по теории сигналов и цепей, а также в [1, с. 43, табл. 2.1].