Случайные процессы и их основные характеристики

В основе большинства методов исследования общей теории связи лежит представление о процессе передачи сообщения как о случайном процессе,т. е. предопределить заранее точное протекание процесса невозможно. Случайнасть процесса X(t) проявляется в том, что вид наблюдаемой функции случайным образом меняется от одного наблюдения к другому. Однако получаемая в результате каждого отдельного опыта функция х(t) не случайна. Ее называют реализацией случайной функции. Совокупность всех возможных реализаций {х⁽ⁿ⁾(t)} и образует случайный процесс X(t)= {хⁿ(t)}. Для непрерывного случайного процесса число реализаций образует несчетное множество. Но можно установить некоторые закономерности, по которым можно судить о том, что в данном случае случайная величина с вероятностью Р будет принимать значение в пределах [x, x+Δx].

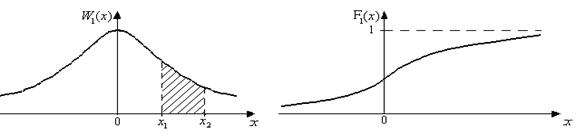
а – одномерная ПВ б – одномерная ИФР

Рис. 2.2. Типовой график

Плотность вероятности(ПВ) иинтегральная функция распределения(ИФР). Для непрерывных

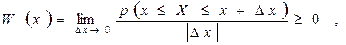случайных процессов X(t) распределение вероятностей в заданном сечении t₁ характеризуется одномерной ПВ

 

(2.14)

выражающей отношение вероятности того, что случайная величина X(t) примет значения в интервале

х ≤ Х ≤ х+Δх, к величине интервала Δх. На рис. 2.2, а изображен типовой график одномерной ПВ.

Вероятность того, что случайная величина Х примет значение в интервале (х₁; х₂):

 

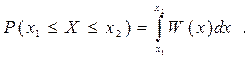(2.15)

Условие нормировки для достоверного события – это величина:

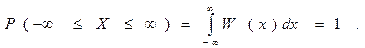(2.16)

 

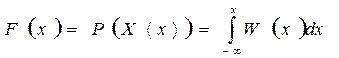Другой важной характеристикой случайных величин является ИФР F(x), определяемая как вероятность того, что случайная величина X не превзойдет некоторого значения х:

 

. (2.17)

 

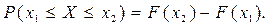График F(x) показан на рис. 2.2, б. ИФР имеет следующие свойства:

1) F(-∞)=0; 2) F(∞)=1; 3) F(x) – неубывающая функция; 4)

Для более полного описания случайного процесса необходимо иметь его n-мерную ПВ или n-мерную ИФР. Нахождение n-мерной ПВ, как и n-мерной ИФР – трудная задача, которую не всегда удается решить.

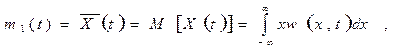Числовые характеристики. На практике часто ограничиваются рассмотрением более простых характеристик случайных величин (процессов), называемых числовыми характеристиками или моментами. Так, момент первого порядка, называемый математическим ожиданием(МО) определяет среднее среднее значение случайной величины как

 

(2.18)

 

где черта сверху означает усредненние по множеству реализаций.

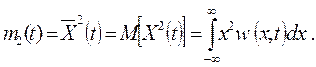Аналогично вводится момент второго порядка

 

(2.19)

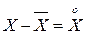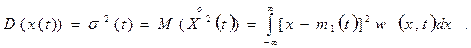Разность между случайной величиной (СВ) Х и ее МО, т. е. представляет собой отклонение СВ от среднего значения. Она называется центрированным значением СВ. МО квадрата этого отклонения называется дисперсией или центральным моментом второго порядка

 

(2.20)

Величину σ = 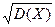называют стандартным или среднеквадратическим отклонением. С учетом (2.18) и (2.19) выражение (2.20) приводится к виду

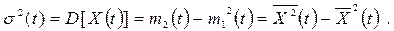(2.21)

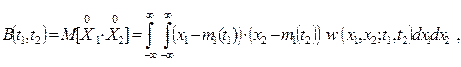Дисперсия характеризует разброс случайной величины относительно ее среднего значения. МО m₁ и дисперсия σ² являются важными характеристиками, но они не дают достаточного представления об изменении случайного процесса во времени. Для этого вводится понятие смешанного момента второго порядка, называемого функцией корреляции:

 

 

(2.22)

где w(х₁, х₂; t₁, t₂) – двумерная ПВ.

Функция корреляции (ФК) характеризует степень статистической взаимосязи значений Х₁ и Х₂ случайного процесса Х(t) в моменты времени t₁ и t₂, разделенные интервалом τ = t₂ - t₁. Убывание ФК с увеличением τ свидетельствует об ослаблении связи между мгновенными значениями процесса. Если ФК при каких-либо значениях τ имеет отрицательное значение, это означает, что положительным отклонениям процесса в одном сечении соответствуют преимущественно отрицательные отклонения в другом сечении и наоборот. Если случайные величины Х₁ и Х₂ статистически независимы, то их двумерные ПВ определяются произведением одномерных ПВ; ФК между двумя такими сечениями равна нулю. МО центрированной СВ всегда равно нулю.

Примеры типовых ПВ и ИФР непрерывных и дискретных СВ приведены в [1, с. 52-56]. Там же рассмотрены стационарные случайные процессы, эргодические процессы и функция корреляции случайного процесса с ограниченным спектром (белого и квазибелого шума).

Некоторые модели источников (сообщений, сигналов, помех) рассмотрены в [1, с. 73 – 78, §2.8]. В последние годы все большее распространение находят модели речевых сигналов в виде динамических порождающих систем. Например, выбирая в качестве динамической системы последовательно соединенные RC-фильтры нижних и верхних частот, получают описание речевого сигнала двухкомпонентным марковским процессом. В этом случае спектральная плотность представляется системой стохастических уравнений состояния. Экспериментальные данные показывают, что если исключить паузы длительностью свыше 350 мс, то одномерная плотность речевого сигнала хорошо аппроксимируется двусторонним гамма-распределением [1].