Попытки доказательства V постулата

Уровень строгости евклидовых доказательств до XIX в. считался вполне достаточным. Необходимость пополне­ния списка его постулатов и аксиом видело лишь небольшое число геометров. Подавляющее большинство сочинений по обоснованию геометрии, напротив, имело целью свести до минимума число евклидовых аксиом и постулатов. На этом пути пристальное внимание многих привлек V постулат Евкли­да. Математики в течение более двух тысяч лет пытались доказать V постулат, как теорему. Еще комментаторы древности считали V по­стулат недоказанной теоремой и старались ис­править «ошибку» Евклида, поместившего его в число недоказуемых предложений.

Это объясняется, види­мо, следующими двумя причинами. Во-первых, V постулат более сложен и непосредственно ме­нее очевиден, чем остальные, так как содержит идею бесконечного. Во-вторых, сам Евклид ис­пользует его в первой книге «Начал» лишь при доказательстве двадцать девятого предложения, тогда как пер­вые двадцать восемь предложений доказаны без его участия.

Нет ни одного крупно­го геометра от Евклида до Лобачевского (XIX в.), который не занимался бы проблемой V постулата. Все эти доказательства, как бы искус­но ни велись были ошибочными, причем содержали логическую ошибку одного плана: доказательство этого посту­лата основывалось на утверждении, которое казалось наглядно очевидным, а вместе с тем было равносильным V постулату. Таких равносильных данному постулату утверждений (эквива­лентов) накопилось много.

Оказалось, что V постулат недоказуем при помощи остальных аксиом евклидовой геомет­рии. Первым, кто показал (но еще не доказал) недоказуемость V постулата, был наш соотечественник, великий геометр Н. И. Лобачев­ский. Он рассуждал примерно так: если V по­стулат не доказывается, то, отрицая его, с по­мощью остальных аксиом «Начал» Евклида, высказанных явно или неявно, никогда не при­дем к противоречию. Таким образом, на базе только что указанной аксиоматики возможна другая геометрия, геометрия в неевклидовом смысле. И Лобачевский построил эту геометрию, которая в честь ее создателя стала называться геометрией Лобачевского. Вполне строго доказал недоказуемость V посту­лата немецкий ученый лауреат премии имени Н. И. Лобачевского Д. Гильберт (1862 - 1943).

Но труд ученых, стремившихся доказать не­доказуемое, не пропал даром. Своей работой они расчистили путь к новой геометрии и взрыхлили почву для прорастания ее идей. Хотя V постулат и не был доказан, но зато были четко выделены аксиомы и теоремы, не зависящие от него. Они-то и составили так называемую абсолютную гео­метрию, первые теоремы которой в чистом виде были даны еще в первой книге «Начал» Евклида (первые 23 теоремы были доказаны Евклидом без помощи V постулата).

Ниже приводим список основных теорем аб­солютной геометрии на плоскости.

1. Любой отрезок (угол) можно единствен­ным образом разделить пополам.

2. Из каждой точки, взятой вне прямой, можно опустить на эту прямую перпендикуляр, и притом единственный.

3. Из каждой точки прямой можно восста­вить перпендикуляр к этой прямой, и притом единственный.

4. Сумма смежных двух углов равняется двум прямым.

5. Вертикальные углы равны.

6. В равнобедренном треугольнике углы при основании равны.

7. Имеют место известные теоремы о срав­нении перпендикуляров, наклонных и их проек­ций, в частности, что перпендикуляр короче на­клонной.

8. Внешний угол треугольника всегда боль­ше любого внутреннего, с ним не смежного.

9. Во всяком треугольнике не может быть больше одного прямого или тупого угла.

10. В каждом треугольнике против большей стороны лежит и больший угол и наоборот.

11. В любом прямоугольном треугольнике гипотенуза больше любого из катетов.

12. Сумма любых двух сторон треугольника всегда больше третьей.

13. Если две прямые, будучи пересечены третьей, образуют с ней равные соответственные углы, или равные накрестлежащие углы, или сумму односторонних углов, равную 2d, то дан­ные прямые не пересекаются.

14. Три признака равенства треугольников.

15. Два перпендикуляра к одной и той же прямой не пересекаются.

16. Через точку, лежащую вне прямой, в плоскости, определяемой этой точкой и прямой, проходит по крайней мере одна прямая, не пере­секающая данной.

17. Сумма внутренних углов любого тре­угольника не более 2d (теорема Лежандра).

18. Все три биссектрисы любого треугольни­ка пересекаются в одной точке, расположенной внутри треугольника.

19. В любой треугольник можно вписать ок­ружность, и притом единственную.

20. Прямая пересекает окружность не более чем в двух точках.

21. Равные дуги окружности стягиваются равными хордами и наоборот.

22. В равнобедренном треугольнике биссек­триса угла при вершине является медианой и высотой.

Вместе с тем были вскрыты теоремы, завися­щие от V постулата и являющиеся его эквивалентами. Ниже приводим список основных эк­вивалентов V постулата на плоскости.

1. Через любую точку, взятую вне прямой, в плоскости, определяемой этой точкой и прямой, проходит одна и только одна прямая, параллель­ная данной (аксиома Плейфера, XVIII в.).

2. Геометрическое место точек, равноуда­ленных от данной прямой и расположенных по одну сторону от нее, на плоскости есть прямая линия (постулат Посидония, I в. до н. э.).

3. Расстояние между двумя параллельными прямыми есть величина постоянная (постулат Прокла, V в.).

4. Существуют хотя бы два подобных, но не равных треугольника (постулат Валлиса, XVII в.).

5. Через любые три точки, не лежащие на одной прямой, можно всегда провести окруж­ность (постулат Фаркаша Больяй, XIX в.).

6. Через любую точку, взятую внутри остро­го угла, можно провести всегда по крайней ме­ре одну прямую, пересекающую обе стороны этого угла (постулат Лежандра, XVIII в.).

7. Если прямая пересекает одну из двух не­пересекающихся прямых и лежит с ними в одной плоскости, то она пересекает и другую прямую.

8. Сторона вписанного в круг правильного шестиугольника равна радиусу этого круга.

9. Сумма внутренних углов прямолинейного треугольника равняется двум прямым.

10. Перпендикуляр и наклонная к одной и той же прямой, лежащие в одной плоскости, всегда пересекаются.

11. Существует треугольник с произвольно большой площадью.

12. Высоты треугольника всегда пересека­ются.

13. Теорема Пифагора: в прямоугольном тре­угольнике квадрат гипотенузы равен сумме квадратов катетов.

14. Внешний угол треугольника равен сумме внутренних углов, не смежных с ним.

15. Средняя линия треугольника равна половине его основания.

16. Через любую внутреннюю точку угла всегда можно провести прямую, пересекающую стороны угла.

Любое из этих предложений можно принять за аксиому, тогда V постулат и все зависящие от него предложения «Начал» Евклида будут доказаны, как теоремы.

В заключение беседы приведем три ложных доказательства V постулата Евклида, принадле­жащие Проклу, Валлису и Луи Бертрану.

Доказательство Прокла. В комментариях на I книгу «Начал» Евклида Прокл (410 - 485) при­водит свое доказательство V постулата, который он дает в форме: «Если прямая пересекает одну из параллельных прямых и лежит с ними в од­ной плоскости, то она пересекает и другую па­раллельную прямую».

Само доказательство он проводит так.

Пусть а и b - параллельные прямые и, пусть прямая с, находясь в одной плоскости с прямы­ми а и b, пересекает прямую b в точке М (рис. 2). Докажем, что при данных условиях прямая с пересечет прямую а.

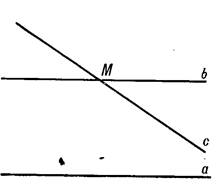
Рис. 2.

Такое пересечение действительно возможно, так как расстояние переменной точки луча Мс от прямой b возрастает неограниченно, если эта точка неограниченно удаляется от точки М, тог­да как расстояние между двумя параллельными прямыми есть всегда величина постоянная.

Рассуждение Прокла основано на использо­вании эквивалента V постулата. Этим эквива­лентом является утверждение, что расстояние между двумя любыми параллельными прямыми есть величина постоянная (постулат Прокла). Утверждение Прокла о расходимости пересека­ющихся прямых можно доказать. Теперь оно доказывается на основании предложений, не за­висящих от постулата параллельности. Таким об­разом, доказательство Прокла не лишено из­вестного «порочного круга» и терпит неудачу.

Доказательство Валлиса. 11 июля 1663 г. английский математик Джон Валлис (1616 - 1703), занимавший кафедру Евклида в Оксфорд­ском университете, прочитал лекцию по теории параллельных линий. Он полагал, что в этой лекции ему удалось строго доказать V постулат Евклида. В своих рассуждениях Валлис исходил из предложения о существовании подобных тре­угольников различной величины (постулат Валлиса).

Суть доказательства Валлиса коротко можно изложить следующим образом. Пусть прямые а и b (рис. 3) пересечены третьей АВ и образуют с ней внутренние односторонние углы α и β, сумма которых меньше двух прямых углов, т.е. α + β < 2d. Докажем, что в этом случае а и b обяза­тельно пересекутся в некоторой точке М. Чтобы в этом убедиться, будем перемещать прямую а не­прерывно от А к В так, чтобы она с прямой АВ сохраняла один и тот же угол α. В таком случае те точки прямой а, которые лежат внутри угла β, должны по пути обязательно пройти через пря­мую b, так как в положении b' все они лежат вне этого угла. Пусть N будет одна из точек пря­мой а (прямая а в новом положении на рисунке обозначена через с), попавшая на прямую b. Тогда получается треугольник CNB с углами α и β при основании СВ, где С - точка пересечения прямой с с пря­мой АВ, эти прямые образуют угол α. Теперь на отрезке АВ построим треугольник АМВ, подобный треугольнику CNB, что возможно согласно постулату Валлиса. По­скольку угол МАВ = α и угол MBA = β, прямая a пойдет по стороне AM, а прямая b - по стороне ВМ и, следовательно, прямые а и b пересекутся в точке М. Факт пересечения прямых а и b уста­новлен.

Рис. 3.

Казалось бы, постулат Валлиса позволил до­казать V постулат Евклида. Однако Евклид в своих «Началах» показал, что из V постулата вытекает следствие о существовании подобных, но не равных треугольников. Следовательно, приведенное доказательство Валлиса тоже не лишено порочного «логического круга».

Доказательство Бертрана. Швейцарский ма­тематик из Женевы Луи Бертран (1731 - 1812) в своем сочинении «Новое построение элементар­ной части математики», опубликованном в 1778 и 1812 гг., под влиянием распространявшихся идей математического анализа предпринял по­пытку нового доказательства V постулата Ев­клида. Вольно обращаясь с понятием «бесконеч­но малая величина», он в своих рассуждениях допустил ошибку, и поэтому его доказательство оказалось ложным.

Суть доказательства, предложенного Бертра­ном, заключается в следующем. Прежде всего несложными рассуждениями Бертран устанавли­вает, что так как две прямые а₁ и а₂, располо­женные в плоскости, пересечены третьей прямой b и образуют с ней внутренние односторонние углы α и β (рис. 4), сумма которых равна 2d, то часть плоскости, заключенная между прямыми а₁ и а₂, столь мала по отношению ко всей плос­кости, что содержится в ней бесконечное число раз. Действительно, как рассуждает Бертран, если полосу плоскости, заключенную между прямыми а₁ и а₂, передвигать вдоль прямой b так, чтобы точка А₂ совпала с точкой А₃, где А₂ и Аз - точки пересечения прямых а₂ и а₃ с прямой b, то она совпадет с полосой, заключен­ной между прямыми а₂ и а₃, так как совмещаются равные углы и соответственно совмещаются равные отрезки A₁A₂ и A₂A₃. Рассматривая на прямой b отрезки A₃A₄ = A₄A₅ = … = A_n-1A_n = A₁A₂,

на плоскости получим бесконечное множество равных полос, каждая из которых по отношений ко всей плоскости, по Бертрану, считается как угодно малой. Теперь легко доказывается и сам V постулат. Пусть прямые а и b пересечены третьей прямой с и пусть сумма внутренних од­носторонних углов α и β, образованных этими прямыми (рис. 5), меньше двух прямых углов, т.е. α + β < 2d. Докажем, что в этом случае пря­мые а и b пересекаются. Для доказательства через точку М (точка пересечения прямых а и с) проведем прямую а' так, чтобы прямая с с этой прямой а' и прямой b образовала внутренние од­носторонние углы, сумма которых равна 2d. Обозначим угол аМа через γ, которой во всей плоскости содержится раз, т.е. конечное чис­ло раз. Тогда а пересекает b. В противном слу­чае, если бы прямая а не пересекала прямой b, угол g, образованный прямыми а' и а, содержал­ся бы целиком внутри полосы, образованной пря­мыми а' и b, но это невозможно, так как g укладывается в плоскости конечное число раз, а вмещающая его полоса может быть уложена в плоскости сколько угодно раз.

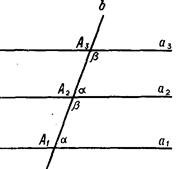
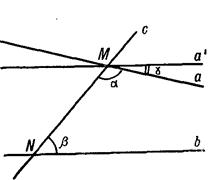
Рис. 4. Рис.5

Ошибка в рассуждениях Бертрана заключа­ется в том, что ни всю плоскость, ни часть ее, содержащуюся между сторонами угла, нельзя рассматривать как величину, допускающую точ­ное количественное определение, а поэтому их нельзя сравнивать и применять к ним обычные арифметические отношения.