Пути уменьшения неопределенностей

Неопределенность уменьшается при разработке и анализе альтернативных вариантов, дополнительном анализе неопределенных факторов (сбор и обработка недостающих исходных данных, выявление среди множества стратегий применения бесперспективных и определение расчетных), изменении параметров системы по мере ее разработки (в том числе принятие гибких технических решений).

Одним из путей снятия неопределенностей объектов, на которые направлены действия систем, действий реального противника или партнера является выбор наихудших параметров объектов, стратегий и условий применения, что дает возможность использовать проектируемую систему во всем рассматриваемом диапазоне стратегий и условий применения. Этот подход неизбежно приводит к исследованию частоты наступления наихудших параметров объектов обслуживания, стратегий и условий применения и последующего принятия решения о необходимости их реализации рассматриваемой системой.

Неопределенность может быть учтена при равнозначимом анализе, который предполагает:

- определение частных производных критерия эффективности по неопределенным параметрам,

- выделение групп параметров равного влияния, ранжированием групп в порядке убывания их влияния - выделение значимой части той или иной неопределенности, исследование влияния "малых" неопределенностей на критерий эффективности. Например, ограничение числа стратегий применения системы проводится на основе сопоставления степени влияния каждой стратегии и неопределенных параметров на эффективность. Если влияние стратегии применения сопоставимо с влиянием неопределенности самих параметров, то такие стратегии могут не рассматриваться.

Один из путей снятия неопределенности - предусмотреть возможность изменения (адаптации) параметров системы в зависимости от будущих конкретных ситуаций - выбор гибких технических решений, которые могут обеспечивать наиболее рациональное сочетание параметров при уточнении неопределенных факторов. Обоснованный выбор таких решений возможен на основе исследования эффективности систем в условиях неопределенности их применения.

4 ВИДЫ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ

4.1 Классификация математических моделей

Появление большого количества моделей самого различного типа привело к необходимости упорядочивания, классификации моделей, что является одним из условий грамотного применения моделей. Классификация необходима для ответа на вопросы: Какого вида модель более всего подходит для решения поставленной задачи? К какому классу относится разрабатываемая модель и в чем особенности ее использования?

Единая классификация видов модели затруднительна в силу многозначности понятия "модель" в науке и технике.

Математическая модель - это математическое представление реальности: система математических соотношений, описывающих процесс или явление.

Первой системой математических моделей, адекватно отражающих обширный класс процессов и явлений реального мира в конкретной области, стала классическая механика. Одной из основных задач классической механики была задача прогнозирования движения различных тел и сред. Любая модель механического движения представляет собой систему дифференциальных уравнений относительно координат и скоростей движущегося объекта – из необходимости моделирования и прогнозирования движения возникло дифференциальное исчисление.

Информационная модель - совокупность информации, характеризующая существенные свойства и состояния объекта, процесса, явления, а также взаимосвязь с внешним миром.

В качестве информационной модели могут служить наглядные изображения (фото, кино, видео), знаки (текст, знаковое табло), графические модели (график, чертеж, блок–схема) и комбинированные изображения (мнемосхема, карта). Это модели, созданные на естественном языке и формальном языке (т.е. научном, профессиональном или специализированном). Примеры формальных моделей: все виды формул, таблицы, графы, карты, схемы и т.д.

В основу классификации математических моделей могут быть положены различные принципы отображения объекта - классификационные признаки, отражающие те или иные особенности моделируемой системы (или их сочетания), например:

- по характеру моделей (т.е. по средствам моделирования);

- по характеру моделируемых объектов;

- по сферам приложения модели (модели в технике, в физических науках, в химии, экономике, модели процессов живого, модели психики и т. п.) и его уровням ("глубине"), начиная, например, с выделения в физике модели на микроуровне (модели на уровнях исследования, касающихся элементарных частиц, атомов, молекул).

Возможные классификационные признаки моделей: в зависимости от целей моделирования, в зависимости от способа получения моделей, в зависимости от оператора модели, в зависимости от параметров модели, в зависимости от методов реализации.

Большое количество возможных классификационных признаков породило много классификаций моделей, которые характеризуют их свойства, особенности применения, происхождения. Классификация моделей – это тоже элементарное моделирование.

В связи с этим любая классификация методов моделирования обречена на неполноту, тем более, что терминология в этой области опирается не столько на "строгие" правила, сколько на языковые, научные и практические традиции в конкретной области, а еще чаще определяется в рамках конкретного контекста и вне его никакого стандартного значения не имеет (типичный пример - термин "кибернетическое" моделирование).

При таком подходе выбор класса модели (классификация) является неотъемлемой частью построения модели - выбор класса модели можно рассматривать как выбор структуры модели - с позиций структурного моделирования.

Исследуемая система и ее модель могут относиться как к одному, так и к разным классам. Например, реальная система может быть подвержена воздействию случайных факторов и, соответственно, будет относиться к классу стохастических систем. Если разработчик модели считает, что влиянием этих факторов можно пренебречь, то создаваемая модель будет представлять собой детерминированную систему. Аналогичным образом возможно отображение системы с непрерывным временем смены состояний в модель с дискретными переходами и т. д.

Схема классификации систем важна не сама по себе. На этапе разработки концептуальной модели она, во-первых, позволяет уточнить цели и задачи моделирования и, во-вторых, облегчает переход к этапу формализации модели. Кроме того, на этапе оценки качества разработанной модели, знание классификационных признаков дает возможность оценить степень ее соответствия первоначальному замыслу разработчика.

Любая система может представляться некоторым набором, отличающихся друг от друга, моделей. Отличия могут содержаться в степени детализации и учете различных особенностей режимов функционирования. Могут отражаться некоторые грани сущности системы, можно ориентироваться на анализ некоторых наборов свойств. Поэтому разработке модели и ее классификации, естественно, предшествует постановка (формулировка) цели моделирования.

В зависимости от целей моделирования могут быть выделены моделипо классификационному признаку:

- «установление законов изменения параметров модели» - описательные модели;

- «изучение преобразования объектом входных сигналов» - функциональные модели;

- «изучение внутренней структуры объекта» - структурные модели;

- «определение оптимальных параметров объекта или режима управления объектом» - оптимизационные модели;

- «принятие эффективных управленческих решений»- управленческие модели.

Описательные модели являются реализацией содержательных и концептуальных моделей – позволяют определять параметры модели в зависимости от принятых условий и гипотез.

Функциональные модели отражают происходящие физические, механические, химические, информационные и др. процессы. Комбинированные структурно-функциональные модели отражают устройство и функционирование объекта.

Структурные модели – отражают устройство объекта и связи (в том числе типы связей) между его элементами.

В структурной модели можно выделить два типа - топологическую и геометрическую модели.

Топологическая модель отражает состав объекта и связи между его элементами. Такая модель обычно строится на основании структурной схемы и имеет форму графов, таблиц, матриц, списков.

Возможные типы связей: в материаловедении – типы кристаллических решеток и их симметричность, в информационных системах – направление и интенсивность передачи информации, организационных системах – иерархия в процессе принятия решений и распределение ответственности за решения.

Геометрическая модель в дополнение к топологической содержит сведения о форме и размерах объекта и его элементах, об их взаимном расположении.

В геометрическую математическую модель обычно входят совокупность уравнений линий и поверхностей, а также соотношения, определяющие принадлежность областей пространства телу или элементу.

Оптимизационные модели содержат свободные параметры или функции (оптимизируемые параметры, параметры режимов управления), управление ними (их изменение) выбирается из условия достижения системой заданной цели - заданного критерия (критериев) эффективности выполнения системой своих задач.

В оптимизационных можно выделить управленческие модели. Из управленческих моделей можно выделить кибернетические модели – имеется несколько субъектов управления, обладающих собственными целями (модели используются для разрешения конфликтных ситуаций).

Примеры возможных классификаций.

Признаки классификации	Виды математических моделей
Принадлежность к иерархическому уровню	Модели микроуровня Модели макроуровня · Модели метауровня
Тип моделирования	Эмпирическая Теоретическая · Смешанная
Характер взаимоотношений со средой	Открытые (непрерывный обмен) · Закрытые (слабая связь)
Характер отображаемых свойств объекта	· Структурные · Функциональные
Способ представления свойств объекта	· Аналитические · Алгоритмические · Имитационные
Способ получения модели	· Теоретические · Эмпирические
Причинная обусловленность	· Детерминированные · Вероятностные
Отношение к размерности пространства	· Одномерные · Двумерные · Трехмерные
Отношение к времени	· Динамические · Статические
Тип уравнений	· Линейные · Нелинейные
множество значений переменных	· Непрерывные · Дискретные · Дискретно-непрерывные
Назначение	· Технические · Экономические · Социальные и т.д.

В зависимости от способа получения выделяются теоретические и эмпирические модели.

Теоретические модели получают в результате изучения свойств систем, явлений, процессов, эмпирические модели являются итогом обработки результатов наблюдений внешних проявлений этих свойств и процессов.

Среди теоретических моделей можно выделить три группы моделей – феноменологические, асимптотические и модели ансамблей.

Феноменологические модели - построенные по результатам прямого наблюдения объекта, явления, его осмысливания.

Асимптотические модели - построенные в результате процесса дедукции, как частный случай более общей модели.

Модели ансамблей - построенные в результате обобщения (синтеза) отдельных моделей (процесс индукции).

Такие модели не могут быть получены путем механического объединения моделей отдельных объектов в модель системы, поскольку внутренние свойства системы при объединении объектов могут изменяться (например, в социально-экономических системах). Свойство каждого объекта исследуются с учётом взаимодействия его с другими объектами системы.

В зависимости от параметров могут быть выделены модели по классификационному признаку:

- «состав параметров» - дискретные, непрерывные, качественные, количественные, смешанные модели;

- «вид используемой информации» - детерминированные (каждому параметру соответствует конкретное число или функция) или неопределенные (стохастические - значения всех или некоторых параметров определяются случайными величинами, нечеткие - значения всех или некоторых параметров описываются функциями принадлежности соответствующему нечеткому множеству, случайные, нечеткие) модели;

- по отношению ко времени – статические и динамические (стационарные и нестационарные):

- по отношению к размерности пространства – одномерные, двухмерные, трехмерные.

В зависимости от методов реализации - аналитические (алгебраические и приближенные) и алгоритмические (численные и имитационные) модели.

Аналитическое моделирование основывается на косвенном описании реального объекта с помощью набора математических выражений, которые образуют аналитическую модель. За счет огрубления действительности они позволяют сосредоточить внимание на существе явления, его основных закономерностях, а уточнение и конкретизация решений выполняется на статистических моделях.

Для аналитического моделирования характерно то, что процессы функционирования исследуемой системы записываются в виде некоторых функциональных соотношений (алгебраических, интегро-дифференциальных, конечно-разностных и т.п.) или логических условий. В них устанавливаются формульные, аналитические зависимости между параметрами системы. Для описания этих зависимостей разработан язык алгебраических, дифференциальных, интегральных и др. уравнений.

Наиболее полное исследование процесса функционирования системы можно провести, если известны явные зависимости, связывающие искомые характеристики с начальными условиями, параметрами и переменными системы. Однако такие зависимости удается получить только для сравнительно простых систем. При усложнении систем исследование их аналитическим методом наталкивается на значительные трудности.

Для задач, требующих учета большого количества факторов, в том числе и случайных или нечётких (неопределённых), разработаны методы имитационного моделирования. Имитационное моделирование основано на прямом описании моделируемого объекта, используя структурное подобие объекта и модели, т.е. каждому существенному, с точки зрения решаемой задачи, элементу объекта ставится в соответствие элемент модели.

Схема классификации систем важна не сама по себе. На этапе разработки концептуальной модели она, во-первых, позволяет уточнить цели и задачи моделирования и, во-вторых, облегчает переход к этапу формализации модели. Кроме того, на этапе оценки качества разработанной модели, знание классификационных признаков дает возможность оценить степень ее соответствия первоначальному замыслу разработчика.

Исследуемая система и ее модель могут относиться как к одному классу, так и к разным классам. Например, реальная система может быть подвержена воздействию случайных факторов и, соответственно, будет относиться к классу стохастических систем. Если разработчик модели считает, что влиянием этих факторов можно пренебречь, то создаваемая модель будет представлять собой детерминированную систему. Аналогичным образом возможно отображение системы с непрерывным временем смены состояний в модель с дискретными переходами и т. д.

Рассмотрим классификацию технических систем, параметры которых определяют соответствующий класс моделей.

Исследуемый объект (процесс) может быть распределенным или сосредоточенным в пространстве и одновременно изменяться во времени. Соответственно могут быть модели с распределенными и сосредоточенными в пространстве параметрами.

Если основные переменные процесса не изменяются в пространстве, а только во времени и не зависят от прочих координат, то математическая модель, описывающая такие процессы - модель с сосредоточенными параметрами. Такие модели представляются в виде обыкновенных дифференциальных уравнений.

Для систем с распределенными параметрами переменные зависят как от времени, так и от прочих координат. В зависимости от задачи одна и та же система может рассматриваться и как система с сосредоточенными параметрами и как система с распределенными параметрами. Например, нельзя указать точные границы для тока в проводе. Что касается классов моделей, то здесь имеется четкая граница. Системы с распределенными параметрами описываются с помощью дифференциальных уравнений в частных производных.

Если процесс развивается одновременно и во времени, и в пространстве (по одной координате l), то оператор А может преобразовывать входную векторную функцию X(t, l) в выходную векторную функцию Y(t, l) и зависеть от обоих аргументов: A=A(t,l).

Пример. Рассмотрим твердый брус, нагреваемый с одной стороны и изолированный с другой. Соотношение между температурой, временем и расстоянием от точки нагрева описывается дифференциальным уравнением в частных производных Температура в этом уравнении является функцией двух переменных: времени t и расстояния l, т.е. в любой момент времени t_i температура изменяется с изменением расстояния l_i. или, наоборот, в любом месте l_i температура изменяется со временем.

Жесткие и мягкие модели

Пример представления модели различной сложности и классификации.

Механическая система состоит из пружины, закрепленной с одного конца, и груза массой m, прикрепленного к свободному концу пружины. Груз может двигаться только в направлении оси пружины (например, движение происходит вдоль стержня). При смещении из положения равновесия груз испытывает действие возвращающей силы – система совершает колебания.

Математическая модель этой системы описывает состояние системы: расстояние x от центра груза до его положения равновесия.

Взаимодействие пружины и груза описывается с помощью закона Гука (F = − kx) и второго закона Ньютона (в форме дифференциального уравнения):

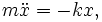
где 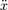означает вторую производную от x по времени: .

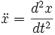По формальной классификации эта модель линейная, детерминированная, динамическая, сосредоточенная, непрерывная. В процессе ее построения было сделано множество допущений (об отсутствии внешних сил, отсутствии трения, малости отклонений и т.д.), которые в реальности могут не выполняться.

По отношению к реальности это упрощенная модель, поскольку опущены некоторые существенные универсальные особенности (например, рассеяние энергии за счет трения, изменения жесткости пружины при значительном отклонении). В некотором приближении (пока отклонение груза от равновесия невелико, при малом трении, в течение не слишком большого времени и при соблюдении некоторых других условий), такая модель достаточно хорошо описывает реальную механическую систему, поскольку отброшенные факторы оказывают пренебрежимо малое влияние на ее поведение. Однако модель можно уточнить, приняв во внимание какие-то из этих факторов. Это приведет к новой модели, с более широкой (хотя и снова ограниченной) областью применимости.

При уточнении модели сложность ее математического исследования может существенно возрасти и сделать модель фактически бесполезной. Зачастую более простая модель позволяет лучше и глубже исследовать реальную систему, чем более сложная (и, формально, «более правильная»).

Модель гармонического осциллятора можно применять к объектам, далеким от механики - ее содержательный статус может быть другим (например, при приложении этой модели к биологическим популяциям).

Гармонический осциллятор — пример так называемой «жесткой» модели. Она получена в результате сильной идеализации реальной физической системы. Для решения вопроса о ее применимости необходимо понять, насколько существенными являются факторы, которыми мы пренебрегли. Иными словами, нужно исследовать «мягкую» модель, получающуюся малым возмущением «жесткой». Она может задаваться, например, следующим уравнением:

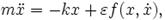
Здесь — некоторая функция, в которой может учитываться сила трения или зависимость коэффициента жёсткости пружины от степени её растяжения, — некоторый малый параметр. Явный вид функции f нас в данный момент не интересует. Если мы докажем, что поведение мягкой модели принципиально не отличается от поведения жёсткой (вне зависимости от явного вида возмущающих факторов, если они достаточно малы), задача сведется к исследованию жёсткой модели. В противном случае применение результатов, полученных при изучении жёсткой модели, потребует дополнительных исследований. Например, результатом решения уравнения гармонического осциллятора могут быть колебания с постоянной амплитудой. Следует ли из этого, что реальный осциллятор будет бесконечно долго колебаться с постоянной амплитудой? Нет, поскольку рассматривая систему со сколь угодно малым трением (всегда присутствующим в реальной системе), мы получим затухающие колебания. Поведение системы качественно изменилось.

Если система сохраняет свое качественное поведение при малом возмущении, говорят, что она структурно устойчива. Гармонический осциллятор — пример структурно-неустойчивой (негрубой) системы. Тем не менее, эту модель можно применять для изучения процессов на ограниченных промежутках времени.

4.2 Классификация математических моделей в зависимости от оператора модели

Любая математическая модель может рассматриваться как некоторый оператор – алгоритм или совокупность уравнений. Наиболее распространенный в математическом моделировании вид оператора – функция. Конкретное задание функции связано с построением математической модели системы – на выбор функции накладываются ограничения, вытекающие из содержательной постановки задачи.

Классификационные признаки при классификации в зависимости от оператора:

- «вид зависимости выходных параметров от значений входных параметров» - линейные или нелинейные модели;

- «вид функциональной зависимости» - алгебраические, дифференциальные (обыкновенные, в частных производных), интегродифференциальные и др. уравнения или системы уравнений.

Линейные и нелинейные модели

Линейность или нелинейность анализируемого процесса оказывает решающее влияние на вид модели, метод программирования.

В основу разработки линейной модели положена гипотеза линейного представления реального нелинейного мира.

Линейная модель - оператор обеспечивает линейную зависимость выходных параметров от входных - линейное соотношение (прямая пропорциональная зависимость) между двумя числовыми переменными.

Модель описывается линейной функцией вида у = кх + в.

Линейная функция нескольких переменных y = a₀ + a₁x₁ +…a_nx_n.

Если задача многомерна – система уравнений.

В линейной модели объекта его параметры связаны линейно - при изменении какого-либо параметра линейное соотношение модели предсказывает линейное изменение зависящего от него выходного параметра, при изменении двух и более параметров - сложение их влияний, линейная модель обладает свойством суперпозиции. Общая реакция системы на входные реакции равна сумме реакций на каждую входную.

Множества входов X, состояний Z и выходов Y – линейные пространства, операторы переходов входов в состояния α и состояний в выходы β – линейные операторы (одновременно однородны и аддитивны).

Использование такой зависимости позволяет описывать многие процессы в реальных системах (это и закон Ньютона и закон Гука в механике, и закон Ома в электротехнике).

Геометрический образ линейной функции, каков бы ни был ее физический смысл, в зависимости от числа независимых переменных — прямая, плоскость. На одинаковые приращения независимой переменной линейная функция (то есть независимо от значения независимой переменной) откликается одинаковыми приращениями. Это означает, что линейная зависимость не обладает избирательностью. Она не может описывать ни резонансных всплесков, ни насыщения, ни колебаний — ничего, кроме равномерного неуклонного роста или столь же равномерного и столь же неуклонного убывания.

В более общем случае, если не учитывается воздействие случайных факторов, а малые изменения входных воздействий приводят к такого же порядка малым изменениям выходного воздействия и состояниям системы, модель можно представить в виде векторного дифференциального уравнения

dy/dt = F(x(t), v(t),g(t) t),

где F – вектор-функция закона функционирования системы; – x, v, h, y - векторы входных, внутренних, управляющих и выходных воздействий соответственно.

В случае линейности систем, когда переменные обладают свойством однородности и аддитивности, вид уравнений упрощается, что позволяет решать их аналитическими или численными (приближенными) методами. Благодаря простоте линейные модели широко применяются, хотя большинство процессов – нелинейно.

Линейность – свойство системы, которое позволяет делать выводы о поведении системы для всего класса входных воздействий, основываясь на том, как она реагирует лишь на некоторые из них. Общая реакция системы на входные воздействия является суммой отдельных реакций.

Основное свойство линейных систем – выполнение принципа суперпозиции решений: линейной комбинации произвольных входных сигналов ставится в соответствие та же линейная комбинация сигналов на выходе из системы: любая линейная комбинация решений также является решением задачи, т.е. если известны решения Y₁при Х₁ и Y ₂ при Х₂, то решение для выходных параметров при Х =Х₁ + Х₂ есть Y= Y₁ +Y₂.

Пусть на одном интервале t₀t заданы два фрагмента Х_t0t' и Х_t0t'' различных входных процессов Х_Т' и Х_Т'', а в момент времени t₀ - два различных состояния z' (t₀) и z'' (t₀). Введем в рассмотрение фрагменты Х_t0t = Х_t0t' + Х_t0t'' и кХ_t0t , а также состояния z (t₀) = z' (t₀) + z'' (t₀) и к z (t₀).

По отношению к операциям умножения и сложения операторы могут быть однородны и аддитивны.

Операторы α и β однородны, если

α (t₀t, к z (t₀), кХ_t0t) = к α (t₀t, z (t₀), Х_t0t);

β (t₀t, к z (t₀), кХ_t0t) = к β (t₀t, z (t₀), Х_t0t).

Операторы α и β аддитивны, если

α (t₀t, z (t₀), Х_t0t) = α (t₀t, z' (t₀), Х'_t0t) + α (t₀t, z'' (t₀), Х''_t0t);

β (t₀t, z (t₀), Х_t0t) = β (t₀t, z' (t₀), Х'_t0t) + β (t₀t, z'' (t₀), Х''_t0t).

Принцип суперпозиции предполагает

[x (t) = x₁ (t) + x₂ (t)] → [y (t) = y₁ (t) + y₂ (t)],

где x₁ (t) и x₂ (t) - некоторые входные воздействия, а y₁ (t) и y₂ (t) - выходные отклики на каждый из них в отдельности.

Конечное состояние системы определяется как сумма состояний, в которые перешла бы система под воздействием фрагментов входных воздействий.

Линейные системы дают возможность разложения величин z (t) и y (t) на составляющие, изучение которых можно проводить независимо друг от друга.

О качественных свойствах общего случая можно судить по свойствам частного – различие между решениями носит только количественный характер. Или: в случае линейных моделей отклик системы на изменение каких-либо условий пропорционален величине этого изменения.

Линейной моделью представляются простые объекты, она полезна в начале цепочки моделей, последовательно приближающихся к модели с требуемой адекватностью. Линейная модель часто позволяет сразу получить оценку порядка значений выходных переменных.

Нелинейная модель не подчиняется принципу суперпозиции, знание о поведении части системы еще не гарантирует знания поведения всей системы, а ее отклик на изменение каких-либо условий может качественно зависеть от величины этого изменения.

Иногда нелинейную задачу удается свести к последовательности линейных. Линеаризацией нелинейной задачи можно получить линейную модель для достаточно корректной оценки воздействия на систему малых возмущений.

То, что точно схватывает и передает характерные особенности одного класса нелинейных функций, ничего не говорит даже о простейших особенностях типичного представителя другого класса. Геометрический образ нелинейной функции — кривая на плоскости, искривленная поверхность. На одинаковые приращения независимой переменной одна и та же нелинейная функция откликается по-разному в зависимости от того, какому значению независимой переменной придается приращение.

Почти полным безразличием к изменению одних и повышенной чувствительностью к изменению других значений независимой переменной нелинейные функции резко отличается от линейных. Именно здесь и проходит демаркационная линия между миром нелинейных и миром линейных явлений.

В какой бы области естествознания ни возникала нелинейность явлений, она глубоко «функциональна». В физике нелинейность — это учет различного рода взаимодействий, обратных влияний и тонких эффектов, не учитываемых в линейной постановке. В химии нелинейность отражает обратные связи в скрытых механизмах реакций. В биологии нелинейность имеет эволюционный смысл: только сильная нелинейность позволяет биологическим системам охватить громадный диапазон жизненно значимых малых воздействий среды. Те, которые не сумели этого сделать - вымерли, не выдержав борьбы за существование. На их могилах можно было бы написать: «Они были слишком линейными для этого мира»

Вопрос о возможности и целесообразности перехода от нелинейности к линейности решается в каждой задаче конкретно на рациональном уровне.

Большинство реальных процессов нелинейны, а линейные их модели отвечают весьма частным случаям и, как правило, служат первым приближением к реальности.

Нелинейные уравнения можно разделить на два подкласса: алгебраические, в которых над переменными производятся только действия сложения, вычитания, умножения, деления и возведения в степень с рациональным показателем, и трансцендентные, в которые входят другие функции от переменных (показательные, тригонометрические и др.). В любом случае сложность модели существенно зависит от числа уравнений и вида входящих в них функций. Обычно наиболее просто решаются алгебраические уравнения 1-й степени (линейные), наиболее сложно – трансцендентные.

Пример – закон Гука о линейной зависимости перемещения от растягивающей силы F = - кx. Упругость означает существование однозначной монотонно возрастающей функции, связывающей напряжение s = F/S (S - площадь поперечного сечения) и деформацию ε = x/l (x – относительное перемещение концов, l – длина образца): s = f (ε), f (0) = 0. Функция f в общем случае нелинейная. Нелинейными упругими свойствами обладают, например, высокоэластичные резиновые шнуры – ели такой шнур растянуть в десять раз (ε = 0,9), а затем отпустить, он восстановит свою длину. Если длинные металические проволоки подвергать малым деформациям (ε = 0,001), нелинейность не обнаруживается. При растяжении металлического стержня по мере возрастания растягивающего напряжения s деформация ε сначала растет по линейному закону. Это означает, что при таких ε первый член разложения функции s = f (ε) (полагая ее аналитической) в степенной ряд s = ε ∂f /∂ε + ½! ε²∂²f /∂ε² + ... значительно превосходит все остальные. Тогда s = Еε (Е – модуль упругости материала при его одноосном сжатии). Нелинейный закон – параболическая зависимость

s = Аε - Вε².

Применение иерархического подхода позволяет на определенном этапе моделирования принимать упрощающие предположения, например, о линейности моделей.

Линейные модели занимают определенную нишу в исследованиях – любая линейная теория ограничена в определенных пространственных и временных рамках при малых интенсивностях воздействий на систему. Например, в строительстве не учитывают кривизну Земли, в космической технике не прибегают к теории относительности при несоизмеримых скоростях.

Методы исследования линейных систем очень развиты и обоснованное применение линейной модели для нелинейной системы часто оказывается весьма эффективным.

Если нелинейность является принципиальной, то применение линейных систем не дадут даже качественной картины процесса.

Например, закон тяготения изначально нелинейный (квадратичная зависимость силы взаимодействия между массами), и потому основанные на нем модели также нелинейны. Нелинейность может быть также обусловлена геометрией явления, изменением состояния (изменение жесткости пружины при исследовании колебательного процесса).

Источником нелинейности могут быть различные причины. Обычно принято считать, что при малых (не всегда) отклонениях системы от положения равновесия соотношения между перемещениями или скоростями ее элементов и возникающими силами линейны.

Например, силы трения между поверхностями (поверхности разделены смазочным материалом жидкостью или газом) линейно зависят от скорости перемещения поверхностей, с увеличением скорости эта зависимость становится нелинейной – вязкое трение зависит от квадрата скорости (турбулентное трение).

Обыкновенные дифференциальные модели

Одна из основных задач классической механики - задача прогнозирования движения различных тел и сред – решается на основе математической модели механического движения, которая представляет собой систему дифференциальных уравнений относительно координат и скоростей движущегося объекта. С помощью дифференциальных моделей решается большинство задач механики, гидродинамики, электродинамики и др.

Дифференциальное уравнение – уравнение, содержащее неизвестную функцию одного или нескольких переменных, независимые переменные и производные неизвестной функции по независимым переменным.

Обыкновенное дифференциальное уравнение – уравнение, в котором неизвестной является функция от одного независимого переменного, причем, в это уравнение входят не только сама неизвестная функция, но и ее производные различных порядков:

F[x, y(x), y’(x), …, y⁽ⁿ⁾(x)] = 0.

Общее решение: y = y(x, C₁,…, C_n), при любом наборе С – частное решение.

Задача Коши (задача с начальными условиями) – задача о нахождении частного решения, которое удовлетворяет n частным условиям y(x₀) = y₀, y’(x₀) = y’₀,…, y^(n-1)(x₀) = y^(n-1) ₀.

Система обыкновенных дифференциальных уравнений для r неизвестных функций имеет вид

F_i[x, y₁, y₂, …,y_r, y’₁, y’₂,…, y’_r,…, yⁿ₁, yⁿ₂, …, yⁿ_r] = 0 , i = 1,…, r.

Линейное обыкновенное дифференциальное уравнение – линейно относительно искомой функции, независимого переменного и ее производной, т.е. уравнение вида

y⁽ⁿ⁾ + a₁(x)y^(n-1) + … + a_n-1(x)y¹ + a_n(x)y = f(x),

y(x) – искомая функция, a_i(x), f(x) – заданные функции.

Задача прогнозирования движения (задача математического анализа) решается интегрированием дифференциальных уравнений движения при заданных начальных условиях (задача Коши) - пассивный расчет траектории движения объекта. Усложнение задачи – определить, какими должны быть начальные скорости объекта, чтобы из одного заданного положения он переместился в другое заданное – здесь уже присутствует элемент управления движением. Дальнейшее усложнение – траектория движения из одного положения в другое должна обладать определенным экстремальным свойством, например, минимальное время движения (задача о брахистохроне).

Законы механики – описание движения системы точек или твердого тела могут быть сведены к задаче нахождения решений ОДУ. Анализ устойчивости движения, химические реакции, теория колебаний, теория оптимального управления представляют собой динамические системы и могут быть формализованы ОДУ.

Процесс составления дифференциального уравнения по условию задачи (физической, технической) состоит в выражении на математическом языке связи между переменными величинами и их бесконечно малыми приращениями. Модели, описываемые обыкновенными дифференциальными уравнениями, в которых неизвестные функции зависят только от одной переменной - обыкновенные дифференциальные модели.

Построение обыкновенных дифференциальных моделей зависит от законов в конкретной предметной области.

Ответы на вопросы, поставленные при построении дифференциальной модели, получают после интегрирования дифференциальных уравнений. Большинство дифференциальных уравнений не может быть проинтегрировано в замкнутой форме (даже если известно, что такое решение имеется), т.е. не удается представить решение в виде аналитической зависимости, использующей конечное число операций над элементарными функциями (решение в виде бесконечного ряда далеко не всегда позволяет исследовать необходимые свойства).

Приемы и методы, которые позволили бы, не решая самих дифференциальных уравнений, получать необходимые сведения о тех или иных свойствах решений, предоставляет качественная теория дифференциальных уравнений.

В основе этой теории лежат общие теоремы о существовании и единственности решений, о непрерывной зависимости решений от начальных параметров. Численному интегрированию дифференциальных уравнений обязательно должно предшествовать обращение к теоремам существования и единственности.

4.3 Классификация математических моделей в зависимости от параметров модели

Непрерывные и дискретные модели

Процесс функционирования системы может протекать непрерывно или дискретно. Решение о дискретности или непрерывности модели принимается на этапе постановки задачи также на рациональном уровне.

Непрерывной во времени модель является в том случае, когда характеризующая ее переменная определена для любого значения времени; дискретной во времени - если переменная получена только в определенные моменты времени.

Дискретность модели непрерывных систем может также возникнуть в том случае, если она состоит из непрерывных компонентов, но информация переходит от одной компоненты к другой по заданной схеме (такие переходы возможны только по окончании соответствующих операций).

Непрерывная система функционирует в непрерывном времени (интервал ее функционирования T = [t₀, t_k] представляет собой отрезок оси действительных чисел, заданный началом t₀ и концом t_k), непрерывно изменяется состояние системы (непрерывны операторы α и β). Малые изменения входных воздействий приводят к такого же порядка малым изменениям состояния системы и выходных воздействий.

Модель непрерывная, если она описывает поведение системы для всех моментов времени из некоторого промежутка.

Модель S = gt²/2, 0 < t < 100 непрерывна на промежутке времени (0; 100).

Непрерывные модели применяются при изучении систем, связанных с непрерывными процессами, которые описываются с помощью систем дифференциальных уравнений, задающих скорость изменения переменных системы во времени. Непрерывные модели можно описать с помощью конечно-разностных уравнений, которые в пределе переходят в соответствующие дифференциальные уравнения.

Дискретная система функционирует в дискретном временном пространстве и определяется дискретными состояниями - изменения ее состояния происходят лишь в дискретные моменты времени (дискретный интервал функционирования).

Дискретными могут быть системы, для которых дискретным является или только время, или только состояния. Это широкий и практически важный класс систем – в него входят все дискретные (цифровые, измерительные, управляющие и вычислительные, в том числе ЭВМ) устройства.

Дискретность временного пространства означает, что явления, сопровождающие изменения состояния системы, могут происходить лишь в моменты времени, образующие некоторое дискретное множество, в котором моменты времени можно пронумеровать. В частности, переходы системы из одного состояния в другое могут осуществляться в целочисленные моменты времени. Общий случай сводится к этому частному введением целочисленной нумерации моментов возможных изменений состояний.

Если рассматривать только t - 0, 1, 2, ..., 10 (с), то модель S₁ = gt²/2, или числовая последовательность S₀ = 0, S = g/2, S₂ = 2g, S₃ = 9g/2, ..., S₁₀= 50g, может служить дискретной моделью движения свободно падающего тела.

Непрерывная система может рассматриваться как дискретная. Это достигается путем учета ее состояния лишь в отдельные моменты времени и округления их значений до целых единиц.

Системы с дискретными состояниями характеризуются тем, что в любой момент времени можно однозначно определить, в каком именно состоянии находится система. Для такой идентификации обязательно нужно знать тот признак, который отличает одно состояние системы от другого. Например, при исследовании систем массового обслуживания в качестве такого признака обычно используют число заявок в системе. Соответственно, изменение числа заявок в системе интерпретируется как переход системы в новое состояние.

Если же не удается подобрать такой признак, либо его текущее значение невозможно зафиксировать, то систему относят к классу систем с непрерывным множеством состояний.

Смена состояний может происходить либо в фиксированные моменты времени, множество которых дискретно (например, поступление новых заявок на обслуживание), либо непрерывно (изменение температуры тела при нагревании). В соответствии с этим различают системы с дискретным временем переходов (смены состояний) и системы с непрерывным временем переходов(точнее, «живущие» в непрерывном времени).

Дискретными могут быть системы с дискретным вмешательством случая – эти системы почти всегда ведут себя как непрерывные и только в дискретные моменты времени испытывают случайные воздействия. По условиям перехода из одного состояния в другое системы могут быть детерминированными или стохастическими.

Дискретизация (преобразование непрерывной функции в дискретную) применяется в системах передачи, хранения и обработки информации, поступающей в виде непрерывных сигналов.

Например, передача фото или телевизионных изображений (функция двух или трех переменных) осуществляется путем разбивки на дискретные строки. Передача звука (функция одной переменой) с помощью импульсно-кодовой модуляции сопряжена с дискретизацией непрерывного сигнала и последующим кодированием (модуляция – изменение параметров некоторого физического процесса во времени в соответствии с текущим значением сигнала).

В модели функционирования дискретной системы предполагается дискретность интервала функционирования T = [t₀, t_k].

Дискретизация по времени обычно выполняется так, чтобы интервал t = t_n+1 - t_n между ближайшими в множестве Т моментами времени t_n+1 и t_n был один и тот же для всех n. Тогда t называется временем такта, а моменты t_n - тактами функционирования системы.

Фрагменты входного и выходного процессов дискретной системы представляются в виде пронумерованных последовательностей входных и выходных воздействий:

Х_t0t = {x(l), x(l + 1), . . ., x(g)} = Х_lg;

У_t0t = {у(l), у(l + 1), . . ., у(g)} = У_lg,

однозначно задаваемых номерами первого l и последнего g тактов функционирования системы. Тогда модель функционирования дискретной системы:

z (g) = α (lg, z (l), Х_lg);

у (g) = β (lg, z (l), Х_lg).

Если фрагмент входного процесса Хlg разбить на два подфрагмента и представить его как их объединение, то уравнения состояния и выхода в дискретной системе имеют вид:

z (n+1) = α (n, z (n), x (n), x (n+1));

у (n+1) = β (n, z (n), x (n), x (n+1)),

где α и β - функции действительных переменных n, z (n), x (n) и x (n+1).

Величина x (n+1) не влияет на z (n+1), если состояние системы изменяется с некоторой задержкой относительно момента поступления входного воздействия. При этом

z (n+1) = α (n, z (n), x (n)).

Выходное воздействие у (n+1) определяется значениями z и x в том же (n+1)–м такте, и потому

у (n) = β (n, z (n), x (n)).

Изучением свойств непрерывного характера занимается классическая математика. В дискретной математике отказываются от основополагающих понятий классической математики – предела и непрерывности.

Использование классической или дискретной математики зависит от задач исследований – какая модель явления рассматривается – дискретная или непрерывная. Основные разделы дискретной математики: математическая логика, вычислительная математика (численное интегрирование), теория графов (задачи анализа структур, экономические задачи, электротехнические задачи – трассировка), теория кодирования (хранение, обработка, передача информации), теория функциональных систем (описание функционирования сложных систем по функционированию их компонент, правила построения сложных управляющих систем).