рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Философия
- /
- Сферичні координати
Реферат Курсовая Конспект
Сферичні координати
Сферичні координати - раздел Философия, 15. Формула Гріна. 17. Поверхневий інтеграл I роду; Обчислити його. 18.Криволінійний інтеграл 2 роду; обчислення. 19.Теорема про рівність нулеві криволінійного інтеграла 2 роду по простому замкненому контуру. Положення Точки M(X,y,z) Можна Однозначно Задати Числами ρ,θ,φ...
Положення точки M(x,y,z) можна однозначно задати числами ρ,θ,φ, де ρ – довжина радіус-вектора точки М, φ – кут, який утворює з віссю Ох проекція радіус-вектора точки М на площину Оху, θ – кут , який утворює радіус-вектор точки М з віссю Оz. Числа ρ,θ,φ називаються сферичними координатами точки М. Сферичні координати ρ,θ,φ зв'язані з декартовими координатами такими співвідношеннями: x = ρsinθcosφ, y = ρsinθsinφ,
z = ρcosθ, при чому 0≤ ρ<+∞, 0≤ θ <π, 0≤ φ<2 π.
Обчислимо якобіан: ∂
I(ρ,θ,φ)= =
=  =
=
= ρ²sinθcos²θ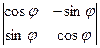 + ρ²sin³θ
+ ρ²sin³θ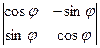 = ρ²sinθ.
= ρ²sinθ.
Використовуючи отримане, запишем формулу: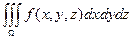 =
=
= 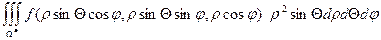 , де ρ²sinθdρdθdφ – елемент об'єму в сферичних координатах.
, де ρ²sinθdρdθdφ – елемент об'єму в сферичних координатах.
28. Криволінійний інтеграл. Маса кривої наближено рівна m =  . Ця сума називається інтегральною сумою для функції f(x,y) на дузі (АВ). Якщо існує границя цієї інтегральної суми при прямуванні λ = max∆Si до 0, то ця границя називається криволінійним інтегралом 1-го роду від ф-ї f(x,y) по кривій L і позначається символом
. Ця сума називається інтегральною сумою для функції f(x,y) на дузі (АВ). Якщо існує границя цієї інтегральної суми при прямуванні λ = max∆Si до 0, то ця границя називається криволінійним інтегралом 1-го роду від ф-ї f(x,y) по кривій L і позначається символом  або
або 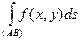 .
.
Отже  =
=
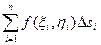 . Поняття криволінійного інтеграла 1 роду по просторовій L:
. Поняття криволінійного інтеграла 1 роду по просторовій L: 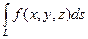 =
= 
 .
.  Обчислення: інтегральна сума криволінійного інтеграла:
Обчислення: інтегральна сума криволінійного інтеграла: 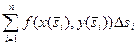 . Цей вираз є інтегральною сумою для визначеного інтеграла:
. Цей вираз є інтегральною сумою для визначеного інтеграла: 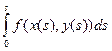 . Одже
. Одже  = (R)
= (R) 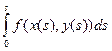 . Зробивши заміну змінної в правій частині цієї рівності отримаємо формулу для обчислення криволінійного інтеграла 1-го роду:
. Зробивши заміну змінної в правій частині цієї рівності отримаємо формулу для обчислення криволінійного інтеграла 1-го роду:  =
=  (1). Якщо крива L задана рівнянням у = ψ(х), а≤х≤b, φ(х) – неперервно диференційована функція на відрізку [а,b], то взявши х за параметр, формула(1) буде виглядати:
(1). Якщо крива L задана рівнянням у = ψ(х), а≤х≤b, φ(х) – неперервно диференційована функція на відрізку [а,b], то взявши х за параметр, формула(1) буде виглядати:  =
= . Якщо L-просторова крива: x=x(t), y=y(t), z=z(t), λ≤t≤β, де x(t), y(t), z(t) – неперервно диференційовані функції на відрізку [λ,β]. f(x,y,z) – неперервна на кривій L, то
. Якщо L-просторова крива: x=x(t), y=y(t), z=z(t), λ≤t≤β, де x(t), y(t), z(t) – неперервно диференційовані функції на відрізку [λ,β]. f(x,y,z) – неперервна на кривій L, то
 =
= 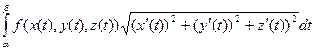 .
.
29. Означення Кратного інтегралу Рімана
Нехай Функція f(x) визначена на вимірній за Жорданом множині G, а T - розбиття множини  . візьмемо на кожній множині
. візьмемо на кожній множині 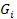 точку
точку 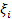 . Вираз
. Вираз 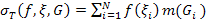
Називають інтегральною сумою Рімана для функції f(x) на множині G , що відповідає розбиттю T і вибірці  точок
точок 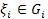 .
.
Означення. Число I називається границею інтегральної суми 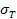 при дрібності
при дрібності 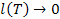 , якщо
, якщо  таке, що для довільного розбиття T з дрібністю
таке, що для довільного розбиття T з дрібністю  і довільної вибірки
і довільної вибірки 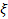 виконується нерівність
виконується нерівність

При цьму пишуть 
Число I називають кратним інтегралом Рімана від функції f(x) на множині G, а функцію – інтегрованою на множині G.
Для кратного інтеграла Рімана використовують позначення

При n=1 маємо визначений інтеграл.
При n=2 інтеграл називають подвійним інтегралом, при n=3 - потрійним інтегралом. Відповідно позначають ці інтеграли

Де D - область на пл.Oxy.
V - деяка обмежена замкнена множина в прямокутній сист. координат Oxyz.
30. Поверхневий інтеграл II роду і його обчислення
Нехай задана проста поверхня 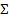 :
:
x= , y=
, y= z=
z=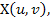
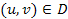 , і нехай в деякому околі поверхні
, і нехай в деякому околі поверхні 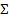 задано неперервне векторне поле, тобто визначена вектор-функція
задано неперервне векторне поле, тобто визначена вектор-функція
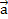 (x,y,z) =P(x,y,z)
(x,y,z) =P(x,y,z)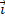 +Q(x,y,z)
+Q(x,y,z)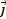 +R(x,y,z)
+R(x,y,z) .
.
Функції P,Q,R є неперервними в деякій області, що містить поверхню 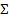 . Орієнтуємо поверхню одиничними нормалями
. Орієнтуємо поверхню одиничними нормалями
 =
=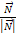 ,
, 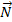 =[
=[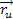 ,
, ] (1)
] (1)
Протилежна орієнтація поверхні  виникає при зміні в формулі (1) вектора
виникає при зміні в формулі (1) вектора 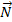 на вектор (-
на вектор (-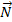 ).
).
Зауважимо, що для простої поверхні 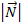


0
Спроектуємо в кожній точці поверхні 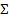 вектор
вектор 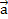 на нормальний вектор. Тоді на поверхні
на нормальний вектор. Тоді на поверхні 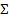 буде визначена неперервна функція F(x,y,z)=(
буде визначена неперервна функція F(x,y,z)=( ,
, ), знак якої залежить від орієнтації поверхні. Потоком вектор-функції
), знак якої залежить від орієнтації поверхні. Потоком вектор-функції 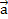 (x,y,z) через орієнтовану поверхню
(x,y,z) через орієнтовану поверхню 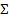 називають поверхневий інтеграл першого роду
називають поверхневий інтеграл першого роду
 (3)
(3)
Перейдемо до інших форм запису інтеграла (3).Нагадаємо, що
 =(
=(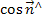 x,
x, 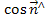 y,
y, 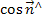 z)=(
z)=(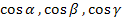 ) (10)
) (10)
Елемент поверхні ds проектується на dxdy елемент площини  (Рис.2)
(Рис.2)
Для достатньо малих ds можна записати 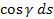 =dxdy.
=dxdy.
Аналогічно можемо записати  ds= dzdx,
ds= dzdx,  ds= dydz
ds= dydz
 =
=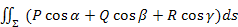 або
або
 =
=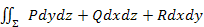 (4)
(4)
Зауважимо, що часто праву частину формули (4) визначають як поверхневий інтеграл ІІроду.
Знайдемо формули обчислення криволінійного інтеграла 4:
 =
= ,
,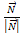 )(
)(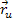 ,
,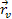 )dudv=
)dudv=  ,
, )dudv
)dudv
– Конец работы –
Эта тема принадлежит разделу:
15. Формула Гріна. 17. Поверхневий інтеграл I роду; Обчислити його. 18.Криволінійний інтеграл 2 роду; обчислення. 19.Теорема про рівність нулеві криволінійного інтеграла 2 роду по простому замкненому контуру.
Формула Гріна... Формула Гріна встановлює зв язок між подвійним інтегралом і криволінійним інтегралом роду...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Сферичні координати
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов