Теорема про неперервність інтеграла, залежного від параметра.

Теорема 2.

Якщо функція 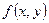визначена і неперервна як функція від двох змінних в прямокутнику , то інтеграл є неперервною функцією від параметра .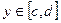

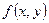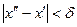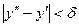○ За теоремою Кантора функція , неперервна на компакті, є рівномірно неперервною на цьому компакті, тобто для , що із нерівностей , слідує нерівність 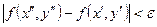. Покладемо 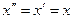, 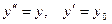. Тоді при 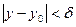для будь-якого маємо 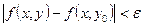, а це означає, що при (прямує) рівномірно відносно . Відповідно за теоремою 1 отримуємо 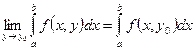, тобто 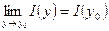, а це означає, що функція є неперервною на відрізку , оскільки 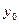– довільна точка цього проміжку. ●

Оскільки функція є неперервною на проміжку , то ця функція є інтегрованою на .

Теорема 2.

Якщо функція 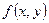є неперервною в прямокутнику , то .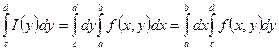

○ Кожен з повторних інтегралів у цій формулі дорівнює подвійному інтегралу від функції 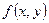на прямокутнику П.●
32. Диференціювання по параметру інтеграла, межі якого залежать від параметра.

Розглянемо інтеграл (1).

Теорема 5.

Нехай функція 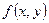визначена і неперервна в області , де 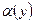, 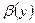– неперервні функції. Тоді інтеграл (1) є неперервною функцією від 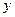на проміжку .

○ Інтеграл (1) можна записати у вигляді 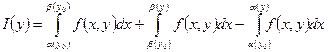(2).

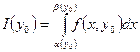Перший інтеграл, в якого межі сталі, при прямує до інтеграла за теоремою 2. Два інші інтеграли (2) допускають оцінки 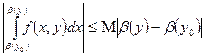, 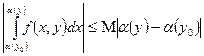(3), де . В силу неперервності функці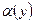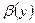й , при інтеграли (3) прямують до нуля. Отже, ●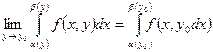

Теорема 6.

Якщо при умовах теореми 5 функція 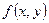має неперервну похідну 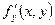, також існують похідні 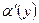, , 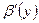то інтеграл (1) має похідну по параметру, яка обчислюється за формулою: (4).

○ Використаємо рівність (2). За теоремою 4 перший інтеграл в точці 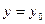має похідну 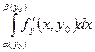(5). Для другого інтеграла рівності (2) значення якого при 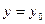є нуль, за теоремою про середнє отримаємо 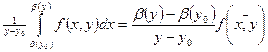, де 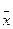міститься між 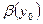і 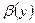. Звідси похідна другого інтеграла при дорівнює 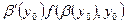(6). Аналогічно для похідної третього інтеграла рівності (2)отримаємо вираз (7). Сумуючи вирази (5), (6), (7) отримаємо формулу (4). ●