Формула Стокса.
Формула Стокса встановлює зв'язок між поверхневим інтегралом і криволінійним інтегралом ІІ роду по кривій, що оточує цю поверхню. Нехай задана гладка поверхня 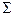 . Позначимо символом
. Позначимо символом  межу цієї поверхні. Виберемо додатну орієнтацію поверхні, тобто якщо дивитися з кінця нормалі, то обхід вздовж кривої
межу цієї поверхні. Виберемо додатну орієнтацію поверхні, тобто якщо дивитися з кінця нормалі, то обхід вздовж кривої  відбувається проти годинникової стрілки. Нормаль
відбувається проти годинникової стрілки. Нормаль 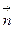 з віссю
з віссю 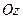 в кожній точці поверхні утворює гострий кут. Нехай
в кожній точці поверхні утворює гострий кут. Нехай 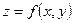 – рівняння простої поверхні
– рівняння простої поверхні 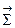 , і на цій поверхні задана неперервно диференційовна функція
, і на цій поверхні задана неперервно диференційовна функція 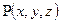 . Оскільки
. Оскільки  і координати контура
і координати контура  задовольняють рівняння
задовольняють рівняння 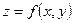 , то значення функції
, то значення функції 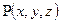 на контурі
на контурі  дорівнюють значенням функції
дорівнюють значенням функції  на контурі
на контурі  – проекції на площину
– проекції на площину 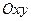 контура
контура  . Отже,
. Отже,  (1). До правої частини рівності (1) застосуємо формулу Гріна:
(1). До правої частини рівності (1) застосуємо формулу Гріна: 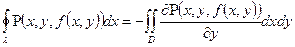 (2). За формулою диференціювання складної функції отримаємо:
(2). За формулою диференціювання складної функції отримаємо: 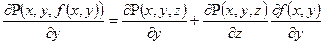 (3). Підставимо праву частину рівності (3) в формулу (2). Тоді
(3). Підставимо праву частину рівності (3) в формулу (2). Тоді 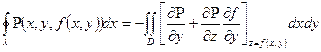 (4). Врахувавши, що
(4). Врахувавши, що  , перетворимо в рівності (4) подвійний інтеграл на поверхневий:
, перетворимо в рівності (4) подвійний інтеграл на поверхневий:  ;
;  . Для поверхні, заданої рівнянням
. Для поверхні, заданої рівнянням 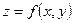 , напрямні косинуси нормалі обчислюються за формулами:
, напрямні косинуси нормалі обчислюються за формулами:  ;
;  ;
;  , де
, де  ,
,  , звідки ми отримуємо
, звідки ми отримуємо  (6). Використавши (5), (6), з рівності (4) отримаємо
(6). Використавши (5), (6), з рівності (4) отримаємо 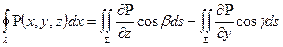 (7). Аналогічно можна отримати формули:
(7). Аналогічно можна отримати формули:  (8),
(8), 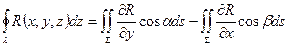 (9), де
(9), де  ,
,  – неперервно диференційовні функції на поверхні
– неперервно диференційовні функції на поверхні 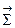 , заданій рівнянням
, заданій рівнянням 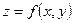 . За формулами (7), (8), (9)можемо записати:
. За формулами (7), (8), (9)можемо записати: 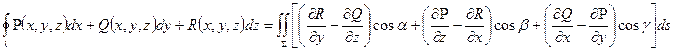 Цю формулу (10) називають формулою Стокса. Позначивши вектор
Цю формулу (10) називають формулою Стокса. Позначивши вектор 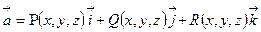 , врахувавши означення циркуляції і потоку векторного поля, суть формули (10) можемо сформулювати в наступній теоремі. Теорема (Стокса). Циркуляція векторного поля
, врахувавши означення циркуляції і потоку векторного поля, суть формули (10) можемо сформулювати в наступній теоремі. Теорема (Стокса). Циркуляція векторного поля 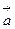 по контуру
по контуру  дорівнює потоку (вихора) вектора
дорівнює потоку (вихора) вектора 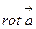 через поверхню
через поверхню 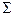 , натягнуту на контур
, натягнуту на контур  , тобто
, тобто 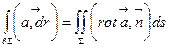 (11) (формула Стокса у векторній формі). Також, врахувавши рівності
(11) (формула Стокса у векторній формі). Також, врахувавши рівності 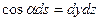 ,
,  ,
,  , формулу (10) можна записати у вигляді:
, формулу (10) можна записати у вигляді: 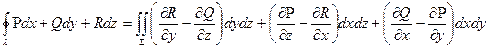 . Зауважимо, що з формули (12) отримаємо формулу Гріна, якщо за поверхню
. Зауважимо, що з формули (12) отримаємо формулу Гріна, якщо за поверхню 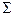 взяти плоску область
взяти плоску область  на площині
на площині 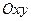 . Справді, поклавши
. Справді, поклавши  , з формули (12) отримуємо
, з формули (12) отримуємо 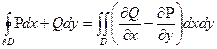 .
.