рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Философия
- /
- Часть I. Последовательности, пределы, производная
Реферат Курсовая Конспект
Часть I. Последовательности, пределы, производная
Часть I. Последовательности, пределы, производная - раздел Философия, Часть I. Последовательности, Пределы, Производная....
Часть I. Последовательности, пределы, производная.
П.1. Числовые последовательности и пределы.
Пусть задано такое множество {c1,c2,¼,c4,¼} пронумерованных действительных чисел, что по номеру элемента мы можем назвать числовое значение данного элемента , а по числовому значению элемента его номер в данном множестве. Тогда говорят, что задана числовая последовательность.
Числовая последовательность обозначается {cn} или просто cn.
Существуют различные способы задания числовых последовательностей.
1) Формулой общего члена cn=(-1)n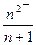 Откуда c1=
Откуда c1=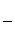
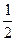 , c2=
, c2=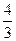 , c3=
, c3=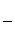
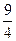 , c4=
, c4=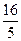 , ¼c100=
, ¼c100=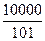 ,¼
,¼
2) перечислением элементов последовательности 1,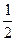 ,
, 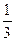 ,
,  ¼ Откуда cn=
¼ Откуда cn=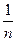
Определение1. Число а называется пределом последовательности {cn}, если
"e>0 $ n0 "n>n0 ½cn-а½<e ( Для любого положительного числа e , существует такой номер n0 , что для всех номеров n>n0 модуль ½cn-а½<e ). Обозначается 
Пример1. cn=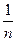 . Покажем , что данная последовательность имеет своим пределом число 0. Пусть e- произвольное число большее 0 ( на самом деле очень малое ). Надо найти такой номер n0, что все элементы cn0+1, cn0+2, ¼, cn0+k,¼(т.е. n>n0 ) удовлетворяют условию ½cn-а ½< e (cn=
. Покажем , что данная последовательность имеет своим пределом число 0. Пусть e- произвольное число большее 0 ( на самом деле очень малое ). Надо найти такой номер n0, что все элементы cn0+1, cn0+2, ¼, cn0+k,¼(т.е. n>n0 ) удовлетворяют условию ½cn-а ½< e (cn=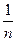 , а=0 ). Решим это неравенство: ½
, а=0 ). Решим это неравенство: ½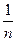 -0 ½<e,
-0 ½<e, 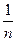 <e, n>
<e, n> , достаточно взять n0= [1/e]- целая часть числа 1/e. Тогда для всех n
, достаточно взять n0= [1/e]- целая часть числа 1/e. Тогда для всех n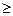 [1/e]+1 неравенство выполняется. Следовательно
[1/e]+1 неравенство выполняется. Следовательно 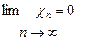
Определение2. Последовательность {cn} называется бесконечно малой, если
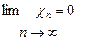 , т.е. "e>0 $ n0 "n>n0 êcn½< e.
, т.е. "e>0 $ n0 "n>n0 êcn½< e.
Определение3. Последовательность {cn} называется бесконечно большой, если
 т.е."E>0 $ n0 "n>n0 ½cn½>E
т.е."E>0 $ n0 "n>n0 ½cn½>E
Пример 2. Последовательности {an}=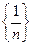 , { bn}=
, { bn}= , {gn}=
, {gn}=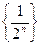 , {dn}=
, {dn}= - бесконечно малые. Здесь n!=1,2,3¼n. 0!=1, 1!=1, 2!=1×2=2, 3!=1×2×3=6, 4!=1×2×3×4=24 и т.д.
- бесконечно малые. Здесь n!=1,2,3¼n. 0!=1, 1!=1, 2!=1×2=2, 3!=1×2×3=6, 4!=1×2×3×4=24 и т.д.
Последовательности {cn}={n}, {yn}={n2},{zn}={2n}- бесконечно большие.
Свойства предела последовательности.
1°. Если  и а > r (а < r), то начиная с некоторого номера хn> r (xn< r).
и а > r (а < r), то начиная с некоторого номера хn> r (xn< r).
Доказательство. Т.к.  , то "e>0 $ n0 "n>n0 ½xn-a ½<e или -e< xn-a <e или а-e< хn<a+e.
, то "e>0 $ n0 "n>n0 ½xn-a ½<e или -e< xn-a <e или а-e< хn<a+e.
Т.е. в e- окрестности точки а ( в интервале ( а-e, а+e )) cодержатся все элементы последовательности , начиная с номера n0+1.
, начиная с номера n0+1.
Пусть а>r. Т.к. e- любое число, положительное, выберем его так, чтобы а-Е было больше r

 а-e
а-e

 r а х ( Можно взять e=
r а х ( Можно взять e= )
)
Тогда " n>n0 r< а-e < хn< a+e, т.е. хn>r. Аналогично для случая а< r.
2°. Если последовательность имеет предел, то он единственный.
3°. Если {хn}={уn}, то 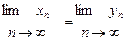
4°. Если хn< уn, то 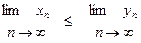
5°. Если хn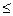 уn, то
уn, то 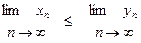
6°. ( Лемма о двух милиционерах ) Пусть хn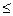 уn
уn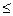 zn (или хn< уn< zn ),
zn (или хn< уn< zn ),  ,
,
Тогда последовательность уn имеет предел 
Доказательство. Т.к.  , то "e< 0 $ n1 "n>n1 a-e< xn< a+e (1)
, то "e< 0 $ n1 "n>n1 a-e< xn< a+e (1)
Т.к.  , то "e>0 $ n2 "n>n2 a-e< zn < a+e (2).
, то "e>0 $ n2 "n>n2 a-e< zn < a+e (2).
Пусть n0=max {n1, n2 }, тогда " n>n0 выполнено и неравенство (1) и неравенство (2), т.е." n>n0 a-e<xn£ уn£ zn< a+e, т.е. a-e< уn<a+e, т.е. 
Теорема 1. 1.(Связь между сходящимисяи бесконечно малыми)Последовательность {an}- бесконечно малая тогда и только тогда, когда последовательность 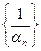 - бесконечно большая ( схематически это будет означать
- бесконечно большая ( схематически это будет означать 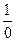 =¥).
=¥).
2. Последовательность {xn}- бесконечно большая тогда и только тогда, когда последовательность  -бесконечно малая (схематически
-бесконечно малая (схематически 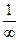 =0).
=0).
Определение4. Последовательность{xn} называется сходящейся, если она имеет конечный предел , последовательность{xn} называется расходящейся если она не имеет предела или её предел равен ¥. Говорят, что сходящаяся последовательность сходится к числу 
Теорема2.Последовательность{xn} является сходящейся (сходится к числу а) тогда и только тогда, когда последовательность {хn-a}-бесконечно малая.
Из этой теоремы получаем, если  , то a-xn=an, где an- бесконечно малая, тогда а=хn+an. Т.е.
, то a-xn=an, где an- бесконечно малая, тогда а=хn+an. Т.е.  Û a=xn+a,где an-бесконечно малая.
Û a=xn+a,где an-бесконечно малая.
Теорема3. (арифметические операции над сходящимися последовательностями)
Пусть  ,
, 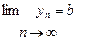 , тогда
, тогда
1. 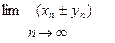 =a±b
=a±b
2. 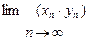 =a×b
=a×b
3. при b¹0  =
=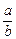
П.2 Предел функции.
Определение1. Число а называется пределом функции у=f(х), при х стремящемся к х0 (), если для любой последовательности{xn} сходящейся к x0… Из определения 1 следует, что для предела функции справедливы все теоремы,… Определение2. Число а называется пределом функции у=f(x) при х стремящимся к х0 (),если "e>0 $ d>0 "х…П.3 Определение производной. Таблица производных.
Определение1. Пусть у=f(x)-произвольная функция, х0-значение аргумента получило приращение
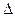 х и стало равным х.
х и стало равным х. 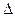 х=х-х0 (приращение может быть отрицательным), тогда функция изменила своё значение с у0=f(x0) до y1=f(x1),т.е. функцияy=f(x) получила приращение
х=х-х0 (приращение может быть отрицательным), тогда функция изменила своё значение с у0=f(x0) до y1=f(x1),т.е. функцияy=f(x) получила приращение 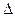 у=
у=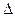 f(x)=f(x)-f(x0). Если существует конечный предел
f(x)=f(x)-f(x0). Если существует конечный предел 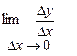 , то он называется производной функции в точке х0.
, то он называется производной функции в точке х0.
Из определения производной и теоремы о связи между сходящейся и бесконечно малой следует
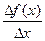 =f¢(x0)+a(x), где a(x)®0 при
=f¢(x0)+a(x), где a(x)®0 при 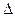 x®0 или
x®0 или 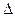 f(x)=f¢(x0)
f(x)=f¢(x0)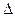 x+a(x)
x+a(x)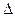 x (1)
x (1)
Определение2. Функция f(x) непрерывна в точке х0, если 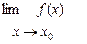 =f(x0) (2)
=f(x0) (2)
Из (1) следует что если функция имеет производную в точке х0, то она в этой точке непрерывна.
Теорема 1.Сумма, разность, произведение 2-х функций, непрерывных в точке х0, непрерывно в точке х=х0. Частное 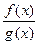 двух непрерывных в точке х0 функций непрерывно в точке х0, если g(x0)¹0 .
двух непрерывных в точке х0 функций непрерывно в точке х0, если g(x0)¹0 .
Доказательство этой теоремы следует из теоремы об арифметических операциях над сходящимися последовательностями (функциями) и определения непрерывной функции (формула(2)).
Определение3. Пусть даны две функции у=f(u) и U=Y(x), y=F(x)=f(Y(x)) называется их суперпозицией (у=F(x) называется сложной функцией).
Пример1. y=cosx2, y=cosu, u=x2,
y=etgx y=eu u=tgx
Теорема2.(о производной сложной функции)
Пусть у=f(u) и u=Y(x) имеют производные в точках u0 и х0 соответственно, причём u0=Y(x0), то y=F(x)=f(Y(x)) имеет производную в точке х0 и
F¢(x0)=f(Y(x0))¢=f¢(u0)Y¢(x0).
Доказательство. Из(1) Df=f¢(u0)Du+a1(u)Du, (4)
DY=Y¢(x0)Dx+a2(x)Dx, (5)
a1(u)-бесконечно малая при Du®0, a2(х)-бесконечно малая при Dх®0
Т.к. функция u=Y(x) имеет производную в точке х0, то Y(x) непрерывна в точке х0, следовательно при Dх®0 Du=DY(x)®0,т.е.a1(u) будет бесконечно малой при Dх®0.
Разделим (4) на Dх, получим 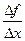 =f¢(x0)
=f¢(x0)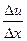 +a1(u)
+a1(u)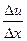 , u=Y(x), значит
, u=Y(x), значит
 =f¢(x0)
=f¢(x0)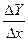 +a1(Y)
+a1(Y)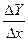 .
.
Перейдём к пределу при Dх®0
lim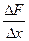 =F¢(x)=f¢(u0)lim
=F¢(x)=f¢(u0)lim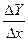 +lima1(Y)
+lima1(Y)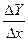 =f¢(x0)Y¢(x0)+0=f¢(x0)Y¢(x0).
=f¢(x0)Y¢(x0)+0=f¢(x0)Y¢(x0).
Определение4. Пусть у=f(x) определена, непрерывна и строго убывает (возрастает) в некоторой окрестности точки х0, тогда существует функция х=f -1(y)- которая называется обратной к у=f(x) в некоторой окрестности точки у0=f(x0), при этом f(f-1(y))=y, f-1(f(x))=x.
Теорема3.(Производная обратной функции).
Пусть у=f(x) имеет производную в точке х0, и х=f-1(y)- обратная к y=f(x0), тогда функция х=f-1(у) имеет обратную в точке у0=f(x0) и(f-1(y0)¢=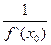
Дифференцированием будем называть процесс нахождения производной.
Теорема.(правила дифференцирования).
1) (C)¢=0 2) (U(x)±V(x))¢=U¢(x)±V¢(x) 3)(U(x)×V(x))¢=U¢(x)V(x)+U(x)V¢(x)Геометрический смысл производной.
Рассмотрим функцию у=f(x) определённую на отрезке [a,b]. Пусть А(х0,f(x)) и B(x+x0, f(x0+Dx))- две точки на кривой у= f(x).Теорема1.(теорема Ферма).
Пусть f(x) определена и непрерывна в некоторой окрестности точки х0, достигает максимума или минимума в точке х0 Î(a,b) и имеет конечную f`(x0), то f`(x0)=0.
Доказательство.
Допустим в точке х0- максимум(т.е. наибольшее значение из всех возможных значений для х из данной окрестности), тогда "х из этой окрестности f(x)<f(x0).
Рассмотрим 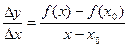 , пусть х<х0, тогда f(x)<f(x0), т.е. f(x)-f(x0)<0, x-x0<0, т.е.
, пусть х<х0, тогда f(x)<f(x0), т.е. f(x)-f(x0)<0, x-x0<0, т.е.
 >0 (1), при х>х0 аналогично получаем
>0 (1), при х>х0 аналогично получаем  <0 (2). Тогда перейдём к пределу в неравенствах (1) и (2) при Dх®0. Из (1) следует, f`(x0)=
<0 (2). Тогда перейдём к пределу в неравенствах (1) и (2) при Dх®0. Из (1) следует, f`(x0)= 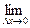
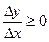 , из (2) f`(x0)=
, из (2) f`(x0)=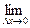
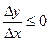 .Отсюда f`(x0)=0. Аналогичные рассуждения для случая минимального значения f(x0).
.Отсюда f`(x0)=0. Аналогичные рассуждения для случая минимального значения f(x0).
Теорема2.(теорема Ролля).
Если f(x) определена и непрерывна на [a,b], имеет конечную производную в (a,b), f(a)=f(b), то существует точка с Î(a,b), что f(c)=0.
Доказательство.
По 2-ой теореме Вейерштрасса f(x) достигает на [a,b] cвоего наибольшего М и наименьшего m значений.
а) М=m, тогда f(x)=const на [a,b], т.е. f`(x)=0 "xÎ[a,b] и теорема доказана.
б) М¹m, тогда так как f(a)=f(b), то по крайней мере одно из М и m достигается внутри (a,b), т.е.$ с, где f(c)=m,т.е. в точке с- минимум, тогда по теореме Ферма f`(c)=0
Теорема3.(Лагранжа).
Если f(x) определена и непрерывна на [a,b] и имеет конечную производную в (a,b), то $ cÎ(a,b), что f(a)-f(b)=f`(c)(a-b).
Доказательство.
Введём вспомогательную функцию Y(x)=f(x)-f(a)-
Эта функция определена и непрерывна на [a,b], дифференцируема на (a,b), Y(a)=0=Y(b).
Т.е. Y(x) удовлетворяет теореме Ролля. Тогда $cÎ[a,b] Y`(c)=0
Y`(x)=f`(x)-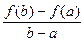 , иY(c)=f`(c)-
, иY(c)=f`(c)-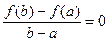
f`(c)=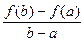 , т.е. f(b)-f(a)=f`(c)(b-a).
, т.е. f(b)-f(a)=f`(c)(b-a).
Теорема4.(теорема Коши).
. Доказательство.Линейная замена переменной.
Доказательство. Пусть ax+b=t (замена переменной) dt=(ax+b)`dx dt=adx, dx= Тогда– Конец работы –
Используемые теги: часть, последовательности, Пределы, Производная0.073
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Часть I. Последовательности, пределы, производная
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов