Уравнение прямой и плоскости в пространстве
Общим уравнением плоскости называется уравнение
 , (3.6)
, (3.6)
полученное из уравнения плоскости, проходящей через данную точку  перпендикулярно данному вектору
перпендикулярно данному вектору  :
:
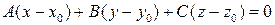 . (3.7)
. (3.7)
Уравнение плоскости, проходящей через три заданные точки: 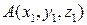 ,
,  ,
, 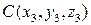 имеет вид:
имеет вид:
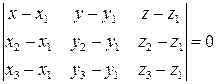 . (3.8)
. (3.8)
Каноническими уравнениями прямой в пространстве называют уравнение
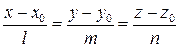 . (3.9)
. (3.9)
Геометрический смысл канонических уравнений прямой заключаются в том, что они описывают прямую, проходящую через точку  параллельно вектору
параллельно вектору  , который называется направляющим вектором прямой.
, который называется направляющим вектором прямой.
Пример 3.6. Даны координаты вершин A(3;–2;–4), B(–5;3;4), C(1;–3;2), D(4;1;–2) пирамиды ABCD. Найти: а) уравнение прямой АВ, б) уравнение плоскости АВС.
Решение. Найдем координаты векторов 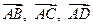 :
:
 .
.
а) Для того чтобы найти уравнение прямой AB, воспользуемся формулой прямой, проходящей через две точки:
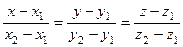 . (3.10)
. (3.10)
Подставим координаты точек A и B:
 , или
, или  .
.
б) Для того чтобы найти уравнение плоскости ABC, воспользуемся формулой (3.8). Подставим координаты точек A, B и C:
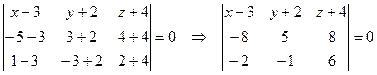 .
.
Вычислим этот определитель, разлагая его по первой строке:
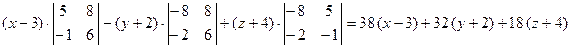
Раскрывая скобки и приравнивая нулю полученное выражение, получим уравнение искомой плоскости:
 ,
,
или
 .
.
Пример 3.7. Составить канонические уравнения прямой, заданной общими уравнениями:
L: 
Решение. Чтобы составить канонические уравнения прямой, нужно знать какую-либо точку на этой прямой и какой-либо направляющий вектор. Найдем координаты точки. Для этого нужно найти общее решение данной системы двух уравнений, а затем выбрать какое-либо частное решение. Мы поступим несколько иначе, сразу выберем частное решение, для этого придадим какой-либо переменной числовое значение. Тогда останется только две переменные и система станет определенной. Решая полученную систему, найдем числовые значения оставшихся переменных, а, следовательно, и координаты точки на заданной прямой. Пусть x=0, тогда система примет вид:
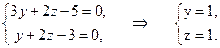
Таким образом, M(0,1,1)ÎL. В качестве направляющего вектора прямой можно взять вектор
 ,
,
где  и
и 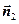 – направляющие векторы плоскостей, входящих в общие уравнения прямой. Так как
– направляющие векторы плоскостей, входящих в общие уравнения прямой. Так как
 ={1;3;2},
={1;3;2},  ={5;1;2},
={5;1;2},
то

Таким образом,
L: 
Пример 3.8. Найти уравнение плоскости, проходящей через две параллельные прямые:
L1:  и L2:
и L2: 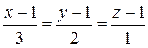 .
.
     L1 L2
M1 L1 L2
M1
 M2 M2
|
Решение. Первая прямая проходит через точку 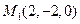 , вторая через точку
, вторая через точку  . Найдем нормальный вектор искомой плоскости:
. Найдем нормальный вектор искомой плоскости:
 .
.
Так как  ={3;2;1}, M1(2;–2;0), M2(1;1;1),
={3;2;1}, M1(2;–2;0), M2(1;1;1),
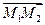 ={–1;3;1}, то
={–1;3;1}, то
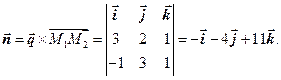
Поскольку M1ÎL, то уравнение искомой плоскости будет иметь вид (см. формулу (3.7)):
P: –1(x–2)–4(y+2)+11z=0 Þ P: –x–4y+11z–6=0.
Пример 3.9. Найти координаты точки пересечения плоскости
P:2x+y–z–4=0 и прямой L: 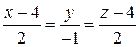 , а также угол между ними.
, а также угол между ними.
         L L
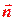 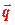 j
P
j
P
|
Решение. Углом между прямой и плоскостью называется угол между прямой и ее проекцией на плоскость. Однако гораздо проще определить угол между векторами 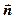 и
и  . Поскольку
. Поскольку
 ,
,
то
|cos( )| = |cos(900 ± j)| = sinj.
)| = |cos(900 ± j)| = sinj.
Отсюда следует формула для определения угла между плоскостью и прямой:
 . (3.11)
. (3.11)
В нашем случае
 = {2;–1;2} и
= {2;–1;2} и 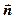 = {2;1;–1}.
= {2;1;–1}.
Тогда
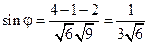 Þ j » 80.
Þ j » 80.
Чтобы найти точку пересечения L и P, нужно решить систему трех уравнений (одно уравнения дает уравнение плоскости и два уравнения дают уравнения прямой). Однако мы поступим по-другому, представив уравнение прямой в параметрической форме:
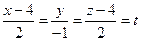 Þ
Þ 
Подставим выражения для x, y и z в уравнение плоскости и найдем после этого параметр t:
2x+y–z–4=0 Þ 2(4+2t)+(–t)–(4+2t)–4=0 Þ t=0.
Найдем значения

которые являются координатами точки M пересечения прямой L и плоскости P:
 = M(4;0;4).
= M(4;0;4).