Кривые второго поряка

Линия – геометрическое понятие, точное и достаточно общее определение которого представляет значительные трудности и осуществляется в различных разделах математики различно. В аналитической геометрии линия на плоскости определяется уравнением F(x,y)=0. Если в декартовой системе координат F(x,y) – многочлен какой-либо степени, то линия называется алгебраической, а степень многочлена – порядком линии. В противном случае, линия называется трансцендентной (например, sinx, lnx и др.).

С алгебраической точки зрения наиболее простыми после линий 1-го порядка (прямых) являются линии 2-го порядка, которые в декартовой системе координат в общем виде описываются многочленом второго порядка:

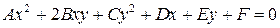. (3.12)

Наиболее простой линией второго порядка является окружность, каждая точка которой равноудалена от некоторой точки, называемой центром. Чтобы задать окружность, нужно знать координаты ее центра C(x₀,y₀) и ее радиус R. Тогда уравнение окружности можно записать в следующем виде:

. (3.13)

Это есть каноническое уравнение окружности.

Эллипсом называется линия, которая в некоторой прямоугольной декартовой системе координат определяется уравнением

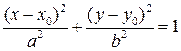(3.14)

при условии a³b. Параметры a и b называются большой и малой полуосями эллипса. Точка C(x₀,y₀) – центром эллипса. Точки F₁ и F₂ – это фокусы эллипса, отстоящие от центра на расстояние 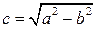, называемое фокальным расстоянием. Число 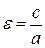(0 £ e < 1) называется эксцентриситетом эллипса и является мерой его «сплюснутости»

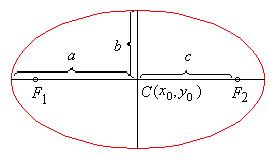
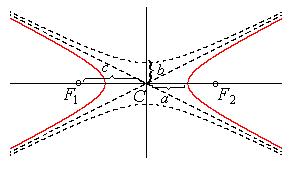
Гиперболой называется линия, которая в некоторой прямоугольной декартовой системе координат определяется уравнением

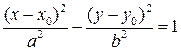(3.15)

Параметры a и b называются действительной и мнимой полуосями гиперболы. Точка C(x₀,y₀) – центром гиперболы. Точки F₁ и F₂ – это фокусы гиперболы, отстоящие от центра на расстояние , называемое фокальным расстоянием. Уравнения асимптот имеют вид

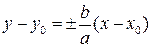. (3.16)

Число 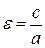называется эксцентриситетом, только в случае гиперболы это число e>1. Если a=b, то гипербола называется равносторонней.

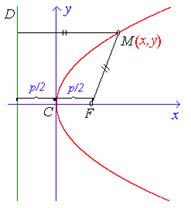Параболой называется линия, которая в некоторой прямоугольной системе координат определяется каноническим уравнением

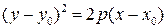. (3.17)

где p>0. Число p называется фокальным параметром параболы, точка C(x₀,y₀) есть вершина параболы, точка F, отстоящая от вершины на расстояние p/2, называется фокусом параболы. Прямая D, перпендикулярная к оси параболы и проходящая на расстоянии p/2 от ее вершины, называется директрисой параболы.

Пример 3.10. Составить уравнение окружности, если известно, что точки A(–7;4) и B(17;–6) являются концами ее диаметра.

Решение. Известно, что центр окружности делит любой диаметр пополам. Поэтому координаты центра окружности находим как координаты точки, делящей отрезок АВ пополам (см. формулу (2.6)):

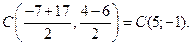
Радиус окружности будет равен половине диаметра АВ (см. формулу (2.5)):

.

Таким образом, уравнение окружности имеет вид (x–5)² + (y+1)² = 13².

Пример 3.11. Вывести уравнение кривой, сумма расстояний от каждой точки которой до двух точек A(–4;0) и B(4;0) есть величина постоянная и равная 10.

Решение. Обозначим через M(x,y) произвольную точку кривой. Запишем геометрическое свойство точек кривой:

|AM| + |BM| = 10.

Распишем это уравнение:

.

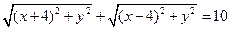Перепишем это уравнение следующим образом:

.

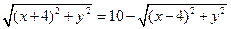Возведем обе части в квадрат:

,

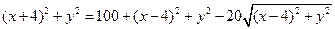после упрощений получим

.

Сократив полученное уравнение на 4, возведем его еще раз в квадрат:

.

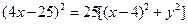Раскроем скобки

16x²–200x+625 = 25x²–200x+400+25y² Þ 9x²+25y² = 225.

Отсюда получаем

.

Это есть каноническое уравнение эллипса.

Рассмотрим уравнение второго порядка:

.

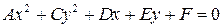Здесь нет смешанного произведения xy. Такое уравнение приводится к каноническому виду при помощи параллельного переноса координат. Аналитически это эквивалентно методу выделения полного квадрата.

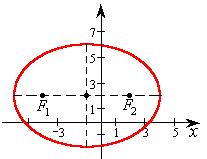
Пример 3.12. Показать, что данное уравнение

16x² + 25y² + 32x – 100y – 284 = 0

определяет эллипс, приведя его к каноническому виду. Найти центр эллипса, его полуоси и эксцентриситет. Сделать чертеж

Решение. Сгруппируем слагаемые, содержащие x и y:

16(x² + 2x) + 25(y²– 4y) – 284 = 0

После этого выражения в скобках преобразуем таким образом, чтобы можно было воспользоваться формулой полного квадрата, т.е. в каждой скобке добавим и отнимем такое число, чтобы можно было воспользоваться формулой: a²+2ab+b²=(a+b)²:

.

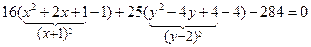Отсюда получаем:

16(x²+1)² – 16 + 25(y²–2)² – 100 – 284 = 0,

или

16(x²+1)² + 25(y²–2)² = 400.

Разделив это уравнение на 400, получим

.

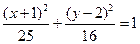Это уравнение – каноническое уравнение эллипса, центр которого находится в точке О(–1,2). Большая полуось равна a=4, малая b=3, фокальное расстояние 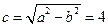, эксцентриситет e=c/a = 4/5.

Пример 3.13. Показать, что уравнение

9x² –16y² + 18x + 64y – 199 = 0

определяет гиперболу, приведя его к каноническому виду. Найти центр гиперболы, ее полуоси, эксцентриситет и уравнения асимптот. Сделать чертеж.

Решение. Дополняя члены, содержащие x и y, до полного квадрата:

9(x²+2x) – 16(y²–4y) – 199 = 0,

или

9(x+1)² – 9 – 16(y–2)² + 64 – 199 = 0.

Отсюда получаем каноническое уравнение гиперболы:

.

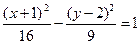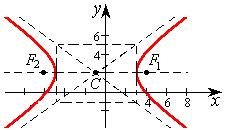Следовательно, центр гиперболы находится в точке С(–1;2), действительная полуось a=4, мнимая b=3, фокальное расстояние , эксцентриситет e=c/a = 5/4. Уравнения асимптот имеют вид

,

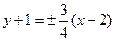или 3x–4y–10 = 0 и 3x+4y–2 = 0.

Построение гиперболы лучше начинать с построения асимптот, а затем уже отмечать вершины, фокусы и другие точки.

Вид уравнения линии зависит не только от вида самой линии, но и от выбора системы координат. Для задания некоторых линий часто используют недекартовы системы координат, поскольку в этих координатах уравнение линии может иметь более простой вид. Большое распространение получила полярная система координат.

Для того чтобы ввести полярную систему координат, нужно задать некоторую точку О, называемую полюсом, и некоторый луч, выходящий из точки О, называемый полярной осью. Тогда любая точка на плоскости однозначно определяется двумя числами (полярными координатами): полярным радиусом r и полярным углом j. Полярный радиус r точки М равен длине радиус-вектора этой точки: , а полярный угол j равен углу между радиус-вектором и полярной осью, если полярную ось вращать против часовой стрелки.

Установим теперь взаимосвязь между полярными и декартовыми координатами. Пусть начало прямоугольной декартовой системы координат находится в полюсе, а положительная полуось абсцисс совпадает с полярной осью. Если точка М имеет декартовы координаты x и y и полярные координаты r и j, то, очевидно, что

x = r cosj, y = r sinj, (3.18)

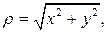
. (3.19)

Уравнение линии в полярной системе координат имеет вид F(r,j)=0 или r=f(j). Для того чтобы соответствие между точками плоскости и полярными координатами было взаимно однозначными, обычно полагают, что r и j изменяются в следующих границах:

0 £ r < +¥, 0 £ j < 2p.

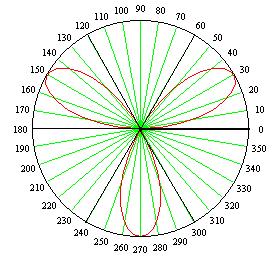
Пример 3.14. Построить кривую, заданную в полярных координатах: r = 4sin3j (трехлепестковую розу).

Решение. Найдем область изменения заданной функции. Поскольку r³0, то и
sin3j ³ 0. Тогда

2pk £ 3j £p+2pk Þ .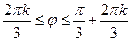

В результате получаем: при k=0 0⁰£j£60⁰, при k=1 120⁰£j£180⁰, при k=2 240⁰£j£300⁰. Таким образом, область определения исходной функции состоит из трех секторов. Поскольку все они равноправны, в силу периодичности синуса, то достаточно построить график только в одном секторе.

j		100	150	200	300	400	450	500	600
r

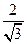
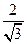
В итоге получаем следующий график трехлепестковой розы: