Определители
Определитель есть число, полученное из элементов матрицы A и характеризующее её. Матрицы обычно обозначаются символами: det A, |A| или D..
|
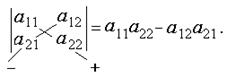
Он равен произведению элементов главной диагонали матрицы минус произведение элементов второй диагонали. Например:
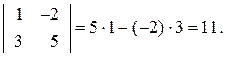
Определитель матрицы 3-го порядка находится следующим образом
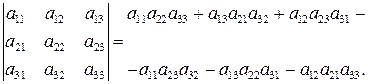 (1.2)
(1.2)
Естественно, что запомнить эту формулу довольно трудно. Однако есть правила, которые облегчают выписывание выражения для определителя 3-го порядка. Например,
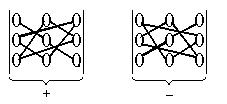 Правило треугольников: три слагаемых, входящих в исходное выражение со знаком плюс, есть произведения элементов главной диагонали или треугольников, основания которых параллельны этой диагонали. Остальные три слагаемых, входящие со знаком минус, находятся таким же образом, но относительно второй диагонали.
Правило треугольников: три слагаемых, входящих в исходное выражение со знаком плюс, есть произведения элементов главной диагонали или треугольников, основания которых параллельны этой диагонали. Остальные три слагаемых, входящие со знаком минус, находятся таким же образом, но относительно второй диагонали.
Пример 1.3. Вычислить определитель
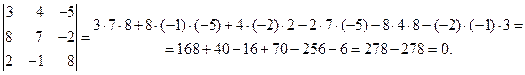
Дополнительным минором Mij элемента aij называется определитель, получаемый из данного путем вычеркивания i-й строки и j-го столбца. Алгебраическим дополнением Aij элемента aij называется минор этого элемента, взятого со знаком (–1)i+j, т.е. Aij = (–1)i+jMij.
Используя понятие алгебраического дополнения можно сформулировать теорему о разложении определителя n-го порядка по строке или столбцу.
Теорема. Определитель матрицы A равен сумме произведений всех элементов некоторой строки (или столбца) на их алгебраические дополнения:

Данная теорема лежит в основе одного из основных методов вычисления определителей, т.н. метода понижения порядка.
Свойство 1. Определитель не изменится, если в нем поменять местами строки и столбцы, т.е. при транспонировании матрицы:
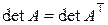 .
.
Данное свойство свидетельствует о равноправии строк и столбцов определителя. Иначе говоря, любое утверждение о столбцах определителя справедливо и для его строк и наоборот.
Свойство 2. Определитель меняет знак при перестановке двух строк (столбцов).
Свойство 3. Если определитель имеет две одинаковые строки (столбца), то он равен нулю.
Свойство 4. Общий множитель всех элементов какой-либо строки (столбца) можно вынести за знак определителя.
Например:
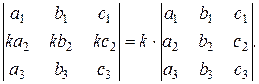
Свойство 5. Если все элементы некоторой строки (столбца) определителя равны нулю, то и сам определитель равен нулю.
Свойство 6. Определитель не изменится, если к элементам одной строки (столбца), прибавить элементы другой строки (столбца), умноженной на какое-либо число.
Свойство 7. Определитель треугольной матрицы равен произведению элементов, стоящих на главной диагонали:
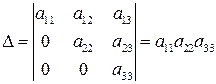 .
.
Пример 1.4. Вычислить определитель:
 .
.
Решение. Упростим данный определитель, а затем вычислим его, разложив его по элементам 2-й строки:
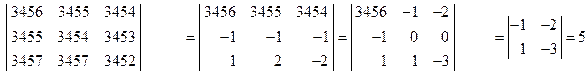 .
.
Пример 1.5. Вычислить определитель:
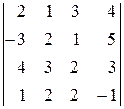 .
.
Решение. Способ 1.При помощи элементарных преобразований матрицы, учитывая свойства определителей, будем получать в какой-либо строке или столбце нули, а затем будем разлагать полученный определитель по этой строке или столбцу:

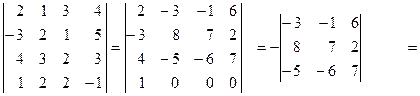
 .
.
 Способ 2.При помощи элементарных преобразований матрицы, учитывая свойства определителей, приведем матрицу к треугольному виду:
Способ 2.При помощи элементарных преобразований матрицы, учитывая свойства определителей, приведем матрицу к треугольному виду:


 .
.